李国强，王显金

（1.贵州财经大学 数统学院，贵州 贵阳 550025；2.重庆大学 数统学院，重庆 401331）

0 引言

在文[1]中，Gromov介绍了度量空间粗嵌入的概念，并指出度量空间粗嵌入到希尔伯特空间或者一致凸巴拿赫空间可能对粗几何Novikov猜测具有重要帮助。随后，在文[2]中，郁国樑证明了具有有界几何的度量空间如果能够粗嵌入到希尔伯特空间，则该空间上的粗Baum-Connes猜测成立，进而粗Novikov猜测也成立。在文[2]中，郁还给出了顺从性的推广形式——性质A，证明了具有性质A的度量空间能够粗嵌入到希尔伯特空间。后来，性质A和粗嵌入得到了广泛的研究。[3-6]在文[4]中，作者证明了性质A在群扩张下的保持性。和性质A不一样，粗嵌入在群扩张下是不稳定的。[7]在文[8]中，Ji，Ogle和W.Ramsey提出了强嵌入的概念，并证明了强嵌入在任何群扩张下都是保持的。

强嵌入也是一种粗几何不变量，它强于粗嵌入又弱于性质A。在文[9]中，J.Xia和X.Wang研究了强嵌入的各种保持性问题和在有限分解复杂度下的不变性；在文[10]中，J.Xia和X.Wang研究了强嵌入在群作用下的遗传性，本文中我们推广了这个结论。

1 准备知识

设X是一个离散度量空间。如果对任意R>0和x∈X，存在NR使得|B(x,R)|≤NR，其中|⋅|表示单位球B(x,R)中元素的个数，则称X具有有界几何。如果存在C>0使得对任意x,y∈X，总有d(x,y)≥C，则称X是一致离散的。在本文中，我们假设所有的度量空间是一致离散的且具有有界几何，这类空间包含许多有趣的例子，比如：有限生成群。设B是一个巴拿赫空间，为了书写方便，我们记B1={η∈B:||η||=1}。对任意R,ε>0，称映射ξ:X→B具有(R,ε)-变差，如果对任意x,y∈X，我们有d(x,y)≤R⇒||ξx-ξy||≤ε。

定义1[8]设X为度量空间，称X是可强嵌入的当且仅当对任意R,ε>0，存在希尔伯特值映射β:X→(l2(X))1满足：

(1)β具有(R,ε)-变差；

由性质A和粗嵌入的等价定义知，强嵌入是介于二者之间的一种粗几何性质，强于粗嵌入而弱于性质A。因此，可强嵌入且具有有界几何的度量空间上的粗Baum-Connes猜测成立。

对一族度量空间来说，我们还经常用到在某种一致控制意义下的强嵌入。

定义2[8]设(Xi)i∈I是一族度量空间，称(Xi)i∈I是等度可强嵌入的，如果对任意R,ε>0，存在一族希尔伯特值映射βi:Xi→(l2(Xi))1满足：

(1)对每个i∈I，βi都具有(R,ε)-变差；

设X是一个集合，ϕi:X→[0,1]是X上的一族连续函数，且满足对任意x∈X，有，则我们称{ϕi}i∈I为X上的一个单位分解。假设U={Ui}i∈I是X的一个覆盖，X上的单位分解{ϕi}i∈I满足对任意i∈I，suppϕi⊆Ui，则我们称{ϕi}i∈I为从属于覆盖U的单位分解。

引理1[10]设X为度量空间，如果对任意R,ε>0，存在X上的单位分解{ϕi}i∈I满足：

(1)对任意x,y∈X，若d(x,y)≤R，则；

(2){ϕi}i∈I从属于X的等度可强嵌入覆盖U={Ui}i∈I，

则X是可强嵌入的。

设U={Ui}i∈I是度量空间X的一个覆盖。对任意x∈X，如果x至多包含在U的k个元素中，则称k为覆盖U的重数。设R>0，对X中任意一个以R为半径的球B(R)，如果B(R)至多与U中的n个元素相交，则称n为覆盖U的R-重数。设L>0，如果X中任意一个半径不超过L的球都能包含在覆盖U的某个元素中，则称覆盖U的勒贝格数为L。如果对任意U′,V′∈U且U′≠V′我们有d(U′,V′)>L，则称覆盖U是L-分离的。

设k≥0,L>0，如果存在覆盖U的一个划分U=U0∪U1∪…∪Uk，且每个Ui，(i=0,1,…,k)是L-分离的，则称覆盖U是(k,L)-分离的。

注意到，如果X的覆盖U是(k,2L)-分离的，则U的L-重数≤k+1。

若令U(L)={x∈X:d(x,U)≤L}，UL={U(L):U(L)∈U}。如果X的覆盖U的L-重数≤k+1，则覆盖UL的重数≤k+1，勒贝格数为L。

定义3[11]设X为度量空间，X具有有限渐近维，如果存在k≥0使得对任意L>0，存在X的一个勒贝格数至少为L、重数为k+1的一致有界覆盖。则满足上述条件的最小的k称为X的渐近维数，记asdimX=k。

引理2[11]设X为度量空间，U={Ui}i∈I是X上重数为k，勒贝格数为L的覆盖。则存在从属于覆盖U的单位分解{ϕi}i∈I使得对任意x,y∈X，有

下面将介绍群的粗拟作用(coarse quasi-action)的概念，它是群的拟作用的推广。[12]

(1)f是恰当的(proper)，如果对Y中任意有界子集B，逆像f-1(B)在X中是有界的。

(2)f是扩张的，如果存在非减函数γ:[0,∞]→[0,∞]使得对任意x,x′∈X，有

(3)如果f既是恰当的又是扩张的，则f称为粗映射。

两个映射f,f′:X→Y被称为相近的(close)，如果存在常数C≥0，使得d(f,f′)≤C。X,Y是粗等价的(coarse equivalent)，如果存在粗映射f:X→Y和粗映射f′:Y→X，使得f∘g和g∘f分别与Y和X上的恒等映射是相近的。

定义5[13]称映射f:G×X→X为群G度量空间X上粗拟作用，如果对每个g∈G，fg:X→X是粗等价映射且满足

(1)所有的fg都是粗映射，且存在非减函数γ:[0,∞]→[0,∞]使得对任意g∈G，有

(2)存在一个数A≥0使得d(fid,idX)≤A；

(3)存在一个数B≥0使得对任意g,h∈G，有d(fg∘fh,fgh)≤B。

玉米淀粉经过挤压蒸煮后，糊化度明显升高，糊化度能达到90%以上。玉米淀粉经过挤压机的挤压和闪蒸后，在室温下冷却，这为RS3的形成提供了条件[9]。滤饼中RS3数量多，则产生的葡萄糖相应减少，影响经济效益，因而需要寻找较优的系统参数组合，使产生的RS3质量分数最少。

从上述定义，我们知道，对任意g∈G，有

2 主要结果

在这一部分，我们将推广文[13]中的结论。首先回顾拟稳定子的概念。设G是一个有限生成群且粗拟作用在度量空间X上，选定X中一点x0。对T>0，群作用的拟稳定子为

另外，我们总是可以把G看成带有字长度量的度量空间。

定理1设G是一个有限生成群且粗拟作用在度量空间X上。如果X具有有限渐近维，且存在X中一点x0使得对任意T>0，拟稳定子WT(x0)是可强嵌入的，则G是可强嵌入的。

证明：

由于轨道Gx0是X的子空间，所以Gx0也具有有限渐近维。不失一般性，我们可以假设G在X上的作用是传递的。

设S是G一个对称有限生成集，d是相对于S的字长度量。令

定义映射π:G→X为π(g)=gx0。如 果G等距作 用在X上，则π:G→X是λ-李普 希茨。但在命 题的条 件下，π:G→X是γ(λ)-李普希茨，其中γ满足定义5(1)。事实上，对任意g∈G和s∈S，我们有

假设asdimX≤k，给出L>0。由定义3知，存在X的一个勒贝格数为L、重数为k+1的一致有界覆盖U={Ui}i∈I，记覆盖U的L-邻域为ν={Vi}i∈I，则ν也是X的一个重数为k+1的覆盖。因为ν是一致有界的，则对任意i∈I，存在T>0和xi∈Xi使得Vi⊆B(xi,T)。

另一方面，我们可取gi∈G使得xi=gi x0。由定义5，我们有d(g-1i xi,x0)≤A+B，

则

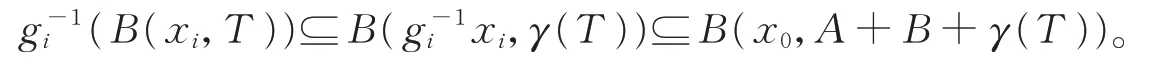
由π:G→X的定义知，

所以我们得到g-1i(Vi)=WA+B+γ(T)(x0)。

注意到{π-1(Vi)}i∈I与WA+B+γ(T)(x0)的一族子空间等距。因为WA+B+γ(T)(x0)是可强嵌入的，则我们有{π-1(Vi)}i∈I是等度可强嵌入的。同理，{π-1(Ui)}i∈I也是等度可强嵌入的且覆盖G。

我们将利用引理1来完成证明。对任意R,ε>0，令L≥。

由于U是X的一个勒贝格数为L、重数为k+1的一致有界覆盖，由引理2知，存在从属于覆盖U的单位分解{ϕUi}Ui∈U满足对任意x,y∈X，有

另外，因为{π-1(Vi)}i∈I是等度可强嵌入的，则存在一族映射βi:π-1(Vi)→(l2(π-1(Vi)))1

使得对任意i∈I，βi具有-变差。对任意i∈I，定义映射φi:G→[0,1]为

下面我们证明{φi}i∈I是G上满足引理1的单位分解。

首先，对任意g∈G，我们有

注意到suppφi⊆π-1(Ui)，则{φi}i∈I是G上的单位分解且从属于覆盖{π-1(Ui)}i∈I。

其次，对任意g,g′∈G,d(g,g′)≤R，如果g∈{π-1(Ui)}i∈I，则存在Ui使得π(g′)∈Ui(γ(λ)R)，其中，Ui(γ(λ)R)是Ui的γ(λ)R-邻域。如果L足够大，则

这样我们有，

由引理1知，G是可强嵌入的。证毕。

因为引理1也适用于粗嵌入到希尔伯特空间和正合性(在具有有界几何度量空间下和性质A等价)，[4]所以对于粗嵌入到希尔伯特空间和正合性具有类似的结论，具体描述如下:

定理2[4]设X为度量空间，如果对任意R,ε>0，存在X上的单位分解{ϕi}i∈I满足：

(1)对任意x,y∈X，若d(x,y)≤R，则；

(2){ϕi}i∈I从属于X的等度可粗嵌入的(等度正合的)覆盖U={Ui}i∈I，

则X是可粗嵌入的(正合的)。

定理3设G是一个有限生成群且粗拟作用在度量空间X上。如果X具有有限渐近维，且存在X中一点x0使得对任意T>0，拟稳定子WT(x0)是可粗嵌入的(正合的)，则G是可粗嵌入的(正合的)。