李效东

（国防科技大学 文理学院，湖南 长沙410073）

长久以来，人们常用一种正规形状（如四方形、矩形、正六边形等）的平面砖无间隙、无重叠地铺设地面或墙面等任意面积的平面F。但是在建筑技术（地砖、墙砖、大型穹顶、互锁砖等）、平面装饰艺术（纺织品、墙纸等）、实用技术（拼接家具木板和地板等）和众多工业领域均希望有多种非正规形状的多边形甚至曲线边缘的平面砖型可供选择。这样不仅可以产生各种不同风格的视觉效果，也可能因为砖间的接触线和接触角的改变而优化工程施工技术和实用性能。此外，平面砖的几何规律和对称性在科学研究中具有重要意义，如可以帮助理解晶体的晶面结构[1-2]以及外延薄膜、分子自组装等现象。

平面砖艺术的产生可追溯到人类的早期文明[3-4]。人们早已发现，有些非规则形状的平面砖可以拼合铺排成如图1-b，c 所示的图案。多年以来，人们不断地发现了许多不同形状的，周期性和非周期性的平面砖型，有的还详细描述了具体多边形平面砖的几何参数。Grünbaum 的专著[5]以巨大的文献量概括了多年来在此领域的研究积累。尽管平面砖的复杂性给系统化描述带来一定的分歧，但仍可进行大致的分类。图2 归纳了不同类型的多边形及其拼合方式。为什么一种看起来本身似乎不具备任何对称性的多边形[6-7]，甚至曲线边缘的平面能够“凑巧”成为平面砖？怎样按照一定的规则设计出不同类型和风格的平面砖？本文的研究目的是探索这些问题的答案。

图1 平面砖及其铺排实例

1 定义

本文提出一类全部边缘可为任意曲线的点阵型平面单砖T，其可以无间隙，无重叠，周期性地铺排成无限大平面F。为了明确概念，本文将曲边T 的讨论范围作以下规定。（1）周期性（periodic），排除图2-a 中的螺旋性[8]，因其不可用平面点阵表示，且铺设平面受限；（2）单形（monohedral），排除图2-b 中的复形，或多种砖形混拼；（3）单面（isohedral），排除图2-c 中的手性双面砖。因地砖、墙砖的正反两面材质不同，手性对映体实际上属于特殊的双形。（4）相邻砖线段全接触（normal），此为曲边啮合的几何要求，故排除图2-d，e 中的线段的非全接触，尽管很多复形和手性对映体也能形成曲边砖，但暂不在此讨论。本文仅限于图2-f 中单形、单面的T。

图2 不同类型的多边形平面砖

无论T 的曲边形状如何复杂，均能以某种凸角多边形（convex polygon）作为基形，在保持基形面积不变的前提下，其直线边按照一定规律曲线化。为数众多的多边形固然可以铺满F，但只有满足一定几何要求的多边形才可以全曲线化而成为T 的基形。

按此定义的边缘可全曲线化的平面砖T 分为“基础平面砖”TE、三种“多重平面砖”TN、TNX和TNX/2。其中TE可以顺着平面上的两个特定方向（或轴）周期性地平移铺排，构成无间隙，无重叠的平面F。多重平面砖必须N 重拼合成一个TE，然后整体平移铺排构成F。

2 基础平面砖TE

根据对称性基本原理[9-10]，任何二维平面砖周期性地扩展形成的无穷大平面F 可视为平面点阵。任何平面点阵均可用元胞（unit cell）表示，而元胞的一般形式为广义的平行四边形P4。因此，所有TE的基形P 必为P4。根据对称性，可将P4按边及夹角分为倾斜Ob（Oblique，A，B，γ）、矩形Rt（Rectangle，A，B，90°）、四方Sq（Square，A，A，90°）、六方Hx（Hexagonal，A，A，120°）和棱形Rb（Rhombus，A，A，γ）。所有P4具有两对平行等长的边偶（Lateral couple，LC），表示为2A2B。

显然，以元胞A，B，γ 定义的点阵内，一个任意有限面积的平面A 如果要成为TE的先决条件必须是：A 边线上任一点p 必须在点阵内具有等效点p（nA，mB），其中n，m 为任意整数。

A 边缘的任何变形将导致其局部的凸出或凹进。为满足以上条件，其对边必须相应地凹进或凸出，相当于一对LC 用完全相同的线替换。此即成为本文定义的TE。因此，将LC 用任意线同替换过程称为“等盈亏”（Equi-Gain-Lose，EGL）操作，形成的新平面称为EGLP。显然，EGLP面积与元胞相同，但形状和对称性完全改变。任何P 可通过EGL 操作实现边缘曲线化。图3 以实例描述了EGL操作及产生的TE。

如P4用折线进行EGLz操作（下标z 表示折线zigzag），如图3-a 所示，则P4变成含凹角的平行4+2n 边形，含有2+n 对LC，可进一步进行任意线的EGL 操作。因为EGLPz的内角无限制，图3-b，c，d 分别显示不同P4经EGLz操作后可以形成三种不同对称性的凸边平行六边形P6（2A2B2C，实际是含一个0°内角的平行八边形）：H2（点群2）、Hm（点群2mm）和H6（点群6mm）。因P6具有特殊的对称性，而且也能顺二轴（三轴中任意二轴）简单平移扩展成F，为方便计算，本文将TE的基形P 定义为P4和P6。

图3 EGLP 构成TE 的实例

不同对称性的P4可通过EGLz操作相互转化。P4[A，B，γ] 可以通过两步EGLz操作转化为面积相同的P4’[A’，B’，γ’]。因为每步只能改变一个轴长，故需引入γ*。

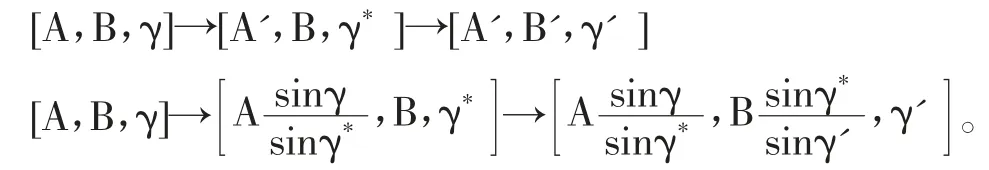
图4 显示了P4相互转化的路线图及按任一路线导致的形状变化。

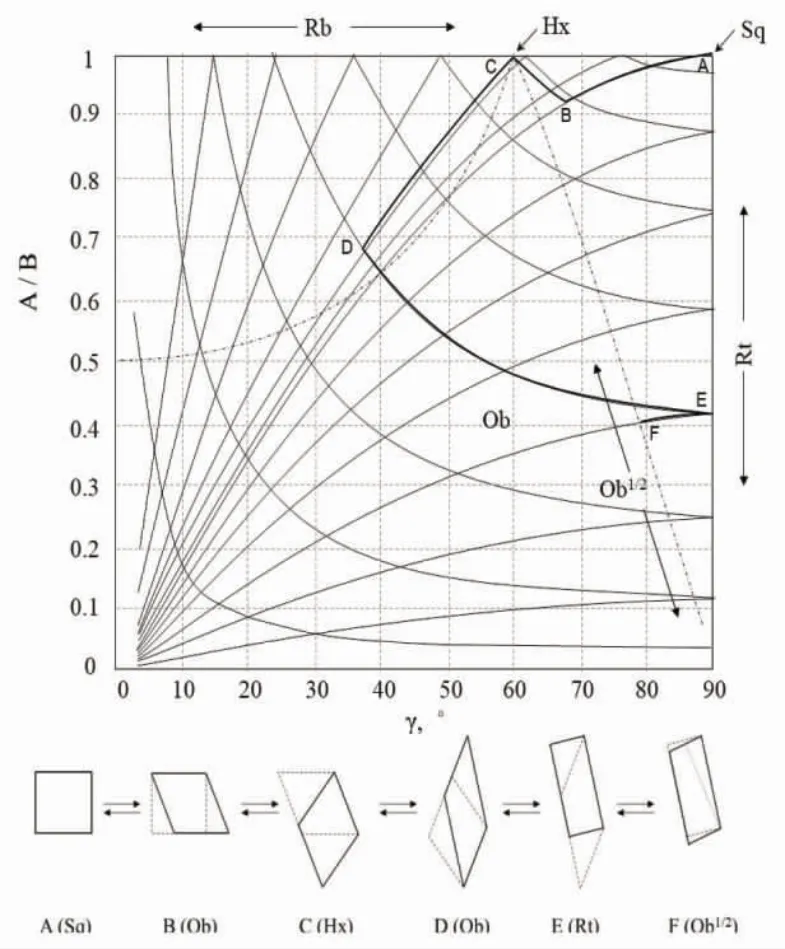
图4 不同的平行四边形P4 通过EGL 操作相互转换路线图

综上所述，可以得到一般的结论：所有EGLP 均为TE；所有的TE必须是EGLP。此外，所有TE均可通过EGL操作相互转化，或者说，同面积的TE构成一个无穷群。

3 TE 的对称性

图5 和图6 通过一些实例，反映出TE对称性的基本概况。

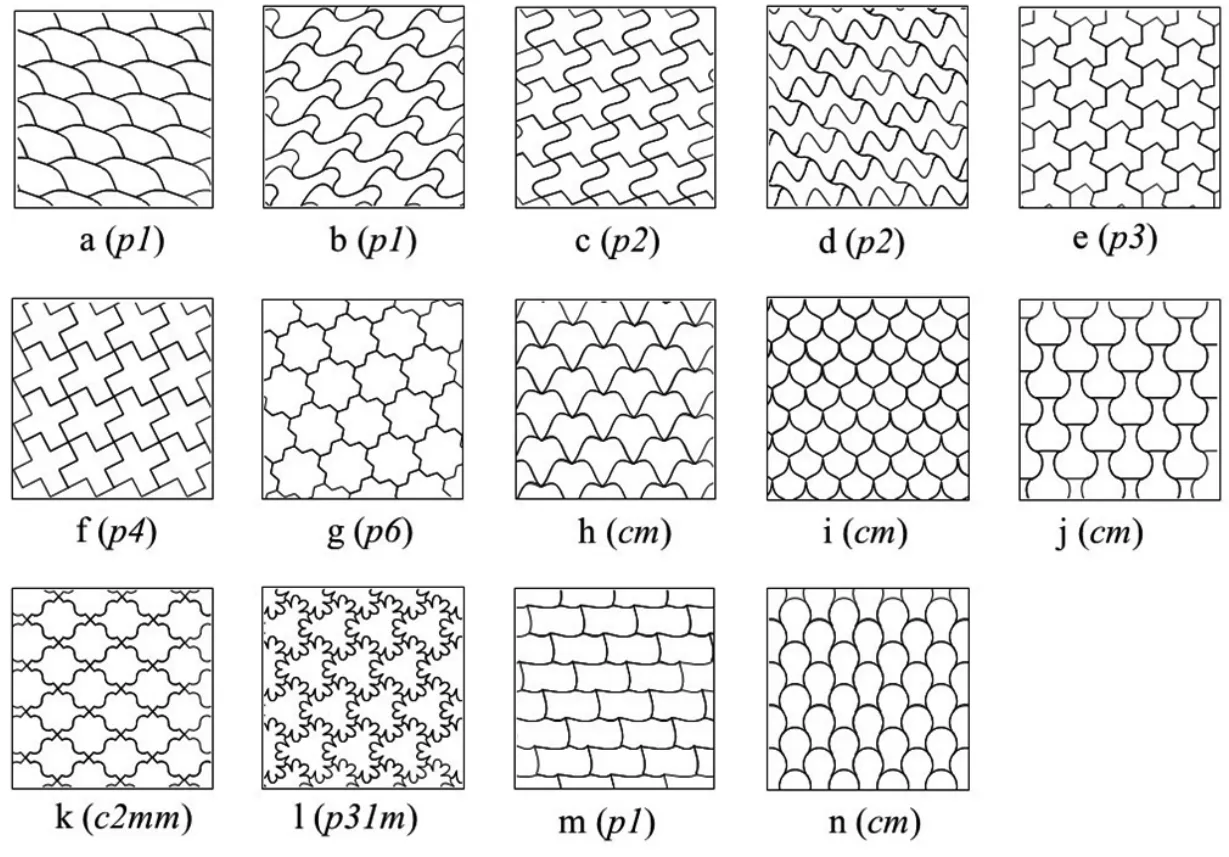
图6 由图5 中的TE 铺排成不同平面群（括弧内）的F

所有的P 均具有旋转轴Cn，有的具有镜面m（Rt、Sq、Hx、Rb、H6、Hm）。P 经过任意线的EGL 操作形成2a2b（2c）（a、b、c 为不交叉的任意曲线，A、B、C 为与以上起点和终点相同的不交叉的折线。等边P 中一般将不同任意线记为a 和a’）后，原则上所有的Cn和m 完全消失，TE的点群降为1，形成的F 的平面群降为p1（图3-a，e，g 和图5，6-a，b，m 为代表）。

如果对EGL 线条进行一定限制，则仍可保留P 的部分对称性。以下为一般规律。

（1）全二重线A（线中点为二重轴）可以保留P 的Cn。如将C2对称的P（Ob、Rt、Hx、Rb、Hm、H2）中的2A2B（2C）替换为2A2B（2C），则可保留C2，形成平面群p2（图5，6-c，d 为代表）；对于C4对称的Sq，4A（2A2A，两组边偶的夹角仍为90°）使其保留C4，形成平面群p4。类似，对于C6对称的H6，6A（2A2A2A，相邻边偶的夹角仍为120°）使其保留C6，形成平面群p6。有趣的是，当采取由直线z 构成的z90°z90°z 的A对Sq 进行4A操作时，EGLP 产生新的m，形成4mm点群。与此相似，z120°z120°z 对H6 进行6A操作时，EGLP 也产生新的m，形成6mm 点群。但这两种情况下，新的m 与原P 的轴不重合，无法带入点阵，故为无效m，铺排成F的点群仍分别为p4和p6（图5，6-f，g）。

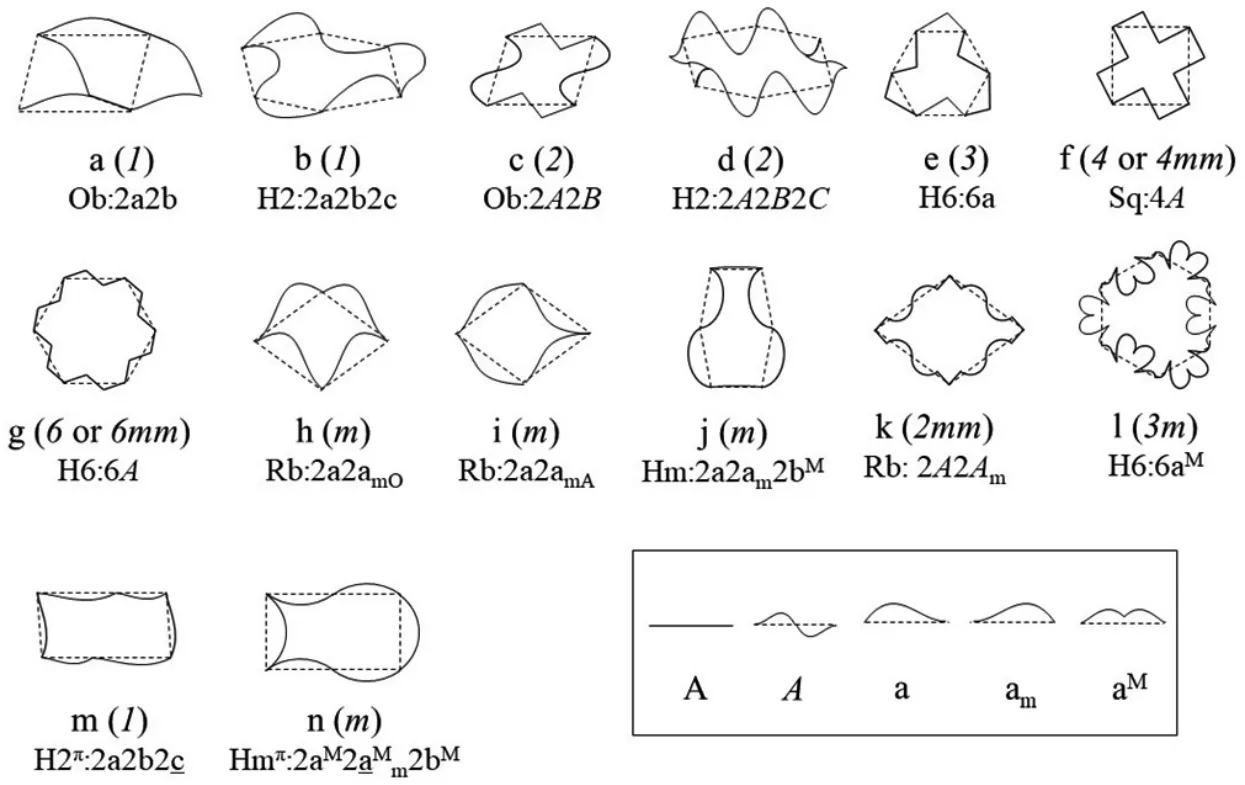
图5 由不同P 和EGL 线条组成的几种典型的TE（标号下方为P 及线条组成，括号内为所属点群）

（2）对三个等轴P4（Sq、Hx、Rb）采取2a2am的EGL 操作可保留一个m。其中Hx 和Rb 根据m 的设置在钝角（o）或锐角（a），有两个异构体（图5，6-h，i）。与此相似，对于Hm，采取2a2am2cM进行EGL 操作也可保留一个m（图5，6-j）。

（3）对三个等轴P4（Sq、Hx、Rb）采取2A2Am的EGL操作，则不仅可保留C2，而且可保留两个相互正交的m，达到高对称性点群2mm，并形成c2mm的F。（图5，6-k为代表）。

（4）H6 为最高对称性的P，即使用任意线进行EGL操作（6a）仍能保留C3（图5，6-e）。当用6aM（aM表示任意线中点为垂直基线的镜面）进行EGL 操作后，则可保留C3和3 个m，形成3m点群和p31m平面群（图5，6-l）。

（5）如果设置两个对称的180°内角，P6缩边为P4。H2可以变成假Ob，记为H2π（图5，6-n）。同样，Hm 可以变为假Rt，记为Hmπ（图5，6-m）。它们的曲线化的一般表示为2a2b2c（下划线b 表示其与前边共线）。缩边P6作为TE形成不同的风格。Hmπ（图5，6-n）可像Hm 一样保留一个m，也可与后述的QRHpm一起描述出矩形砖的多种“错位”砌墙形式。因为0°和180°内角导致的缩边现象，多边形（包括图3-e，f）铺排成F是否全接触并非如图2-d，e那样一目了然。

以上有些TE部分保留了原有的m（图5，6-h，i，j，k，l）或产生新的m（图5，6-f，g）。这些非手性平面砖的正、反面相同。其余的TE均为手性砖，正反面互为对映体。

以上TE囊括了10 个点群，由此可以铺排出具有不同空间群的F。但是因为P 的所有直线被曲线化，所以要求这些直线必须为m 的空间群，如pm、p2mm、p4mm、p6mm、p31m，不会在全曲线化的TE中出现。

4 多重平面砖TN

因为TE是唯一能够仅通过平移而周期性地铺排成F的平面，那么TN必须是TE分割为N 个相同形状的平面之一。P 可能以多种方式均分割为多个凸边多边形。图7 中阴影部分的P 和EGLPz以不同的方式均分割为多个直角正三角形，形成不同的平面群。这些三角形的边缘是否可以全曲线化？什么样的曲线才能够满足要求？

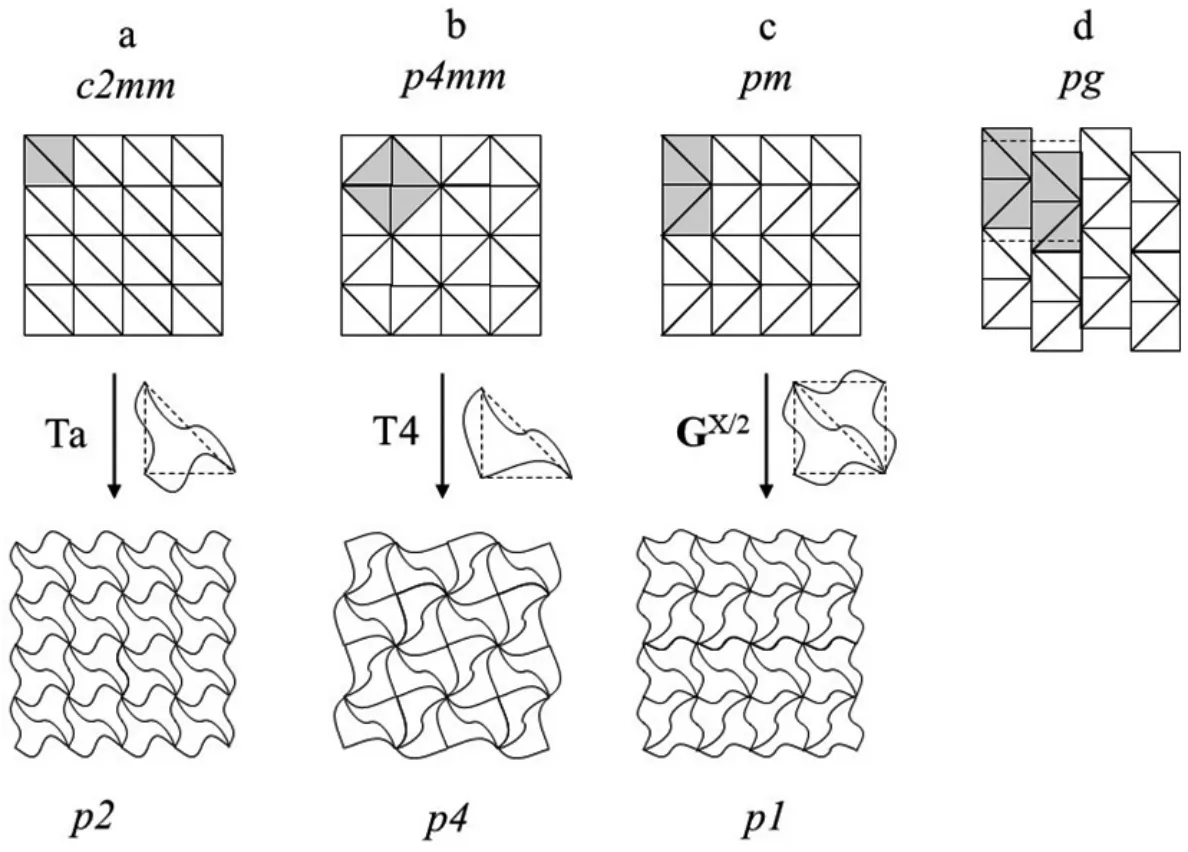
图7 一个P 或EGLPz（阴影部分）被均分割为多个直角等腰三角形的几种方式（其中a、b、c 的三角形可以不同方式（如后述）进行全曲线化；d 为非全接触，不能曲线化）

相邻的TE之间是简单平移等效边。而在一个被分割的P 内，相邻多边形之间则必须是旋转等效边，或者是镜面等效边。图7-a，b 中，分割的P 具有旋转轴，三角形之间分别互为C2（降低的轴次）和C4旋转等效边。分割后三角形的接触边不仅全接触，而且接触边是固定的；而图7-c，d 中，虽然也存在二重轴，但分割线并不全过轴心，导致接触边不固定。但图7c 为全接触，图7d 为非全接触。显然，图7-a，b 中过N 重旋转轴心分割形成的N 个三角形最容易曲线化。

很多EGLPz也可以像P 一样，按照不同的方式均分割为多个特定形状的凸边多边形。要想使这些多边形成为可曲线化的TN，所有相邻多边形也应为旋转等效边。所以EGLPz在分割时应像P 一样保持最低旋转轴，或遵守“过轴心N 分割”的规则。显然，那些具有旋转轴的r-EGLP（r，表示旋转轴rotation）能够成为产生TN的候选者。

因为平面点阵中允许的旋转轴次只能是2、3、4、6，所以N 只能等于2、3、4、6。图8 显示了P 和一些r-EGLPz经“过轴心N 分割”形成凸角x 边形（x=3、4、5、6，分别表示为T，Q，P，H）。显然，这些x 边形可以作为TN的基形G。图8 横线上方为本征G，其基本几何特征用后续的数字或字母表示，如a（arbitrary）表示任意边长和角度；p（parallel）表示有一对平行等长边；数字3，4，6 分别表示相邻的两条等长边之间的夹角为2π/3，2π/4，2π/6。

如前所述，P 具有两对（或三对）平行LC：2A2B（2C），曲线化时同一对LC 必须进行任意线同替换的EGL 操作。从图8 中可以看到，G 也存在曲线化时与等盈亏相关的LC。这些LC 可以是平行的（Qp、Pp、Hp），也可以具有60°、90°、120°夹角，分别记为26A、24A、23A。此外，G 还可能存在独立边（independent lateral，IL，可以单独变化的边），奇边多边形T 和P（x 分别为3 和5）必须具有IL。图7-a 中C2的夹角为180°，故三角形没有LC，三条边A、A、B 均只能作为IL 分别用面积自盈亏的二重线A、A’、B变换。而图7-b 的P 中存在C4，两条90°夹角的等长边为LC（24A），其可以替换为24a，而多余的一条独立边B 用B替换。因此，可将G 的曲线化必须的等盈亏操作（EGLN操作）定义为：LC 在保持夹角的前提下由任意曲线a 进行同替换；IL 由任意二重线A替换。需要强调的是，某一个TN只适合于所产生的P 或EGLPz。如图7 所示，三角形曲线化后只能分别按a、b 的方式原样拼合。

从图8 可见，所有G 中，除了Ta 和Qa 无LC，分别有3 和4 条IL 之外，其余的G 均具有1~3 对LC。按照EGLN操作的规则，每个G 图形下方标明了x 条边对应的一般曲线，或自由度最大的曲线。

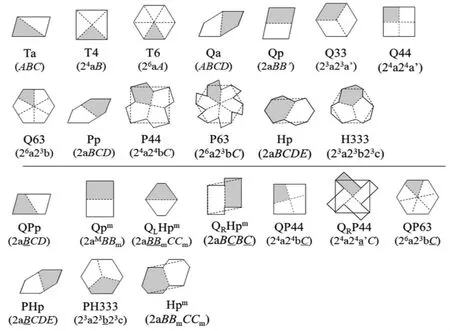
图8 P 或EGLPz 按照“过轴心N 分割”规则得到的多边形G（阴影部分）（横线上部为本征G，下部为衍生G。图形下方为G 的命名，括号内为LC 和IL 及其相应的等盈亏线条）

图9 为本征G 按照EGLN规则曲线化并拼合后铺排形成的F及其空间群。容易判断，图1-c 中曲边砖的基形为H333。因为EGLN操作时均采用一般曲线，不存在含m的点群和空间群。

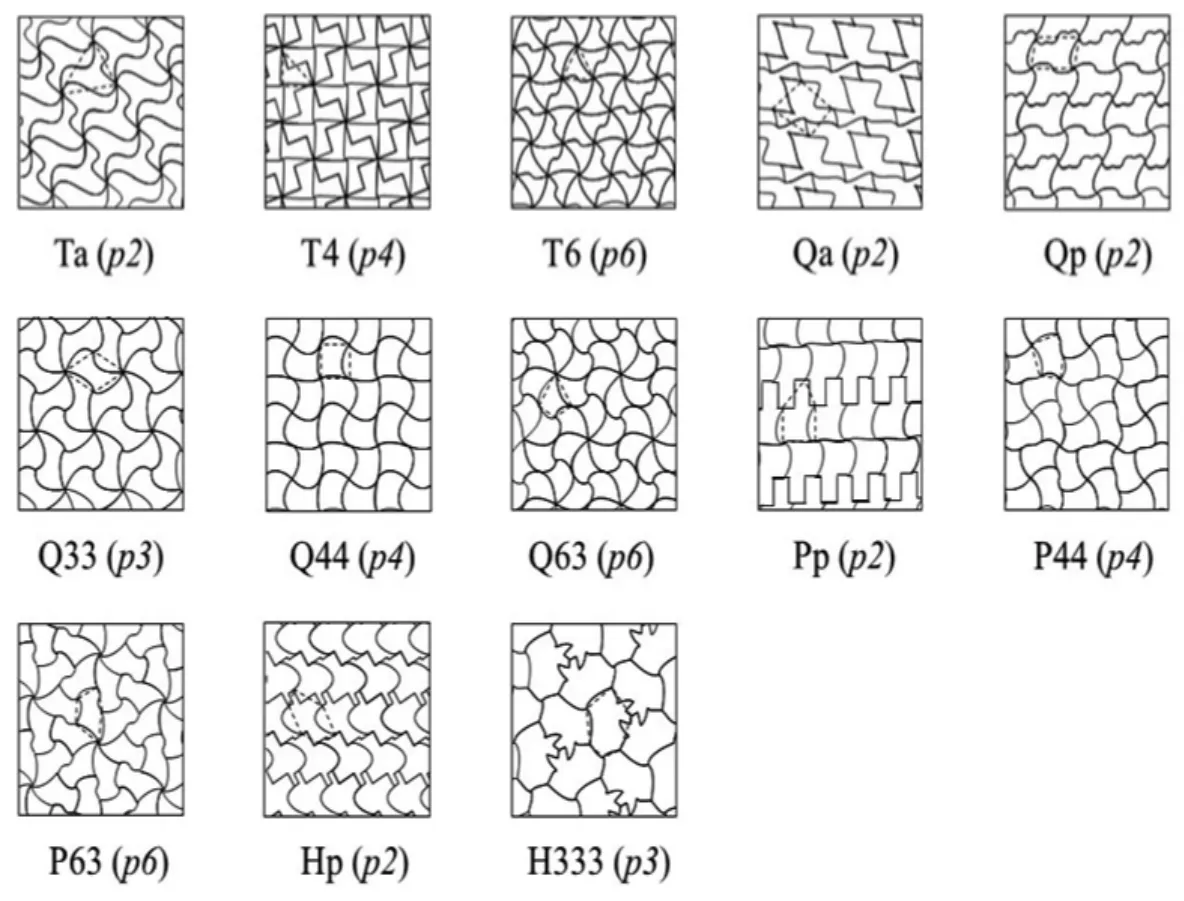
图9 图8 中的本征G 经EGLN 操作得到的TN 及其拼合铺排成的F（括号内为平面群）

图8 横线下方为衍生G，其边的组成与本征G 相同，但其中可能因180°内角导致的缩边，如表观四边形实际为五边形表示为QP；假五实六表示为PH，假四实六表示为QH 等。衍生G 还包含了通过几何限制增加对称性的情况，如通过限制边长和角度，同时将一般曲线改为限制曲线，使Hp 增加一个镜面，变成Hpm等。

还需要特别指出的是，有些G 在满足基本几何关系下可以产生较高对称性，如Pp、P44、H333、PH333 等可能产生m，铺排成高对称性的F。但可惜的是因为存在与m垂直的IL，故EGLN全曲线化操作时，无论对曲线如何限制，这些m 均不可能再存在，故不列入衍生G 清单。图10 为衍生G 经EGLN操作并拼合后铺排形成的F及空间群。其中包括G 的几何形状无变化，仅将一般曲线改为限制曲线后提高了对称性的Q33m（23a23am）、Q44m（24a24am）、Q44mm（4aM）。

G 通过EGLN操作后，面积无变化，LC 和IL 曲线化导致的盈亏部分拼合时正好互补。这样可以形成无穷数量的EGLG。由此得出一般规律：所有EGLG 均可作为TN。

有些TE之间也可以不作为平移等效面，而是作为旋转等效面而构成TN。如Sq（2a2a）与Q44（24a24a，N=4）同形；Hx（2a2amo）与Q33（23a23a，N=3）同形；Hmπ（2aM2aMm2bM）与Qpm（2aMBBm，N=2）同形。还有一些T，既能作为TE，也能作为TN。甚至作为后述的TNX。

在图10 中，除了7 个标明m 的TN之外，均必为手性TN。一般情况下，手性对映体是不可混拼的，只有一些具有特殊线条的EGLG 对映体可以混拼，相当于化学中的外消旋体晶体。因本文的T 仅限单面，故将混拼对映体问题留待以后讨论。

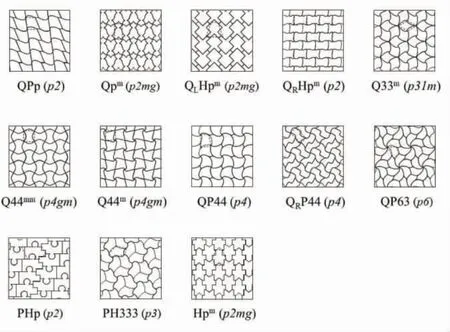
图10 图8 中的衍生G 经EGLN 操作得到的TN 及其拼合铺排成的F（括号内为平面群）

5 等边多重平面砖TNX 和复合等边多重平面砖TNX/2

如同图2-d，e 和图7-d 那样，不（或不能）按照“过轴心N 分割”规则也有可能分割出N’个相同的凸角x 边形。因与轴心无关，N’没有N 的限制。这些任意分割出的多边形既无LC，也无IL，很多是非全接触，表示为GA（上标A 表示Abnormal）。因为GA不可能进行EGLN操作，故不能曲线化。Grünbaum[5]列举了几个极富想象力的凸角五边形或六边形GA。（任意三角形或四边形能够分别以Ta 和Qa 的G 形式拼合并铺排成F）。

导致以上现象的本质是TN在拼合时必须保持绝对的全接触，这需要EGLG 各曲边之间的拼合是固定搭配的：LC 找同样的LC，IL 找同样的IL。“过轴心N 分割”规则可以很好地保证这种固定搭配。而任意分割的多边形并无固定搭配，如不能保证全接触，就不能曲线化。但是，很多等边多边形（Equilateral x-gon，GX）能够实现全接触，故不需要固定搭配，那么“过轴心N 分割”规则就不是必要的了。事实上，x-边形的GX只要是来自P 或者EGLPz，都可以在保持内角不变的条件下用x 个相同的二重线全替换（这是GX曲线化的唯一途径，称为EGLD操作），成为曲边的TNX。图11-a，b，c，d，e 为TNX实例（其中d、e 可视为G6）。

在前述的P 和G 中也有一些GX，如Sq、Rb、Hx、T6（N=6）、Q44（N=4）、Q33（N=3）；边长或角度限制的GX，如Pp（2*90°，60°）、Hm、H2、Hmπ、H2π、P44（2*114.3°，131.4°，N=4）等。它们具有LC，可以引入任意曲线。当然也可以用相同二重线全替换，这与EGL 或EGLN操作的规则是一致的，属于正常的TE或TN。

但是，如图7-c 和图11-f，g，h，i，j 所示，有些P 可以按任意方式分割成多个特殊形状的三角形或四边形，相邻的两个多边形正好拼成一个等边多边形（相当于一个GX再次分割），此即为半等边多边形GX/2。GX/2也可以进行EGLD操作而全曲线化（等长边用相同的二重线替换，分割线为独立边，用单独的二重线替换）。有意思的是，GX/2不必按照分割时的模式原样拼合，而可以多种模式拼合出很多图案，如Sq 作为GX分割为两个直角正三角形（GX/2），经EGLD曲线化后，可以拼合出以图7-c 和图11-f，h 为例的很多种图案。

值得注意的是，一些多边形可以充当多种角色的T。如边长1∶2 的矩形（2mm）。既可视为Rt（2a2b），或者Hmπ（2a2a'2a"）充当TE；也可视为QRHpm（2aBCB'C'）或者QRP44（24a24a'B）充当TN（N 分别为2 和4）；还可以视为等边多边形（G6）充当TNX（N 为大于1 的任意数）构成许多图案，如以图1-b（图11-d，e）等为代表的多种方砖铺地艺术。

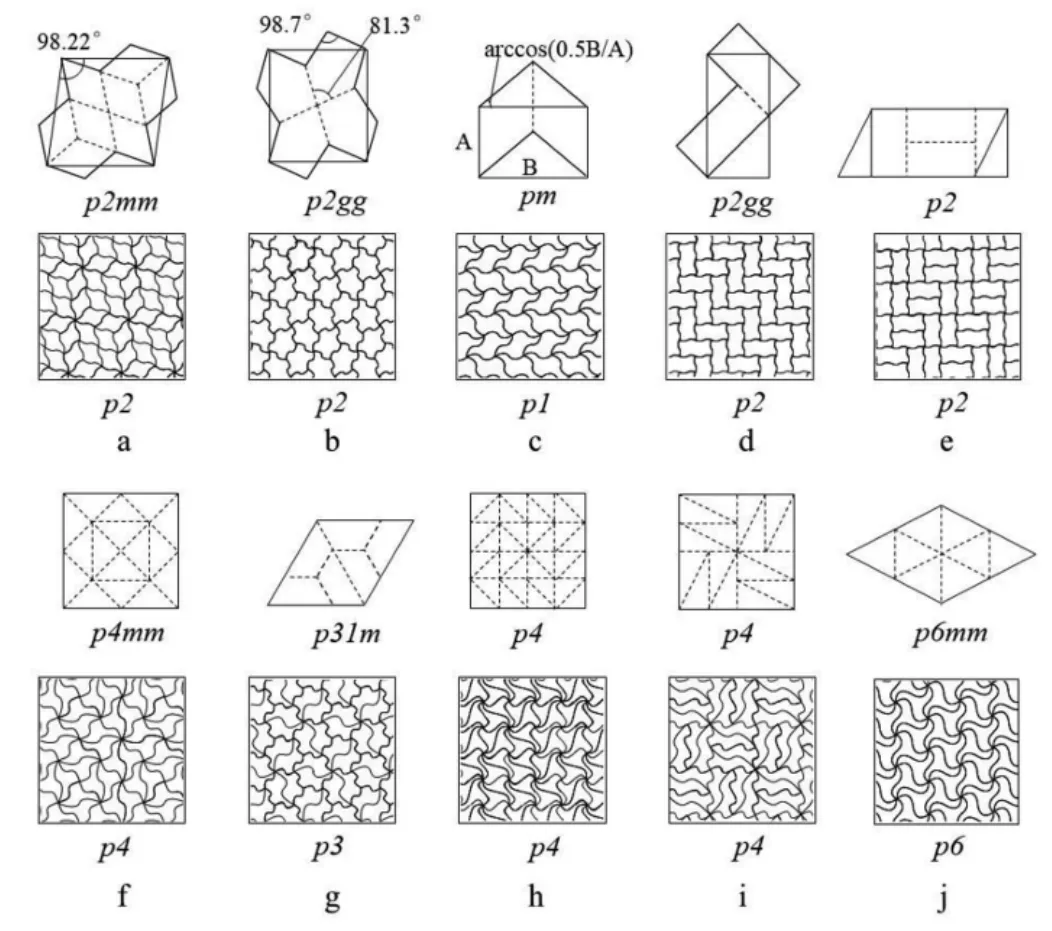
图11 EGLPZ 未按照“过轴心N 分割”规则分割成N’个等边多边形（GX）及其TNX 拼合铺排图，a-e；P 任意分割成多个半等边多边形（GX/2）及其TNX/2 的拼合铺排图, f-j

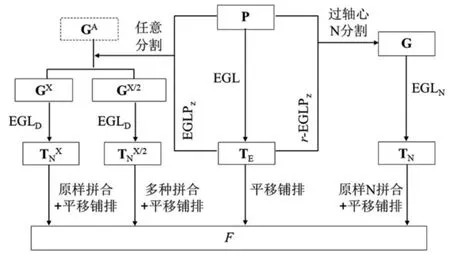
图12 不同曲边单面单砖的形成及其相互关系

6 结论

根据平面点阵理论，可严密铺排成无穷大平面F的点阵型平面单砖（包括异形、曲边等复杂平面）的最基本形状为平面群的元胞。本文提出的单形，单面，曲边平面砖T 分为基础平面砖TE和三种多重平面砖TN、TNX和TNX/2。其中TE可顺两个方向平移铺排成F；多重平面砖需要多重拼合成为TE。T 建立的一般过程是以一个凸角多边形作为基形，然后在保持基形面积不变的条件下按一定规律将所有直线曲线化。TE的基形P 包括不同对称性的5种元胞和3 种凸角平行六边形。P 的曲线化必须通过平行边偶（LC）用任意线同替换，使P 的凹凸面互补的等盈亏（EGL）操作来实现。由此得出结论：所有EGLP 均为TE，所有TE必须是EGLP，不同的TE可以通过EGL 操作相互转化。

P 或者具有旋转轴的折线型r-EGLPz按照“过轴心N 分割”的规则可得到N 个（N=2，3，4，6）相同的凸角x边型（x=3，4，5，6），其可作为TN的基形G。G 存在0~3对LC 和0~4 条独立边（IL）。其中LC 包括平行LC（0°夹角）和2π/6、2π/4、2π/3 夹角LC。G 的曲线化也需要进行相应的等盈亏（EGLN）操作：LC 用任意线同替换，IL 用二重线替换。

实际上，P 和很多EGLPz也能够不按照“过轴心N分割”规则分割成N'个相同的多边形，除了等边多边形（GX和GX/2）之外，一般不能全接触，不能进行EGLN操作，故不能全曲线化，只能以非全接触多边形GA的形式拼合铺排为F。

等边x 边形GX可以在保持原来角度的条件下用x条相同的二重线全替换（EGLD操作）实现曲边化，形成TNX。P 和很多EGLPz也能够以任意的方式分割出多个由特殊的多边形GX/2拼成的半等边多边形。GX/2含有2-3 条等长边和1 条独立的分割边。其也能进行类似上述的EGLD操作（等长边由相同二重线替换，独立边由单独二重线替换），由此形成的TNX/2可以拼合成多种不同对称性的图案。

图12 总结了各种T 之间的逻辑关系。本文的核心依据是平面点阵理论以及由此推断的不同分割方法和等盈亏操作方法。从此人们可以理解、判断并预测所有异形多边形及其曲边化产物的平面特性；可以设计出不同对称性，不同风格的多边形及全曲边平面砖。