赵春然，尹新国，朱孟正

(淮北师范大学 物理与电子信息学院，安徽 淮北 235000)

在经典和量子物理中，大量的基本现象都是源于束缚在势阱中的运动，其典型特征呈现为周期性运动，例如钟摆的往复运动、琴弦的振动、行星的轨道运动以及微观原子中的电子运动等，人们把这种物体在平衡位置附近往返运动叫做振动或机械振动；只要势能曲线有极小值，就会有振动.物理学中的振动，不仅仅指的是直观上感觉到的位置做周期性的往复运动，而是泛指物理量做周期性变化的运动形式[1].例如在RC电路中的电流和电压都做周期性变化，这种被称为电磁振动；振动并不限制在机械运动范围.

1 简谐振动基本概念

利用质点和刚体运动规律研究这种特殊的而又具有普遍意义的运动形式——振动，是切实可行的.然而，简谐振动是最简单、最基本的振动；研究简谐振动是分析、理解更复杂振动现象的基础.质点在线性回复力作用下围绕平衡位置的运动，叫做简谐振动.在理想的物理系统中无耗散力作用下，若质点相对于平衡位置的位移为x，则质点所受的回复力为

F=-kx.

(1)

在这里结合具体例子谈简谐运动的动力学特征，以弹簧振子为例[2-3]，水平的弹簧自由伸展时质点的位置是平衡位置(忽略弹簧的质量)，以该位置为原点建立坐标系Ox，坐标x表示振子，也就是质点偏离平衡位置的位移.并且x也表示弹簧的伸长(压缩)量，当x的绝对值很小时，由库克定律可知弹性力F与x之间成线性关系.若振子的质量为m，根据牛顿第二定律可得

(2)

位移x对时间t的二阶微分，用在x上面加两个点表示，即加速度.上式也可以表示为

(3)

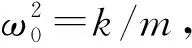
(4)

位移x对时间t的一阶微分，用在x上面加一个点表示，即速度.显然，运动方程(3)式为二阶的常系数齐次微分方程，它的解可以表示为位置坐标x关于时间t的正弦或余弦函数：

x=Acos(ω0t+φ)，

(5)

其中A、φ为该二阶微分方程的通解中两个待定的积分常数，可以根据简谐振子的初始条件确定，设初始时刻t=0时振子的位置坐标、速度分别为x0、v0，则振幅、初相位角分别为

(6)

(7)

三角函数正切值在0～2π范围间有两个角度与之对应，因此初相位角具体数值确定应须代回式(5)中或是从式(5)计算出的速度根据方向以判定取舍[1].

2 例析微振动问题

例一个质量均匀分布的半球体置于水平桌面上，平衡时半球上的平面朝上并与桌面平行，该半球体的半径为R，质量为m，若在半球体的圆平面边缘处微小幅度按下随即松开，则半球体在桌面上做小范围运动，假设运动中半球相对做桌面无滑滚动，证明该半球是做简谐振动.

解析1半球在水平桌面上做小幅度往复无滑滚动，质量均匀分布的半球作为刚体，做刚体的平面运动.为了清晰的表达运动中的半球所具有的动能，假想把半球补足成一个完整的球体，如图1所示，完整球体的动能分为随质心的平动动能和绕质心的转动动能：

图1 置于水平桌面的匀质半球体Fig.1 Homogeneous hemisphere placed on a horizontal table

(8)

(9)

其中：vc是完整球体的质心平动速度；Ic是完整实心球体绕过球心O并垂直于纸面水平轴的转动惯量，可表示为

(10)

因为是无滑滚动，所以vc=ωR；对于完整实心匀质球体的质心和其球心是重合的.当刚体的质心速度以及绕质心转动角速度一定的情况下，平动动能是与刚体的质量成正比，转动动能与该刚体绕固定轴转动惯量成正比的[4-6]，所以半球体的平动动能为

(11)

截取半个球体的截面若是与当前的转动轴垂直，则半球体相对于该轴的转动惯量[7]为式(10)的一半.然而，如图1所示，并不是垂直于当前的转动轴，根据反映转动惯量性质的两个定理中的一个——垂直轴定理，质量均匀分布的半球体绕通过球心O并垂直于纸面的水平轴的转动惯量为

(12)

故此，半球体绕通过球心O并垂直于纸面的水平轴的转动动能为

(13)

根据质心的计算公式，可以求得质量均匀分布的半球体的质心[8]到球心的距离为

(14)

因在桌面上发生了小范围移动，造成了半球体的对称轴，也就是半球质心所在的虚线，与竖直轴间形成了一个夹角θ，见图1.假定半球上的平面朝上并与桌面平行时(如图1中浅色线条所示)，半球体的重力势能为零，则当前时刻半球体的重力势能为

Ep=mglO′C′(1-cosθ).

(15)

因相对桌面做无滑滚动，摩擦力不做功，故系统的机械能守恒，即有

(16)

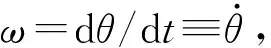
(17)

从(17)式可以看出半球体在水平桌面上的小幅度往复运动，确实是做简谐振动，其振动的固有周期为

(18)

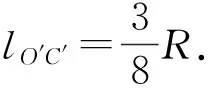
图2 从半球体的质心出发分析其微振动Fig.2 Analyze the micro-vibration from the center of the hemisphere mass

(19)

(20)

(21)

因此可算出半球体的动能为

(22)

半球上的平面朝上并与桌面平行时，半球体的质心C′位置最低，假定此时体系重力势能为零，则当前时刻半球体的重力势能为

Ep=mglO′C′(1-cosθ)，

(23)

因系统做无滑纯滚动，耗散力不做功，故可以采用机械能守恒，即有

(24)

因E不随时间改变，对上式关于时间做微分处理，变化量就是角度θ，可得

(25)

考虑到系统是在做微振动，即θ很小，则sinθ≈θ、cosθ≈1，所以得

(26)

(27)

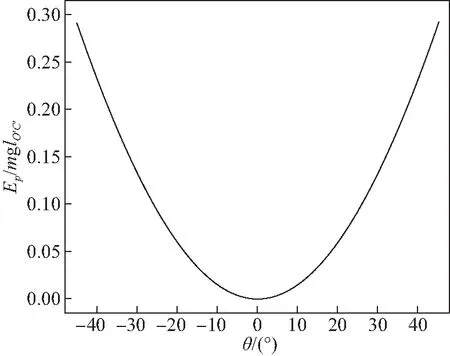
图3 半球体在水平桌面做无滑滚动时势能随角度的变化Fig.3 The change of potential energy with angle when a hemisphere rolls on the horizontal table without sliding

(28)

其周期为

(29)

延伸比较：假设这里的半球体不是置于水平桌面，而是绕通过球心并与纸面垂直的水平轴线做无摩擦的摆动，这个轴线是固定的.根据定轴转动的角动量定理：

(30)

若做小幅度摆动，则

(31)

其中

(32)

做简谐振动的固有周期为

(33)

从上面的两种解析结果可以看出：虽然两种分析都得到了半球体的微振动是简谐振动，但是振动的频率、周期不一样，说明有一个解析肯定是有问题的，问题出现在解析1里面.解析1中有一处明显的错误：在于对转动惯量的理论知识的掌握不够深入，知道垂直轴定理，但对运用垂直轴定理的先决条件是什么不清楚；垂直轴定理只适用于刚体的厚度为无穷小的薄板.因而，在解析2中，直接根据转动惯量的定义，计算出半球体以过球心沿切面轴线转动的转动惯量.第二处错误比较隐蔽或者说是迷惑性比较大，那就是在计算半球体总的机械能时，采用了所谓的“补偿法”补全半球体，解析中体系的动能分解成平动动能和转动动能，均是以完整球体的质心(球心)来计算出球体的平动动能和转动动能，对平动动能减半处理、对转动动能根据半球体绕过圆心轴的转动惯量多少而定，然而在计算体系势能的时候又采用半球体的质心来考虑，得出的结果也反映出体系微振动会引起系统势能起伏，所以说迷惑性比较大.实际上，问题的重点就在于计算动能采用完整球体的球心作为质心，然后动能适当减半处理，而计算体系势能时，采用半球体质心.计算动能和势能的标准不统一，造成动能对真实结果的偏差.比如说，采用“补偿法”，以球心作为质心，完整的球体在运动过程中势能不会变化，就不会有势能极小值，因此不会具有形成往复运动的条件，这样解释就比较好理解解析1中用“补偿法”的不妥之处.

3 结论

首先对简谐振动基本理论进行了梳理，再通过举例详细分析了系统偏离平衡位置的微振动，并剖析了错误解答的症结所在，使我们更加深刻的理解刚体做平面运动的动能计算和微振动问题处理的要点.在求解中运用了反映转动惯量性质的两个定理：平行轴定理、垂直轴定理，在熟知这两个定理后计算一些特定的刚体针对某个轴的转动惯量将会比较简单，但也要注意垂直轴定理的适用范围.