王永庆， 赵诗琪， 申宇瑶， 马志峰

(北京理工大学 信息与电子学院，北京 100081)

信噪比是一种有效的通信质量评价指标.作为先验信息，它可以作为信道分配、功率控制、指导编解码和解调算法选择的重要依据[1]. 经典的信噪比估计算法可分为两类：数据辅助(data aided，DA)[2]和非数据辅助(non data aided ，NDA)[3]. NDA估计器由于不需要同步、应用场景广而被广泛研究，包括基于同相/正交(inphase/quadrature，I/Q)和基于包络(envelope based，EVB)的估计器. I/Q估计器[4]基于载波同步，估计性能在宽信噪比范围内接近克拉美罗下限(Cramér-Rao lower bound，CRLB). 然而，相较于 I/Q估计器，EVB信噪比估计器不需要严格的恢复载波，信噪比可以作为先验信息辅助载波同步环路，对于多电平星座信号更加适用. 因此，本文主要研究EVB估计器.

矩量法(method of moment，MoM)是一种常用的EVB估计方法，它利用信号与噪声之间的不相关性来计算信号和噪声的功率. M2M4估计器[5]具有简单的优点，然而，对于非恒模星座，随着信噪比的增加，其估计性能会显著下降. 因此，文献[6]中使用了建立在矩商线性组合基础上的高阶统计量(最高为8阶统计量)进行信噪比估计，性能得到了改善，特别是针对2级和3级星座. 然而，它对高信噪比条件下的正交幅度调制(quadrature amplitude modulation，QAM)信号的估计性能急剧下降. 基于经验分布函数(cumulative distribution functions，CDF)的方法是另一种EVB估计器，使用Kolmogorov-Smirnov(KS)算法[7]，该算法在宽的信噪比范围内对各种多级星座估计都是有效的. KS估计器的实质是在一系列确定的信噪比下比较接收信号(通常选择包络)的EDF与CDF. 与接收信号EDF最近的CDF相对应的信噪比就作为接收信号的估计值. 为了获得最佳匹配的CDF，需要遍历整个本地存储的信噪比区间. 因此，KS估计器的计算量大，在大规模待匹配信噪比区间的实际应用中受到限制. KS-BS估计器[8]通过二分法极大加快了匹配过程，虽然匹配复杂度较低，但在中、高信噪比时估计性能下降. WANG等[9]将匹配维数减少为1，但仍有许多加法运算.

为了在保证估计性能的前提下降低EDF估计器匹配复杂度，本文提出了一种改进的EDF估计器，通过线性多项式的重复迭代来加速匹配过程. 然后分析了该估计器的迭代过程和收敛速度，并通过仿真进行了验证.

1 EDF信噪比估计器概述

1.1 系统模型

在准静态频率衰落信道上的数字通信系统中，位同步后的符号速率采样点可以表示为

(1)

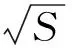
1.2 基本原理

对于EDF信噪比估计器，首先需要计算接收信号包络|rm|的经验分布函数(EDF)

(2)

式中：U(·)为阶跃函数，如果输入为非负，则等于1，否则等于0；{zn}为本地储存信噪比下信号包络理论累计分布函数(CDF)的Nref个离散采样点.

(3)

式中Q1(a,b)为一阶Marcum-Q函数.

将接收信号的EDF与本地储存所有信噪比下的CDF作比较，得到每一信噪比下EDF与CDF的最大距离(Φk)为

(4)

遍历ρk，选择具有最小最大距离相对应的信噪比作为接收信号的信噪比估计结果.

2 改进的EDF信噪比估计器

基于经验分布函数的信噪比估计器需要遍历本地存储所有的信噪比来获得最小最大距离. 在相同的信噪比估计范围内，估计精度Δρ决定了所需匹配的信噪比数目K. 较高的信噪比估计精度会带来较多的匹配次数和加法运算，因此，实际应用中需要在估计精度和匹配计算的复杂性两者中进行折中考虑. 基于这个问题，本文提出了一种改进的EDF估计器，不需要遍历本地所有存储的信噪比，采用“以直代曲”的思想，通过线性多项式的重复迭代来加速匹配过程，可以降低EDF估计器的匹配复杂度，并且具有比较高的估计性能.

如果接收信号信噪比的估计值与真值接近，则EDF曲线与CDF曲线就很接近，两者的最大距离就很小. 相反，如果估计的信噪比偏离真实值，则最大距离会很大. 最大距离曲线(Φ-曲线)随本地存储所有信噪比的变化呈“对勾”形状，如图1所示.Φ-曲线的零点对应于最小-最大距离. 因此，找到Φ-曲线零点的过程就相当于EDF与本地存储所有信噪比下CDF曲线的匹配过程，快速找到Φ-曲线的零点就可以代替大量的匹配过程，从而不需要遍历整个信噪比区间. 整个匹配过程就可以转换为在参考定义域为本地存储所有信噪比的情况下，求解式(4)的根.

图1 16-APSK/QAM的Φ-曲线Fig.1 Φ-curve of 16-APSK/QAM

KS -BS估计器实质是利用二分法求解式(4)的根，二分法操作简单，且必然是收敛的，是一种可靠的算法. 但在二分法中，每迭代一次，搜索区间缩小1/2，也就是说，解的不定范围每次只能缩小1/2. 因此二分法是一种是收敛速度非常缓慢的算法，估计精度受限于迭代次数，估计精度越高所需的迭代次数就越多. 本文使用“以直代曲”的思想，用2个迭代点构建一个线性多项式来反复代替Φ-曲线，用2个迭代点的斜率近似代替Φ-曲线的切线斜率，并用线性多项式与横轴交点的横坐标作为Φ-曲线的根的近似. 通过连续迭代，用线性多项式的根不断逼近Φ-曲线的零点，找到近似解，并将其作为估计结果.

2.1 迭代过程

假设k1=1,k2=K是第一次迭代区间的初始值，利用Φk1,Φk2构造线性多项式 ：

(5)

式(5)可以作为Φ-曲线的直线替代，并令其为0，得到其与横轴交点的横坐标，如式(6)所示为

(6)

式中k3为式(5)的零点，并将k3作为第一次迭代过程中Φ-曲线零点的近似解. 在第二次迭代中，用函数值Φk3替换max{Φk1,Φk2}，作为下一次迭代的初始值之一. 同时，k3被相应地替换为k1或k2，再次根据式(5)构建线性多项式，求解下一次迭代过程Φ-曲线零点的近似解. 当搜索区间小于1，搜索结束，并将搜索区间端点对应的信噪比的均值作为对接收信号的信噪比估计，否则不断重复上述步骤.

由于上文提出的迭代过程本质上是一种线性化方法，因此当曲线近似为直线时，就可以保证迭代策略的收敛性. 如果搜索区间两个迭代端点分别位于Φ-曲线零点两侧，则可以将其中一个迭代点的函数值取反，使零点一侧的曲线对称于x轴，将曲线转换为近似直线，以保证迭代过程的收敛性，并加速收敛过程. 可以根据以下两种情况判断是否需要将其中一个迭代点的函数值取反:①由于有限定义的本地存储信噪比区间，根据式(6)所求的根k3可能在定义域[1,K]之外，如图2(a)所示，这种情况就需要将其中一个迭代点的函数值取反，将Φ-曲线零点一侧的曲线翻折，将Φ-曲线转化为近似直线;②函数值Φk3大于迭代区间端点最大函数值max{Φk1,Φk2}，如图2(c)所示，也需要将其中一个迭代点的函数值取反.

综合上述分析，本文将式(6)改写为

(7)

图2给出了本文改进EDF估计器寻找最佳匹配CDF曲线的整个迭代过程. 如图2(a)所示，第一次迭代以[1,K]为首次搜索区间，作直线得到Φ-曲线零点的近似替代值k3. 由于k3∉[1,K]，根据式(7)将函数值Φk3取反. 重新以经过(k1,-Φk1),(k2,Φk2)的直线代替Φ-曲线，得到近似解k3，Φk1<Φk2，因此k3替代k2作为第二次迭代过程的端点值. 如图2(b)所示，再次“以直代曲”，得到第二次迭代过程的近似解k3，由于Φk1>Φk2，用k3替代k1，作为第三次迭代过程的端点值. 如图2(c)所示，

图2 迭代过程Fig.2 Iterative process

在第三次迭代中，由于Φk3>max{Φk1,Φk2}，根据式(7)将Φk2取反，进而求得k3. 经过三次迭代，k3已经非常靠近原始Φ-曲线的零点，所对应的信噪比ρk3可以作为接收信号信噪比的最佳估计值.

2.2 收敛速度

收敛速度是指迭代序列逼近局部最优值的速度，是评价迭代算法性能的重要指标. 收敛阶p用来衡量序列的收敛速度：

(8)

本文改进的EDF估计器收敛阶p≈1.618[10]，具有超线性收敛速度，这意味着本次迭代的信噪比估计误差与上一次迭代误差的1.618次方成正比. 当k1迅速逼近接近k2时，两个迭代端点k1、k2所在直线的斜率将接近其中一个迭代点的导数Φ′(k). 零点k3的计算实质上可如式(9)表示. 在这种情况下，p=2[11]. 也就是说，迭代过程在根附近近似平方收敛.

(9)

3 仿真结果

本节首先通过蒙特卡罗模拟的方法对各信噪比估计器对接收信号的性能进行了仿真验证，针对每个仿真点，均进行了104次蒙特卡罗仿真[13]. APSK、QAM信号是常用的多电平星座，因此针对16-APSK信号(常用的两电平星座)和16-QAM信号(常用的三电平星座)进行了仿真. 本地存储信噪比的CDF是在理论连续CDF曲线上采样的1 000个离散点，即Nref=1 000.

3.1 估计性能

图3 不同观测长度下的归一化均方误差Fig.3 Normalized mean square error under different observation lengths

上面的仿真验证了当观测符号长度M>700时，矩估计器和EDF估计器的估计性能都趋于稳定，因此选择观测符号长度M=700作为对不同信噪比下偏差(Bias)和归一化均方误差(NMSE)的仿真参数. 本节仿真将本地存储的信噪比设置为Ω={0,0.5，1.0，…,24.5，25.0}(dB)，对偏差和归一化均方误差进行性能评估. 仿真结果如图4所示. 此处提供的CRLB来自参考文献[14].

图4 估计性能Fig.4 Estimated performance

图4(a)和4(b)显示了各信噪比估计器对16-APSK的结果. M2M4在中、高信噪比下存在明显的偏差，但M8几乎是无偏估计. 在低、中等信噪比下，由于噪声较大，且处于整个搜索区间的边缘，用直线代替Φ-曲线存在较大的偏差，本文改进的信噪比估计器估计偏差和NMSE略高于KS估计器. 在10～18 dB，搜索区间处于整个搜索区间的中部，用直线代替Φ-曲线较精确，本文改进的信噪比估计器估计性能优于原KS算法估计器，但同样在高信噪比区间边缘20～25 dB出现性能损失. 然而，在测试的所有信噪比下，本文改进的信噪比估计器优于KS-BS估计器. 图4(c)和4(d)显示了各信噪比估计器对16-QAM的结果. M2M4和M8在中、高信噪比下都有较高的偏差和NMSE，估计性能恶化. 本文改进的信噪比估计器性能介于原KS估计器和KS-BS估计器之间，劣于原KS算法估计器，优于KS-BS算法估计器. 本文改进的信噪比估计器和KS-BS估计器的性能损失都是由于搜索造成的. 然而，与KS-BS估计器相比，本文改进的信噪比估计器具有更高的精度.

3.2 收敛速度

表1 基于EDF的信噪比估计器所占资源比较

4 结 论

基于经验分布函数的信噪比估计器在实际应用中需要在估计精度和匹配计算的复杂性两者中进行折中考虑.基于此问题，在保证信噪比估计精度的前提下，本文使用“以直代曲”的思想，用线性多项式的根不断迭代逼近最大距离曲线的零点，找到最佳匹配的CDF曲线.本文改进的EDF估计器避免了遍历所有的信噪比去找EDF曲线与CDF曲线的最小最大距离，仅需要几次匹配迭代就可以找到最佳匹配的CDF曲线.仿真结果表明，与矩估计器相比，本文改进的EDF估计器在宽信噪比范围内对多电平星座信号的信噪比估计都是有效的；与KS算法EDF估计器相比，本文改进的EDF估计器极大减少匹配次数和加法运算的次数，但是估计性能在信噪比区间边缘有轻微的性能损失；与KS-BS算法EDF估计器相比，本文改进的EDF估计器有更快的收敛速度，进一步减小了EDF和CDF的匹配次数，在中、高信噪比具有更小的估计偏差和归一化均方误差.对于需要高估计精度的系统，所提改进的EDF估计器收敛速度快，比KS估计器和KS-BS估计器更具实用性.