陈 喜，唐有绮，柳 爽

（上海应用技术大学机械工程学院，上海201418）

引言

随着科学技术的迅速发展，轴向运动功能梯度结构的磁力控制在航空航天、机械工程和交通运输等领域得到广泛的应用。工程实际中，机械设备可能处于高温差的环境中或系统受到外部机械力作用而产生较大的振动，从而降低设备的可靠性和安全性，甚至带来重大的经济损失。因此，研究磁场作用下轴向运动功能梯度结构的振动特性具有理论意义和实际意义。

轴向运动结构的研究最早可以追溯到Aiken［1］的实验观测和分析。许多优秀的综述反映了该领域不同时期的研究进展［2-8］。王乐等［9］求解自由边界下轴力对Timoshenko梁的横向振动影响。Tang等［10］研究了不同边界条件下轴向运动Timoshenko梁的固有频率、模态以及临界速度。杨晓东等［11］研究了两端铰支边界条件下Timoshenko模型轴向运动梁的横向振动问题。刘星光等［12］对三种典型轴向运动结构的振动特性进行了对比。Ghayesh等［13］研究了轴向运动Timoshenko梁参数振动中的周期响应问题。Chen等［14］研究了黏弹性轴向运动Timoshenko梁在参数共振下的动态响应问题。Ghayesh等15］研究了轴向运动Timoshenko梁的非线性受迫振动及其稳定性。周远等［16］研究了黏弹性阻尼作用下轴向运动Timoshenko梁的振动特性。唐有绮［17］研究了轴向运动黏弹性Timoshenko梁的稳态响应。An等18］通过广义积分变换方法，研究了轴向运动Timoshenko梁的动态响应。文献［19-20］研究了以轴向速度为周期性改变参数的轴向运动Timoshenko梁参数振动问题。Hu等［21］建立了磁场环境下轴向运动的导电材料梁的力学模型，推导了磁弹性振动方程。张立保等［22］研究了磁场中轴向运动导电梁的自由振动。文献［23-24］对超导和铁磁材料等构件在电磁场作用下的弯曲、失稳等问题进行了深入的研究。王杰等［25］研究了磁场中轴向运动导电梁的主共振问题。胡宇达等［26］研究了在平行导线间轴向运动铁磁梁的主共振问题。Liu等［27］研究了磁场中轴向运动导电梁非线性自由振动的位移响应。崔雪［28］推导了梁双向振动固有频率和阻尼比的表达式。Su等［29］通过发展动态刚度法，研究了功能梯度Timoshenko梁的自由振动。Zhong等［30］研究了悬臂功能梯度梁在不同载荷作用下的问题。Alshorbagy等［31］基于幂律理论，研究了材料沿轴向或横向分层的功能梯度梁的动力特性。Lai等［32］导出了功能梯度梁大振幅振动的精确解析解。Thai等［33］发展了功能梯度梁弯曲和自由振动的各种高阶剪切变形梁理论。刘金建等［34］研究了幂律指数和剪切变形对功能梯度梁弯曲和自由振动响应的影响，分析了轴向运动功能梯度黏弹性梁横向振动的稳定性问题。赵凤群等［35］由Hamilton原理建立轴向运动功能梯度Timoshenko梁运动微分方程组。邓昊等［36］求解了沿轴向指数分布的功能梯度Timoshenko梁的状态空间传递矩阵方程。随岁寒等［37］研究了轴向匀速运动功能梯度梁的稳定性，变速运动时的参数振动及其稳定性。

然而文献［9-20］只研究了轴向运动Timoshenko梁的振动特性，文献［34-35］也只研究了轴向运动功能梯度梁的振动特性，都未考虑磁场作用的影响；文献［21-28］只研究了磁场作用下轴向运动Timoshenko梁的振动特性，未涉及功能梯度材料的性质对振动特性的影响；文献［29-33，36］只研究了静态功能梯度梁的振动特性，未考虑陀螺项的影响。目前针对轴向运动结构的振动特性还存在一些问题，比如衰减系数和固有频率的对应性问题。本文研究了磁场中轴向运动功能梯度Timoshenko梁的振动特性，给出了其对应的控制方程组和简支边界条件。取适当参数，使用复模态法得到了速度和频率的对应关系，得到了前四阶固有频率和衰减系数，并通过微分求积法进行了验证。

1 控制方程

如图1所示，长l、高h、宽b的矩形梁，所受单位面积轴向拉力为P。功能梯度导磁梁置于磁场强度为B（0，By，0）的横向恒定磁场中，并以速度c沿x轴方向运动。

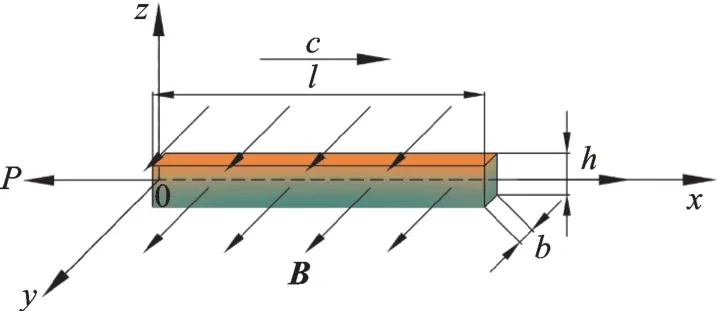
图1 磁场作用下轴向运动功能梯度梁的物理模型Fig.1 The physical model of axially moving functionally graded beam under magnetic field

两种材料的弹性模量E（z）、密度ρ（z）、电导率λ（z）、剪切模量G（z）均沿厚度方向按各组分体积以幂函数形式梯度变化

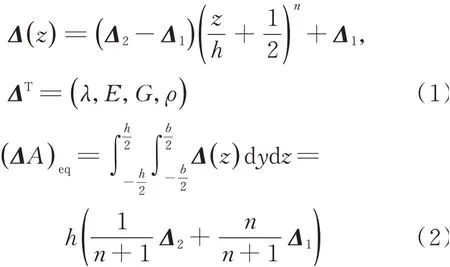
式中z为横截面上任意点距几何中面的距离，n为功能梯度指数，A=h×b为截面积。

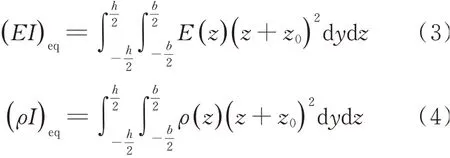
假设坐标原点建立在功能梯度材料梁的中性面上，功能梯度材料梁中金属材料组分的体积比例系数Vn为梁厚度方向坐标z1的幂函数

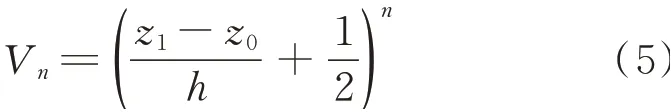
式中n为梯度指数，z0为梁中性面真实位置与文献［37］假设距梁上表面1/2处的中性面之间的距离。根据Timoshenko梁修正理论，假设φ为梁截面弯曲转角，可知功能梯度材料梁的正应力表达式为

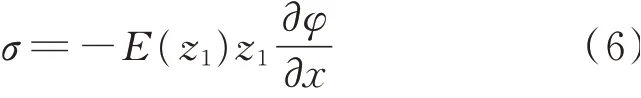
功能梯度梁弯曲时横截面正应力应满足以下表达式

轴向运动功能梯度梁受电磁场作用产生的感应电流密度

式中w（x，t）为梁运动时产生的横向振动位移，V为速度矢量，i，j和k分别为沿坐标轴x，y和z方向的单位向量。

感应电流密度产生的洛伦兹力为

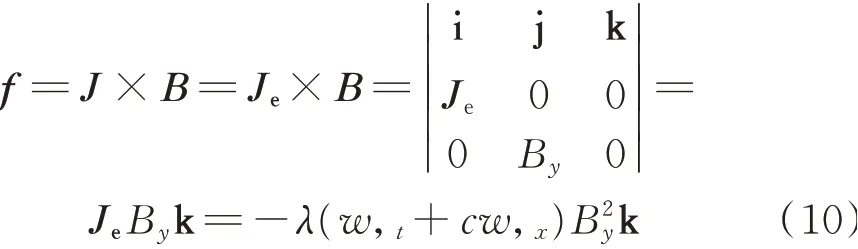
动能为

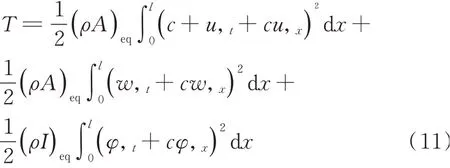
势能为

电磁虚功W1的变化可写为

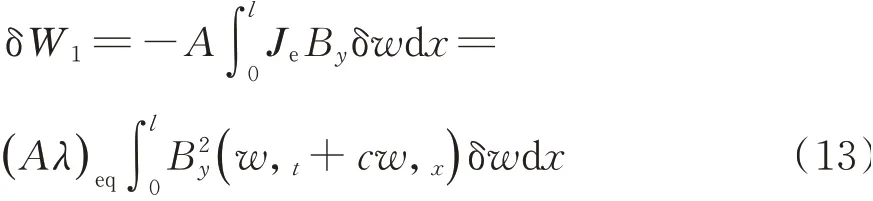
变形功W2的变化可写为

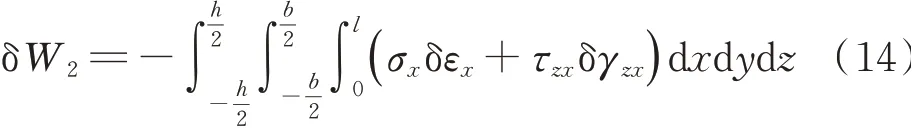
应力和应变分别为

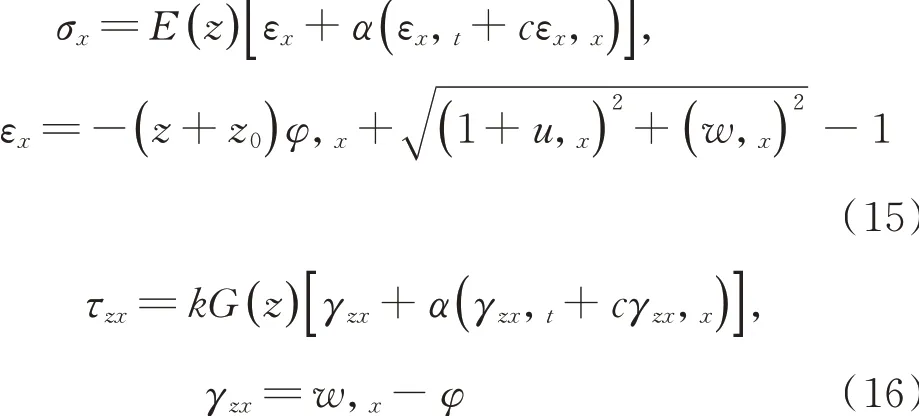
式中σx（x，t）和εx（x，t）分别为正应力和正应变，τzx（x，t）和γzx（x，t）分别为剪应力和剪应变，k为Timoshenko梁的截面形状因子，α为Timoshenko梁的黏弹性系数。

基于Hamilton原理

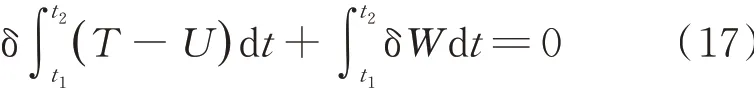
可以得到其无量纲形式的控制方程组和相应的简支边界条件：

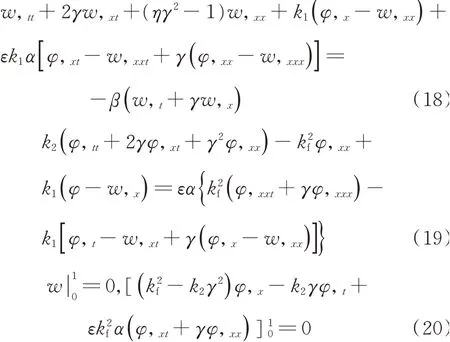
式中η=1/［1+ks/（2EA/l）］为支撑刚度参数；ks为支撑刚度。支撑刚度参数的变化范围为0-1。当支撑为完全刚性支撑时（ks→+∞），η=0；当支撑为完全柔性支撑时（ks=0），η=1。其他无量纲参数为

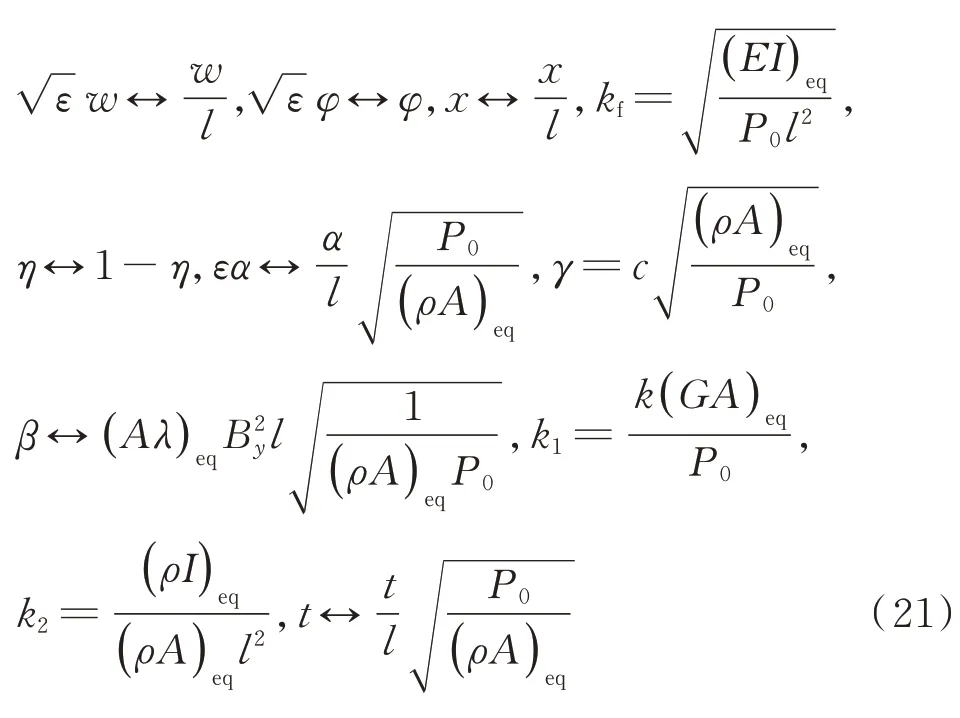
2 复模态方法

假定式（18）和（19）具有分离变量的形式：

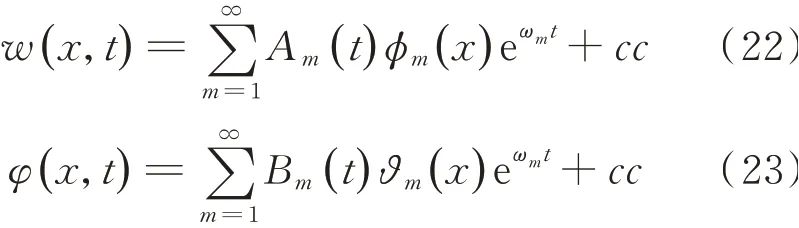
式中cc表示前面各项的复共轭。四阶齐次线性复系数常微分方程组的解可以写为

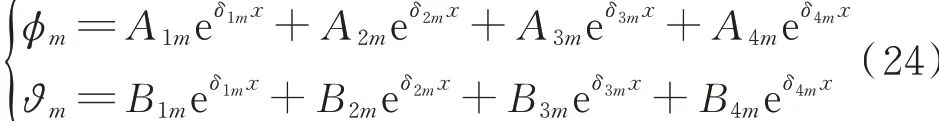
将式（22），（23）和（24）代入式（18）导出

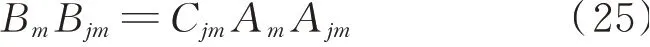
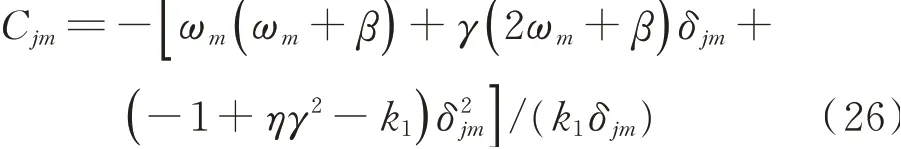
其中解耦式（18）和（19），并将式（22），（23）和（24）代入解耦后的式子得到

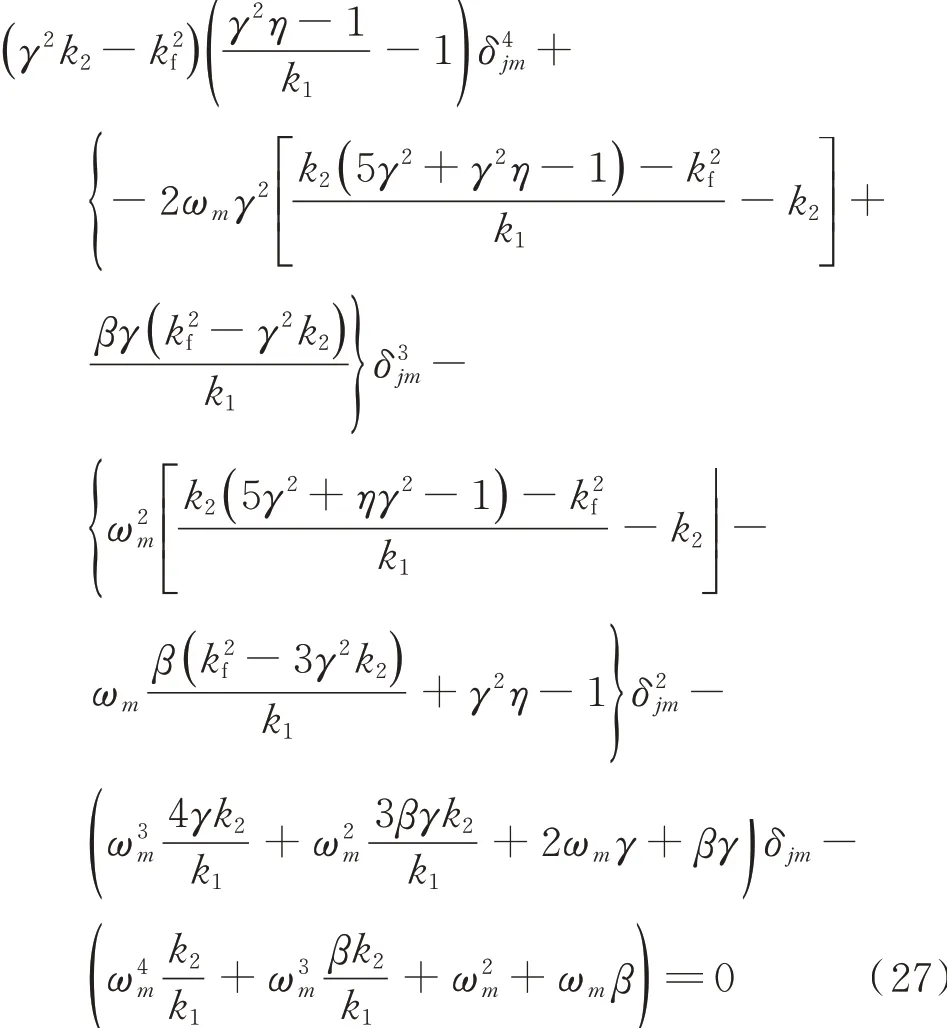
整理得到频率方程

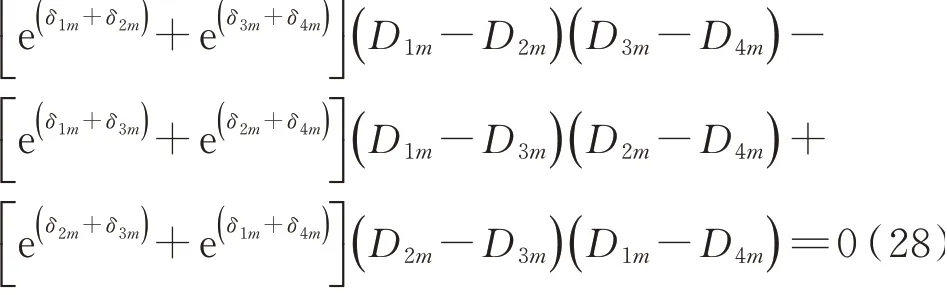
从而导出模态函数

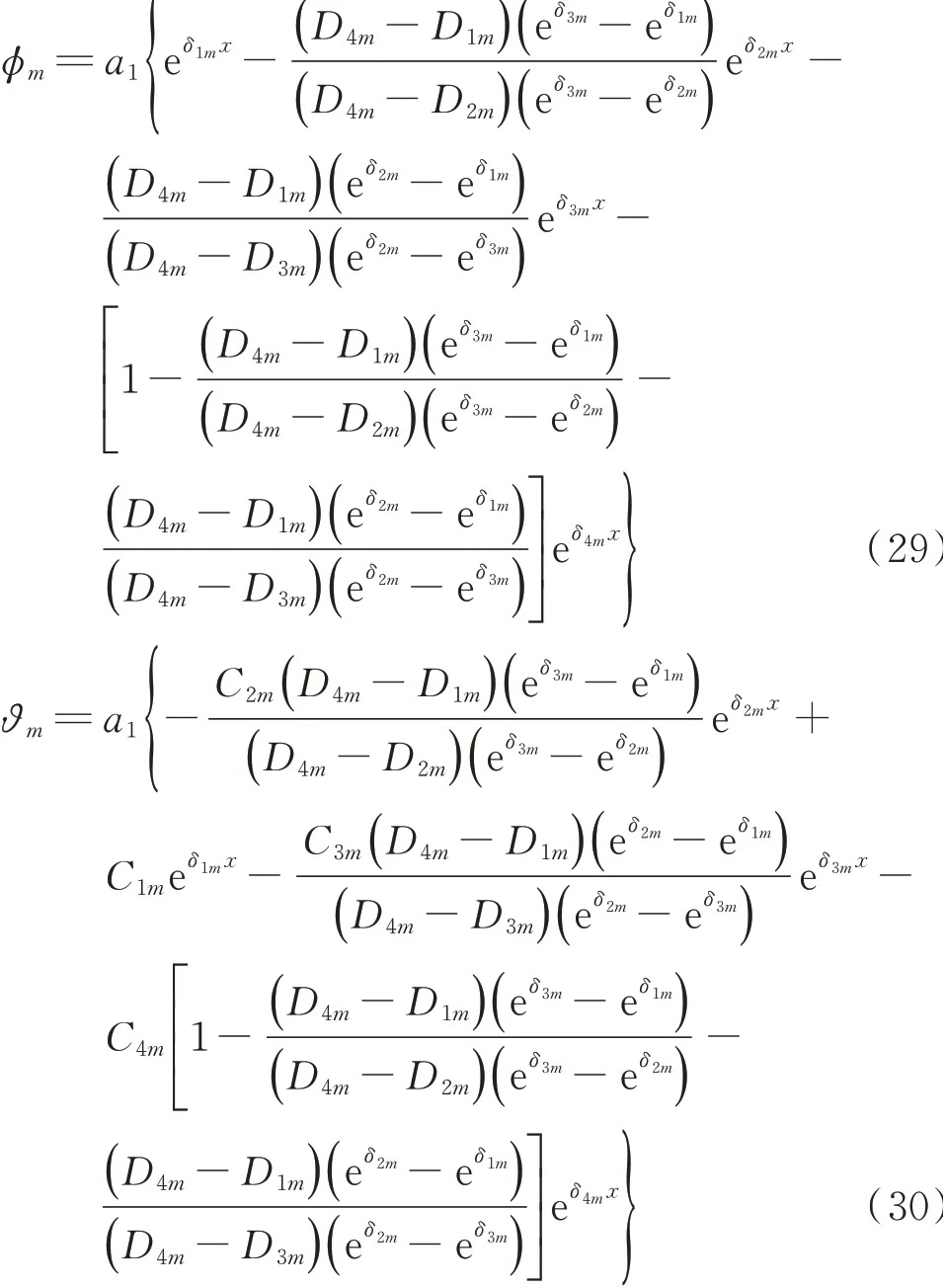
其中

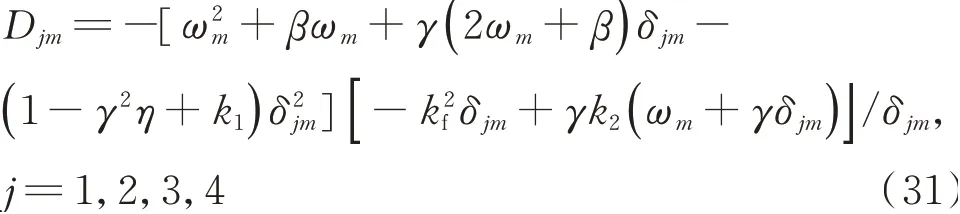
给定陶瓷和金属材料的物性参数如表1所示，若给 定n=1，λ=1.17×106，η=0.5，k1=76.1836，k2=

表1 陶瓷和金属材料的物性参数Tab.1 Physical properties of ceramic and metal materials

4.4×10-3，kf=0.8781和γ=2，对于不同的磁场强度By，前两阶固有频率随轴向速度的变化如图2所示。当By=2.5，n=1时，在不同支撑刚度参数下前两阶固有频率随轴向速度的变化如图3所示。当By=2.5，η=0.5时，在不同功能梯度指数下前两阶固有频率随轴向速度的变化如图4所示。

从图2-4中可以明显看出，固有频率随着轴速的增加而连续减小。当固定轴向运动速度时，从图2（a）中可以看出，较大的磁场强度对应较小的固有频率；从图2（b）中可以看出，磁场强度对于二阶固有频率的影响较小。因此，磁场强度的引入，使一阶系统的临界速度有了明显的减小。从图3中可以看出，当固定轴向运动速度时，较大的支撑刚度参数对应较大的固有频率。因此，支撑刚度参数的引入，使系统的临界速度有了显著的增加。当固定轴速时，从图4中可以看出，较大的功能梯度指数对应较小的固有频率。功能梯度梁的固有频率在两种材料非功能梯度梁的固有频率之间随n的变化而变化。

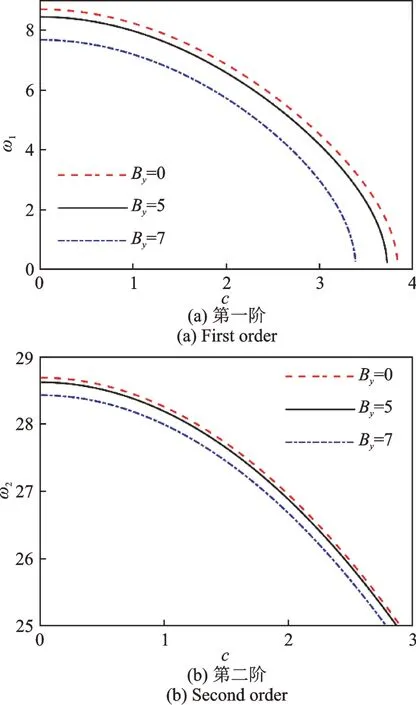
图2 不同磁场强度下前两阶固有频率随轴向速度的变化Fig.2 The variation of the first two natural frequencies with axial velocity under different magnetic field intensities

图3 不同支撑刚度参数下前两阶固有频率随轴向速度的变化Fig.3 The variation of the first two natural frequencies with axial velocity under different support stiffness parameters

图4 不同功能梯度指数下前两阶固有频率随轴向速度的变化Fig.4 The variation of the first two natural frequencies with axial velocity under different functional gradient indices

3 数值验证

本节引入微分求积法［38-40］对以上近似解析解进行数值验证。Timoshenko梁的计算区域为x∈［0，1］。x方向的网点数为N。通过微分求积法将控制方程（18）-（20）离散为：

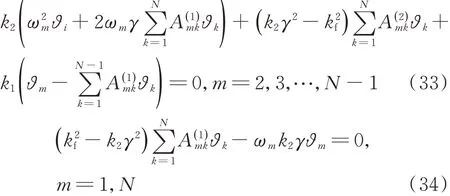
应用修正权系数法修正后写为矩阵形式

式中M，G和K分别为质量矩阵、陀螺矩阵和刚度矩阵。它们的维数均为2N×2N。S表征广义矩阵，其维数为2N×1。

给定N=15，n=1，By=2.5，λ=1.17×106，η=0.5，k1=76.1836，k2=4.4×10-3，kf=0.8781和γ=2，图5给出了线性派生系统前四阶的衰减系数和固有频率随着轴向速度的变化情况的两种处理结果的比较。δ1，δ2，δ3，δ4分别表示前四阶的衰减系数；ω1，ω2，ω3，ω4分别表示前四阶相应的固有频率。从中可以看出，衰减系数呈现不对称性。图6为图5中点a，b，c位置放大图。图中连续的线表示解析出的前四阶衰减率以及固有频率，不连续的点则表示数值分析的结果。对比结果表明，解析的结果与数值分析的结果在数值上是十分相近的。当不考虑磁场时，一阶与二阶、一阶与三阶、二阶与四阶固有频率分别在点a，b，c处产生耦合，三点处相关的固有频率完全相等（相应的衰减系数不同），不会出现分离。当考虑磁场时，三点处相关的固有频率依然存在耦合，但是数值已有差别，此时耦合固有频率具有分离特性。

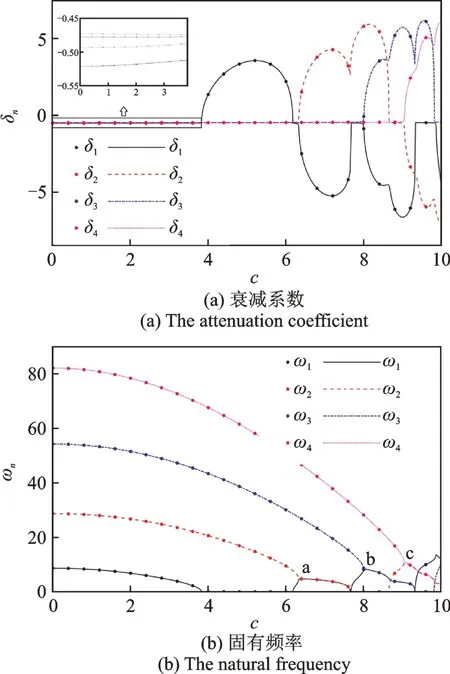
图5 前四阶衰减系数和固有频率随轴向速度的变化Fig.5 The attenuation coefficients and the natural frequencies of the first four orders vary with axial velocity

图6 点a，b，c放大图Fig.6 Partial magnifications of points a，b and c

4 结论

本文运用复模态法和微分求积法研究了磁场作用下轴向运动功能梯度Timoshenko梁的振动特性。通过一系列的数值算例，描述了磁场强度、功能梯度指数和支撑刚度参数变化对固有频率的影响。研究结果表明：随着轴向运动速度的增大，梁的固有频率减小的速度越来越快。随着磁场强度和功能梯度指数的增大，梁的固有频率减小；随着支撑刚度参数的增大，梁的固有频率增大，但其随轴向速度的增大而减小的速度越来越慢。磁场强度的变化对于第二阶固有频率影响并不明显。衰减系数呈现不对称性，耦合固有频率呈现分离性。