石 舢

（喀什大学，新疆喀什 844000）

1 引言

在大学阶段所学习的课程中，高等数学所覆盖的内容非常广泛，微积分在数学领域中作为其重要的分支，在力学、天文、物理等科学的发展上都做出了巨大的贡献.通常，我们所熟悉的是一元方程的微积分.但是要想拥有更多的数学知识，仅仅掌握一元方程的微积分显然是不够的，我们还需要掌握二元方程微积分的相关知识，这无论是对今后的日常学习、研究生考试还是工作来说都有很大帮助.在二元方程的微积分中，曲面方程的积分不仅是数学课程的重点，同样也是难点.对曲面积分的计算，我们经常将其与以前所学过的积分的计算思路、方法与技巧联系起来，解题过程看起来复杂难懂.弄清了曲面积分计算的方法，我们不仅可以更好地掌握曲面积分的性质，对曲面积分有更深入的了解，而且还能够提高对曲面积分的计算能力，更加熟练地掌握关于曲面积分计算的一些技巧，这对今后学习其他更加复杂的方程微积分的求有很大的帮助.

通常，我们在实际学习过程中会发现大部分曲面积分题目都很难做到迎刃而解，尤其在计算第二型曲面积分的时候.比如在解第二型曲面积分时易混淆正负号，对高斯公式的运用不是很灵活，不知道巧妙地利用对称性解答等问题.本文通过介绍各种曲面积分例题，对曲面积分的计算技巧进行归纳总结.

2 曲面积分的计算

2.1 第一型曲面积分的计算

第一型曲面积分的解题步骤（二重积分法）：

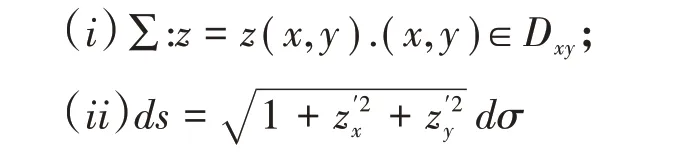
第一型曲面积分实则是转化为二重积分进行计算，要求学生要熟练掌握二重积分的相关知识；不一定非要将曲面∑向xoy面作投影，将z看成x,y的函数，也可以将曲面∑向xoz面作投影，将y看成x,z的函数或是将曲面∑向yoz面作投影，将x看成y,z的函数.到底向哪个面作投影，要根据具体的题目做决定，使计算更加方便.

下面将列举几个例题，以便熟悉第一型曲面积分的解题技巧.

2.1.1 替代法

解析：被积函数与曲面方程左半部分并不是成一个倍数关系，如果被积函数比较复杂，但是可以利用曲面方程进行化简，也可进行替换.可以联想在曲线积分计算的时候.发现它们都有这个特点，即积分曲面的方程是可以代入到积分表达式中的.因为在曲面积分中，被积函数f(x,y,z)是在积分曲面Σ上取值的，x,y,z满足曲面Σ的方程（此性质在第二型曲面积分计算中同样也是适用的，后面不再加以说明）.切勿将此方法用在二重积分计算上，二重积分中的D仅代表积分区域，不少同学在学会曲线积分和曲面积分的时候再回去做二重积分时都存在这样的误区，下面给出一个简单例子让学生能够学会区分.

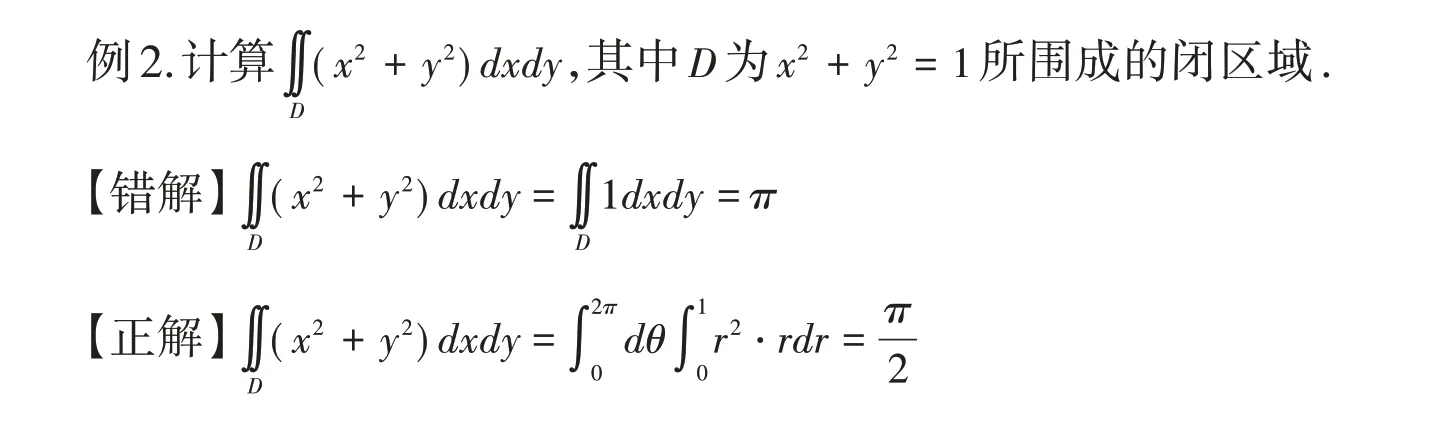
2.1.2 二重积分法

二重积分法是计算第一型曲面积分的最基本的方法，它是严格按照第一型曲面积分计算的步骤来进行的，是学生必须要掌握的方法.

2.1.3 利用被积函数的奇偶性及曲面的对称性［1］

【解】法一：曲面∑在xoy平面上的投影区域为D:x2+y2≤1，

因为积分曲面关于yoz平面对称，而x3y关于x为奇函数，故

分析：通过观察发现，被积函数前半部分是关于x的奇函数，后半部分是关于x的偶函数，而曲面∑关于yoz平面前后对称.此类题目就可以利用曲面积分的对称性，将题目进行化简，减少计算量.方法二与方法一相比，方法二更充分地运用了第一型曲面积分的普通对称性和轮换对称性［2］，这就需要学生对第一型曲面积分的性质掌握清楚.

2.2 第二型曲面积分的计算

第二型曲面积分又叫作对坐标的曲面积分.很多学生在学到曲面积分的时候，发现第二型曲面积分要比第一型曲面积分更加难懂，是令人感到头疼的一个知识点.下面给出了一些关于第二型曲面积分的解题技巧，学生若能够熟练地掌握第二型曲面积分的计算方法，多做题目，学会更多的解题技巧和方法，定能攻克这个难点.

设∑：z=z(x,y)，其中(x,y)∈Dxy，则，若∑上一点的法向量与z轴夹角为锐角，那么二重积分前带“+”号，若∑上一点的法向量与z轴夹角为钝角，那么二重积分前带“−”号［3］.

综上所述，可以看出第二型曲面积分的计算显然与第一型曲面积分的计算有很大差别，我们首先要判断二重积分前面“±”号，可以用七个字总结：“一定，二代，三计算”.针对第二型曲面积分的计算应该怎么解，下面列举若干例题进行讲解.

2.2.1 通过投影法化为二重积分

2.2.2 利用高斯公式求解

注：通过例题5，我们发现若采用直接计算法，则运算十分复杂且容易出错，高斯公式最大的好处就是能减少计算量.但是使用高斯公式求解的时候，有以下两点需要注意：首先要保证P(x,y,z),Q(x,y,z),R(x,y,z)在Ω 具有一阶连续偏导数，否则不能直接使用高斯公式；其次，如果曲面它不是封闭的，这个时候可以通过添加辅助曲面∑1的方法将积分曲面补成封闭曲面，最后减去被积函数在曲面∑1上的积分即可.

【解】补曲面∑1:Ζ=2，方向朝上，则

分析：本题引用的是《高等数学下册》课本231 页例3，这里与书本解法有所不同.通过观察，发现=0，那么能不能用高斯公式求解呢？此处曲面∑并不是封闭的，故添加辅助平面使其封闭，再利用高斯公式，这样一来简便很多，如果按照教材上面的解法则较为复杂.

3 结语

本文主要介绍了曲面积分的相关知识，它包括第一型和第二型曲面积分两种类型.对于前者，首先通过观察被积函数和曲面方程，看能否采用替代法.如果不能，再考虑其他方法，比如投影法，最后换成二重积分进行计算.后者与前者相比较为复杂，在计算的时候，通常情况下，首先考虑能否利用高斯公式，这样在很大程度上能够减少计算量，但关键的一点是要判断P,Q,R是否具有一阶连续偏导数；其次如果曲面不封闭，则可通过添加辅助曲面的方法将积分曲面补成封闭曲面.总之，是要将原来复杂的第二型曲面积分化为一个三重积分进行计算，而新得到的三重积分比原曲面积分简单.