阮晓露, 吴晓霞,2,3*

（1.闽南师范大学数学与统计学院,福建漳州363000；2.数字福建气象大数据研究所,福建漳州363000；3.数据科学与统计重点实验室,福建漳州363000）

设G=(V(G),E(G))是n阶简单图,记P(G,x)= det(xI-A(G))为G的特征多项式,A(G)为其邻接矩阵.A(G)的特征值为G的特征值.因为A(G)是实对称矩阵,所以A(G)的特征值都为实数,不妨设λ1(G)≥λ2(G)≥…≥λn(G).树是连通无圈图,记T是一个树图，Pn代表n个顶点的路，若V′⊆V(G),E′={uv∈E(G)|u,v∈V′},则称G′=(V′,E′)是G中由V′生成的导出子图.

1982 年,Cvetković[1]提出确定λ2(G)≤1 的图类,对于这个问题,经过研究者们多年的努力,当前关于特征值确定的图类已有许多研究结果,但仍未彻底解决,1993 年Cao[2]刻画了λ2(G)<的简单图,Cheng[3]刻画了λ2(G)≤1 且仅有三个特征值的简单图.由于确定出λ2(G)≤1的所有图较难,研究者们开始利用第二大特征值刻画特殊的图类,1982 年Neumaier[4]给出了树图第二大特征值的重要性质,1998 年Shu[5]刻画了λ2(T)≤1的树图,2012年Stanić[6]刻画出λ2(T)≤的树图,2021年Liu[7]刻画出不包含K1,3,K5-e作为导出子图且λ2(G)≤1 的图.利用Neumaier[4]提出的关于树图第二大特征值的性质,给出了λ2(G)≤的树图的充要条件.

1 预备知识

引理1[4]1)设u是－图G的任意顶点,C(u)是在图G中包含顶点u的所有圈集,则

2)设uv是图G的任意边,C(uv)是在图G中包含边uv的所有圈集,则

引理2[8]设G=(V(G),E(G))是n阶图,V′⊆V(G)且|V′|=k,则

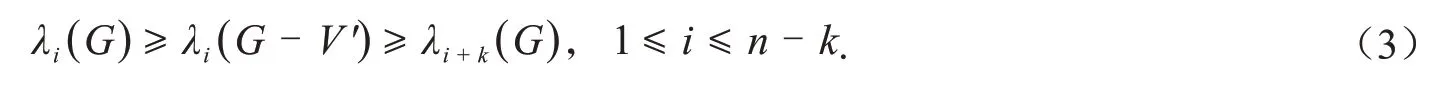
引理3[9]设G是n阶简单图,则λ1(G)≥λ1(Pn)当且仅当G≅Pn时等号成立.

引理4[4]设G≅G1∪G2∪…∪Gω()G,则

引理5[4]设T是n阶树且λ2(T)≤λ,则

1)要么存在点u∈V(T),使得λ1(T-u)≤λ；

2)要么存在边uv∈E(T),使得T-uv=T1∪T2,有λ1(T1-u)<λ<λ1(T)且λ1(T2-v)<λ<λ1(T).

2 主要结论

定理1记T是树,则λ1(T)≤ 3 当且仅当T同构于K1,3或Pi,i= 1,2,…,5 是其中之一,特别地λ1(P5)=λ1(K1,3)=.

证明充分性计算K1,3或Pi,i= 1,2,…,5的第一大特征值可得结论成立；

必要性 设树T,|V(T)|=n且λ1(T)≤,假设n> 5,由引理3可知

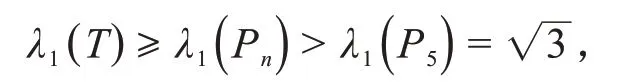
这与λ1(T)≤矛盾,故n≤5,计算得

如图1,从而T只能同构于K1,3或Pi,i= 1,2,…,5是其中之一,证毕.

图1 点变换图Fig.1 Vertex transformation graph

在下面叙述和证明中,将涉及一类图,图1的T′和图2的T″,在T′中,si(i= 1,…,12)是任意正整数且至少有一个不为零,代表着K1,3和Pi,i= 1,2,…,5用其任意的顶点(除去同构的情况)连接点u的数目,例如当s2=2,s10= 3,si= 0,i≠2,10 时,T′≅Tˉ；同理在T″中,ki(li),i= 1,…,6 是任意正整数且至少有一个不为零,代表着Pi,i= 1,2,…,4 用其任意的顶点(除去同构的情况)接点u(v)的数目.

图2 边变换图Fig.2 Edge transformation graph

定理2记T是树,令u为树T中的一个点,则λ1(T-u)≤当且仅当T≅T′(如图1),其中Si(i=1,…,12)是正整数且至少有一个不为零.

证明充分性因为T≅T′,所以

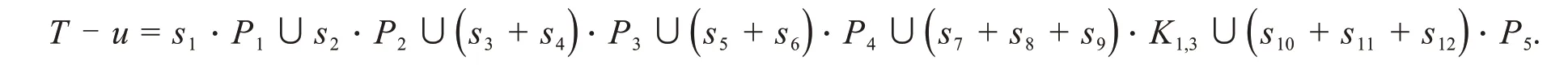
从而由引理4,定理2可知

必要性 若d(u)= 1,则u是T的悬挂点,因为λ1(T-u)≤由定理1 可知T-u同构于P1,P2,P3,P4,P5,K1,3其中之一,从而T≅T′,其中仅存在一个si≠0.若d(u)=k≥2,则u是T的割点,从而T-u=T1∪T2∪…∪Tk,k≥2,不妨设λ1(T1)≥λ1(T2)≥…≥λ1(Tk),因为≥λ1(T-u)=λ1(T1),由定理2可知Ti同构于P1,P2,P3,P4,P5,K1,3(i= 1,2…,k)其中之一,从而T≅T′.其中至少存在si,sj,i≠j不为零,证毕.

定理3记T是树,令uv为树T中的一条边,使得T-uv=T1∪T2,则λ1(T1-u)<<λ1(T)且λ1(T2-v)<λ1(T)当且仅当T≅T″(如图2),ki,li,i= 1,…,6至少有一个不为零.

证明充分性 如图2 所示,T≅T″,T-uv=T1∪T2,T1-u=k1⋅P1∪k2⋅P2∪(k3+k4)⋅P3∪(k5+k6)⋅P4,从而由引理4,定理2 可知同理λ1(T2-v)<.

必要性 因为T-uv=T1∪T2,所以d(u)≥2,u是T1的割点,从而妨设λ1(T11)≥λ1(T12)≥…≥λ1(T1k),因为由定理2,T i1(i= 1,…,k)只能同构于Pi,i= 1,…,4 其中之一,同理T2-u=T12∪T22∪…∪T l2,(l≥2),T i2(i= 1,…,l)也只能同构于Pi,i=1,…,4其中之一,从而T≅T″,证毕.

定理4若T≅T″.λ2(T″)≤ 3 当且仅当ki,li,i= 1,…,6满足表1中的取值.

证明令Pi(x)为Pi的特征多项式,根据引理1可得：

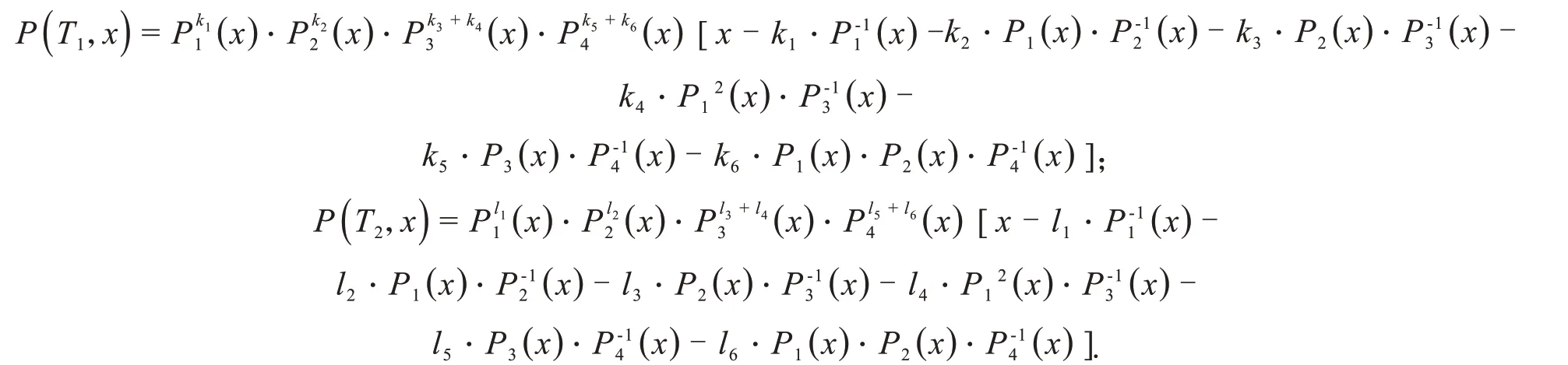
则

其中

取V′={u,v},|V′|= 2,则

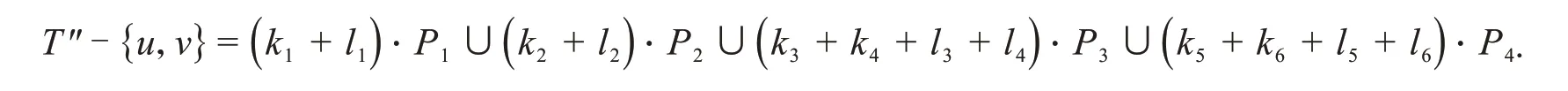
计算得

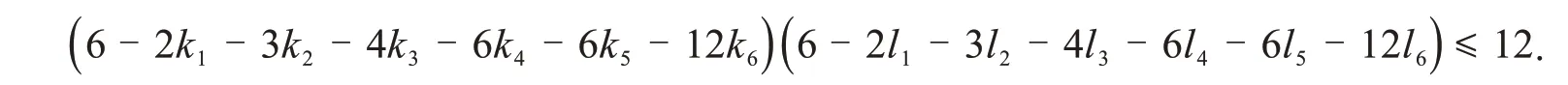
令a=(6 - 2k1- 3k2- 4k3- 6k4- 6k5- 12k6),b=(6 - 2l1- 3l2- 4l3- 6l4- 6l5- 12l6),因为λ1(T1-由引理2,可知同理即a< 0 且b< 0,由于ki,li,i= 1,…,6 是正整数,因为a=k且b=l与a=l且b=l,T″同构,所以a,b的取值满足以下情况：

1)a= -1且b= -1,…,或- 12；2)a= -2且b= -3,…,或- 6；3)a= -3且b= -4.

满足上述情况的ki,li,i= 1,…,6的取值见表1,证毕.

表1 ki(li)(i = 1,…,6)的取值Tab.1 The values of ki(li)(i = 1,…,6)

续表1

续表1

定理5设T是树,λ2(T)≤当且仅当

1)T要么是T′的任意导出子图；

2)T要么是T″的任意导出子图,其中ki,li,i= 1,…,6满足表1中的取值.

证明必要性 设树T,λ2(T)≤,由引理5 的1）与定理2 可知,T≅T′,由引理2 可知,T′的任意导出子图由引理5的2）与定理2可知T≅T″,其中ki,li,i= 1,…,6满足表1中的取值,同理由引理2可知,T″的任意导出子图

充分性 当T≅T′,由引理2 可知,从而T′的任意导出子图,第二大特征值也小于；当T≅T″,由定理4 可知,ki,li,i= 1,…,6 满足表1 中的取值时,有从而T″的任意导出子图,第二大特征值都小于证毕.