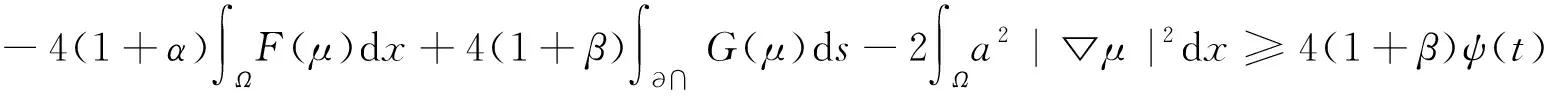具有罗宾边界条件的拟线性抛物方程解的整体存在和爆破现象
2021-12-07李志青
曾 鹏,李志青
(广州华商学院 数据科学学院,广东 广州 511300)
本文考虑下面的拟线性抛物方程
(b(u))t=▽·(a(u)▽u)-f(u),inΩ×(0,t*),

u(x, 0)=u0(x)≥0,inΩ
(1.1)
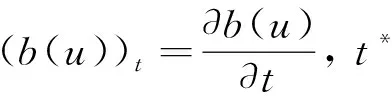
更多的关于拟线性方程或非线性方程的研究可参见文献[1-7].在许多情况下,这些技术被用于研究具有齐次Neumann边界条件的偏微分方程的爆破现象(见文献[8-11]).
(1.1)的一些特殊情形已经被解决了,Walter[12]研究了下面的问题:
(1.2)
给出了g的一些条件,得到了爆破解和全局解的存在性.Amann[13]考虑了以下问题:
(1.3)
得到了爆破解存在的充分条件.Zhang[14]讨论了如下问题:
(1.4)
文献[14]中不仅得到了全局解和爆破解的存在性,而且得到了全局解的上估计、 爆破时间的上界和爆破速率的上估计.丁和郭[15]考虑了以下问题:
(b(u))t=Δu+f(x,u, |▽u|2,t),
inΩ×(0,t*),
(1.5)
通过构造合适的辅助函数,利用极大值原理,成功地将[14]的结果推广到方程(1.5). 在文献[17]中, Payne、 Philippin和Vernier考虑了以下的初值问题:
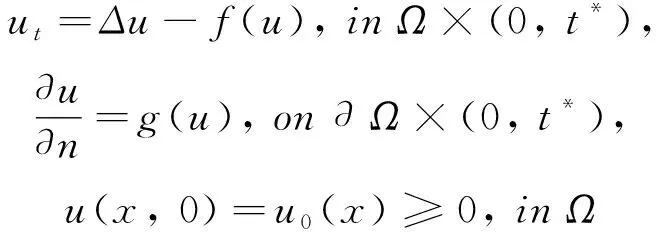
(1.6)
在对函数f和g作适当的假设的条件下,给出了全局解存在的充分条件,并在更严格的条件下,给出了爆破时间的上下界.
在本文中,我们主要将上面的结果推广到更一般的情况.由于g(u)是一个非线性项,问题可能更复杂,我们已经注意到一些作者已经开始关注具有非线性边界条件的系统(见[17-19]).
在本文中,我们在数据上找到足够的条件来保证u(x,t)始终存在.在对问题(1.1)的数据作一些适当的处理,只有在某有限时刻爆炸,该解才有可能不全局存在. 它们爆破还是不爆破主要取决于f的形式, 边界数据g,初始数据u0,函数a,b以及Ω的相关几何区域.当“爆破”出现时,我们推导出了爆破时间的下界. 注意到,不管解是否爆破,这个界仍然是有效的.本文还在比较严格的条件下得到了爆破时间的一个上界.
1 (1.1)式解的全局存在性
假设
(2.1)
其中m,n>1,k1,k2,k3>0.ξ>0
定义
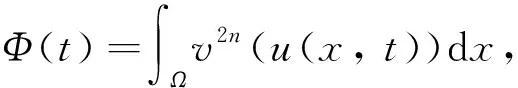
(2.2)
由(1.1)式和散度定理,我们有
(2.3)
根据a′<0以及(2.1)式、 (2.3)式,我们有
(2.4)
其中
(2.5)
此外再结合恒等式

有
(2.6)
其中ε1是一个大于0的任意常数.
在(2.6)式中,我们注意到
(2.7)
接下来,我们根据Payne和Shaefer在文[16]中推导出的Sobolev不等式
(2.8)
其中ε2是一个大于0的任意常数.
由(2.4)(2.6)和(2.8)式得
(2.9)
其中
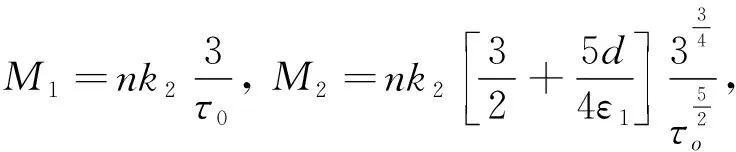

(2.10)
选取充分小的ε1和ε2使得M4≥0,利用Hölder不等式,则(2.9)式可变为
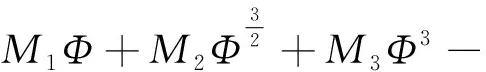
(2.11)
为了获得爆破时间的下界,我们考虑如下三种情况:
(1) 如果m=n+1, 则由(2.11)式得到
(2.12)
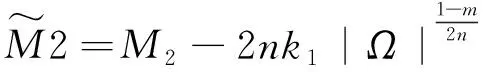
(2.13)
(2) 如果m (2.14) 其中ε3定义为 (2.15) 将(2.14)代入(2.11)有 (2.16) 其中 (2.17) 根据(2.6)式得到 (2.18) (3) 如果m>n+1, 则(1.1)式中非负整数解不可能爆破. 为了证明它,首先把(2.6)式代入(2.4)式得 (2.19) (2.20) 由此推出 (2.21) 如果μ在有限的时间内爆破,则(2.21)式应满足Φ′(t)≤0, 导致了矛盾. 我们用下面的定理来总结我们的结果. 定理1设μ(x,t)为R3中有界凸域Ω中问题(1.1)的解.假设数据a,b,f和g满足条件(2.1).如果在某个有限时刻t*内,μ(x,t)在度量Φ上是无界的,那么对于m=n+1,根据(2.13)式可得t*的下界; 对于m 在这一节中, 我们推导出了t*的一个上界.首先给出将在本节中使用的一些函数 (3.1) 在适当的条件下,我们能够得到下面的定理: 定理2如果μ是(1.1)的非负经典解, 且f,g,b和a满足 (3.2) 且 (abt)t≤0,bt>0. (3.3) 在(3.2)式中,α,β为正的常数且满足α≤β.此外, 设 (3.4) 则(1.1)的非负整数解在t*时刻爆破,t*的上界T定义为 (3.5) 证明计算 (3.6) 我们用到了式(1.1), (3.2)散度定理以及at<0,计算ψ(t)的导数,再一次使用式(1.1)和散度定理,有 (3.7) 从而得出ψ(t)是关于t的非减函数,再结合(3.4)式,有 ψ(t)≥ψ(0)≥0,t>0. (3.8) 由(3.6)和(3.7)推出 (3.9) 导致 (φ-(1+β)ψ)t≥0 (3.10) 对(3.10)从0到t积分得 (3.11) 其中 M=4φ-(1+β)(0)ψ(0) (3.12) 再结合(3.6)和(3.11), 有 φt(t)≥4(1+β)ψ(t)≥(1+β)Mφ1+β(t) (3.13) 再一次从0到t积分,通过(3.13)有 φ-β(t)≤φ-β(0)-β(1+β)Mt (3.14) 从而推出 t*≤T (3.15) (3.16) 因此,式(1.1)的解在有限的时间t*内是不存在的,并且从(3.15)中得到了爆破时间t*的上界,从而完成了定理2的证明.

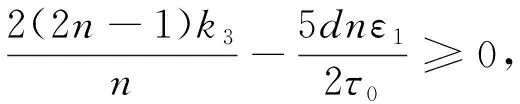
2 爆破时间的上界