唐 茜，涂细凯，郑笑雨，张冰冰

（1.湖北工业大学工业设计学院，湖北 武汉 430068；2.湖北工业大学机械工程学院，湖北 武汉 430068）

1 引言

过去二十几年来，多智能体的分布式协同控制一直是各学科非常感兴趣的话题，广泛的应用于分布式一致性、编队控制、包容控制和同步等。其中，一致性问题是分布式协同的关键问题[1-3]。一般来说，一致性问题的目标是设计合适控制算法，通过邻居智能体之间的局部信息交换，使得所有智能体的状态最终收敛到一致。

根据网络领导者的数量，一致性可以分为：无领导一致性、一致性追踪（Leader-Following）和多追踪（Multi-Tracking）等。近些年来，多追踪问题受到越来越多的注意。多追踪问题中，一个多智能体网络由多个群集组成，每个群集的所有跟随者的状态最终收敛于领导者的轨迹，同时，不同的群集之间收敛的轨迹不同[4-5]。注意到，代数图理论一直是研究多智能体一致性问题[6-8]的有效方法。

值得注意的是相比于位置信息，智能体的速度信息更难测量。因此，研究速度不可测的二阶多智能体系统的一致性问题是非常有必要的。前文提到大部分工作的前提是智能体之间信息的传输是连续的，然而，由于传输带宽的限制，这种传输形式不太可靠。因此，对于研究二阶多智能体系统的一致性问题来说，与连续数据相比，采样数据是更实际的来源。

在实际应用中，由于传输信息的带宽有限制，采样数据需要提前量化。因此，使用量化数据研究多智能体的一致性问题更有现实意义。进一步，量化误差对网络一致性性能的影响也不能忽视。但是，针对具有量化数据的二阶多智能体系统的一致性结论并不多。另一方面，在各种量化方法中，随机量化器的量化间隔是平均的，并且其量化误差的特性可以用于研究一致性问题。因此，针对二阶多智能体系统的一致性问题，采用了随机量化的方案进行研究。通信时滞的影响也应该要考虑，因其是降低网络性能的另一个因素。

针对考虑通信时滞的二阶多智能体系统，提出了一种量化的间歇控制规则用于解决系统的多追踪问题。不同于上述文献，仅仅使用了系统的采样位移信息，且控制输入是可变的。同时，引入了随机量化的方案，在传输之前量化位移信息。基于代数图论、随机量化和稳定性理论，分析得到了被控系统实现多追踪的一些充分必要条件。

符号定义：定义m阶单位矩阵为I∈ℝm×m，m阶零矩阵为0 ∈ℝm×m，并将I5∈ℝ5N×5N简化为I5。定义1ml∈ℝml×1为所有元素是1的ml阶列向量，Re(·)和Im(·)分别是复数的实部和虚部。AT和det(A)分别代表矩阵A的转置和行列式。⊗为Kronecker运算，P{·}和E{·}分别代表量化和期望运算。

2 预备知识和多追踪问题

2.1 预备知识

加权有向图G={V，ε，A} 中节点集为V={1，2，…m}，边集为ε⊆V×V，非对称加权邻接矩阵为A=[aij]∈ℝm×m。假如从节点j到节点i存在一个有向连接，则定义e(j，i)∈ε。当且仅当e(j，i)∈ε时aij＞0，假设没有自回路，也就是说对所有i∈V，令aii=0。定义节点i∈V的邻居节点集为Ni={j∈V，|(j，i)∈E}，节点i∈V的入度为。有向图G的对角矩阵为D=，拉普拉斯矩阵定义为L=D-A。

定义1：（子网络）定义网络Gs={Vs，εs，As} 为 网 络G={V，ε，A} 的子网络，满足Vs⊆V、Es⊆E和As⊆A。

2.2 问题描述

考虑具有m个节点的多智能体网络G={V，ε，A}，其由n≥2个子网络Gs={Vs，εs，As} (s=1，2，…，n)组成，每个子网络包含ms个节点，并且满足。同时，对任意s≠s′，Vs≠∅，满足。第sth个子网络的节点标记为Vs=，且令m0=0。

基于文献[9]中对随机量化的定义：假设数据h∈[-R，R]量化后长度为l比特，那么，我们可以得到量化点r=2l个和量化区间δ=2R/2l，以下为量化数据的方式：

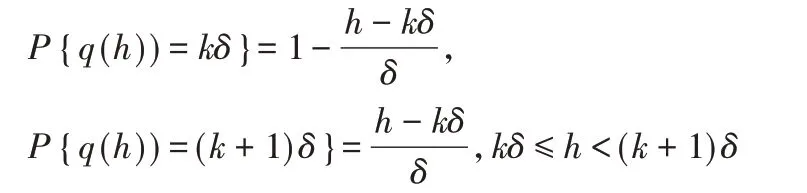
那么，对于此量化器我们可以得到一个很重要的特性：

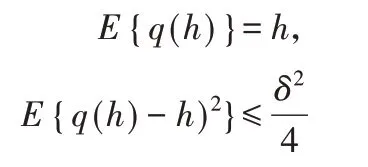
假设每个智能体具有如下二阶动态特性：

其中，xi(t)∈ℝ，νi(t)∈ℝ 分别是智能体i(i=1，2，…，m)的位移和速度量。μi(t)为状态反馈量。

第sth个子网络期望的追踪轨迹为：

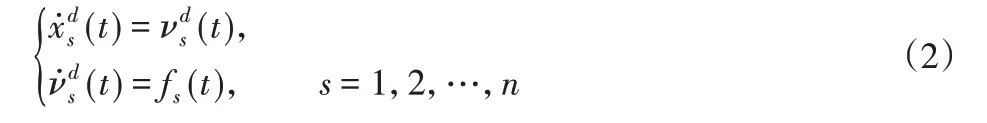
其中，fs≥0 ∈[0，+∞)在时间t内是分段连续的函数，(t)∈ℝ，∈ℝ表示第sth个子网络期望的位移和速度量。仅研究了二阶多智能体的匀速多追踪问题，即fs=0。

二阶多智能体系统（1）在期望轨迹为（2）下的多追踪问题可以重新写为：

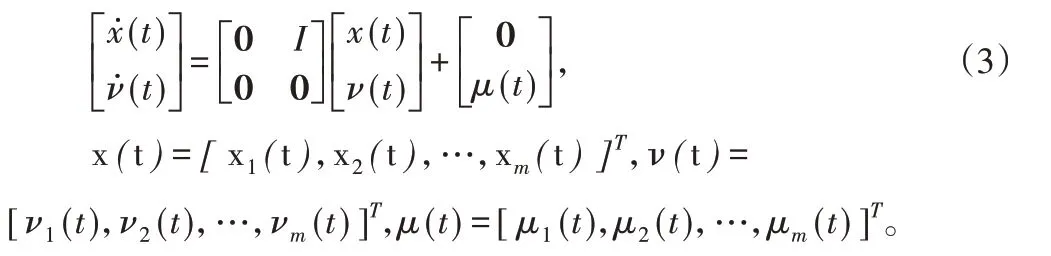
定义2：对任意初始状态，二阶多智能体系统（1）能够实现多追踪当且仅当

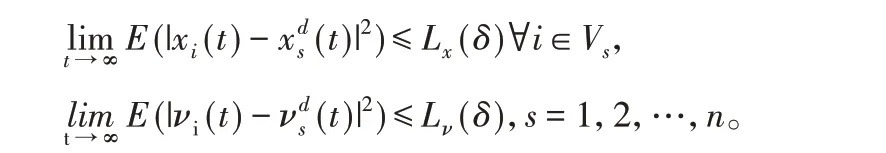
其中，Lx和Lν是关于δ的两个单调递增函数，且满足：

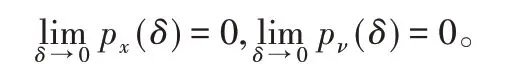
3 通信时滞下的量化间歇控制

在实际应用中，信息传输的过程中不可避免的存在时滞，这种情况对一致性控制协议的性能有很大的影响。假设多智能体系统通信时滞为τ，智能体之间只在采样时刻进行通信，采样时间序列为0 ≤t0＜t1＜…＜tk＜…，那么定义采样区间为ξ=tk-tk-1。针对多追踪问题提出了如下间歇控制方案：

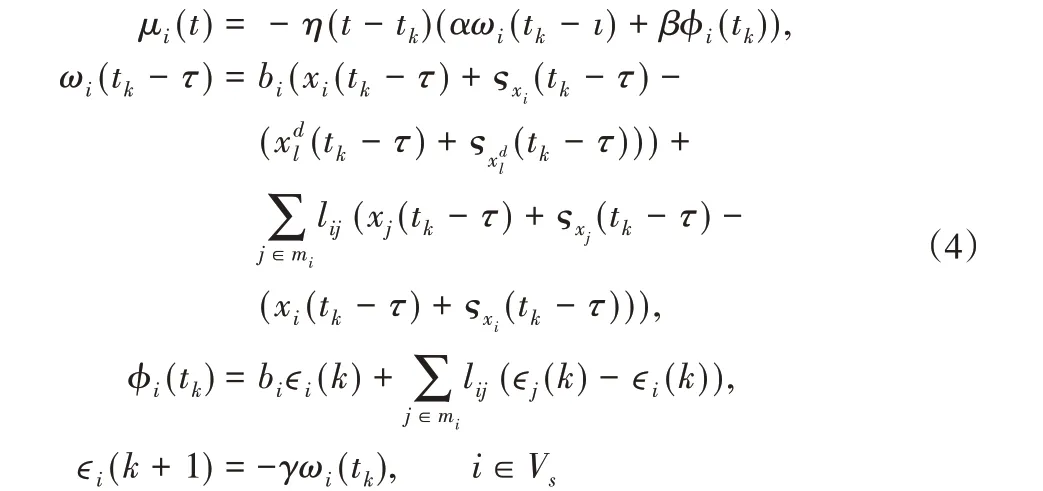
其中，控制参数α＞0，β＞0，γ＞0，tk＜t≤tk+1。ςxi(tk)=q(xi)-xi为第ith个智能体的位移量化误差为第sth个子网络的期望位移量化误差。η(t)为脉冲函数，表示如下：

其中，ε∈(0，ξ]为控制持续时间，函数(t)的选取可以依据不同的状态，可以为矩形函数、三角函数、梯形函数和非线性函数。从量化方程我们可以得到位移量化误差的如下性能：

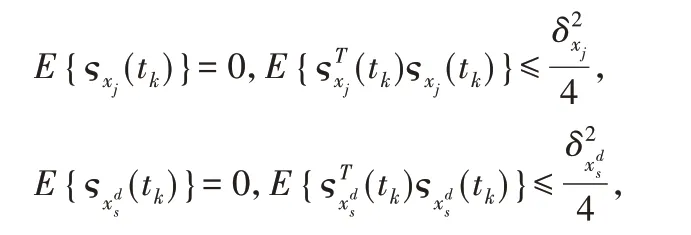
其中，δxj和δxds分别为智能体的位移和期望位移的量化误差区间。

令

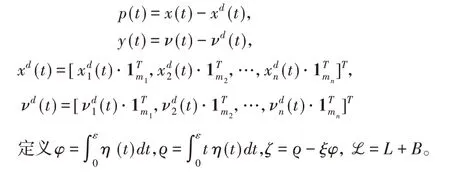
令H(tk)=[p(tk)T，y(tk)T，ϵ(k)]T，多智能体系统（1）可以改写为：

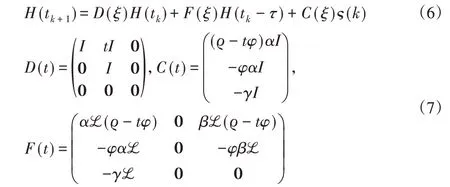
全文只考虑通信时滞满足τ＜ξ-ε的情况，

令：

引理1：[10]基于控制协议（4），二阶多智能体系统（1）可以实现多追踪当且仅当ρ(A)＜1，其中ρ(·)为矩阵A的谱半径。

证明：令

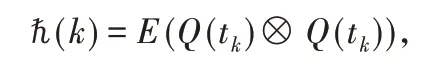
从式（8）可得，

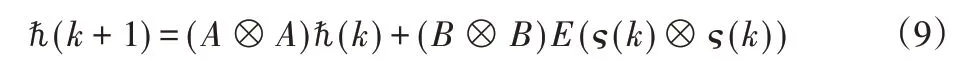
明显可知，

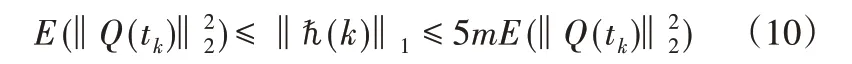
必要性：如果ρ(ℏ)≥1，那么ρ(ℏ ⊗ℏ)≥1，基于控制协议（4）的多智能体系统（1）一定是分散的，无法实现多追踪。

充分性：如果ρ(ℏ)＜1，那么ρ(ℏ ⊗ℏ)＜1，一定存在一个足够小的常数ı＜1满足‖ℏ ⊗ℏ‖2=ı＜1。那么

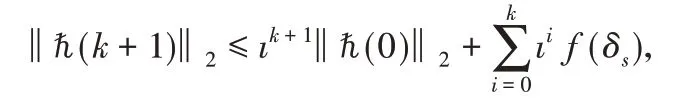
其中，f(δs)=。

由于ı＜1，可得：

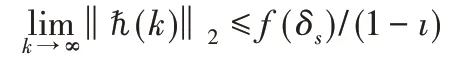
并且，

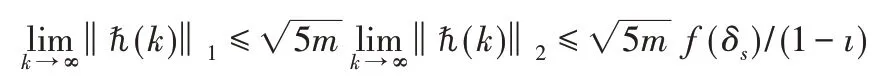
结合不等式（10），

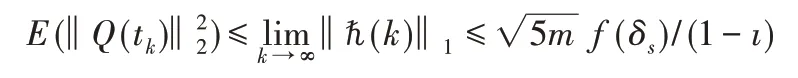
因此，存在正的常数a＞0和b＞0，使得

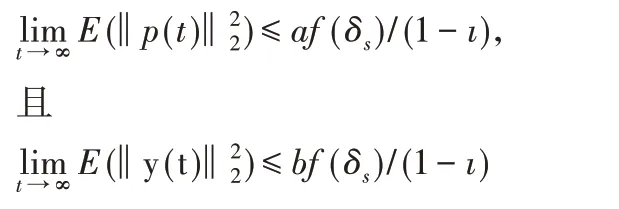
也就是说

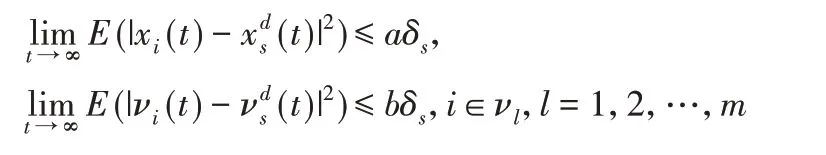
很明显，不等式右边为函数δs的单调递增函数。由定义2可知，系统（1）可以实现多追踪。

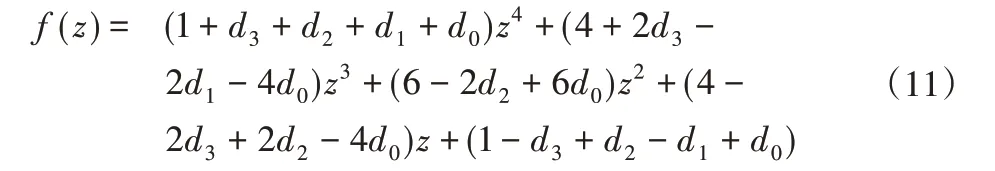
其中，

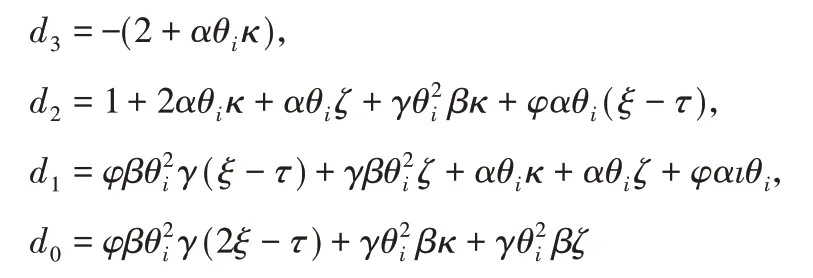
证明：矩阵A的特征多项式为：

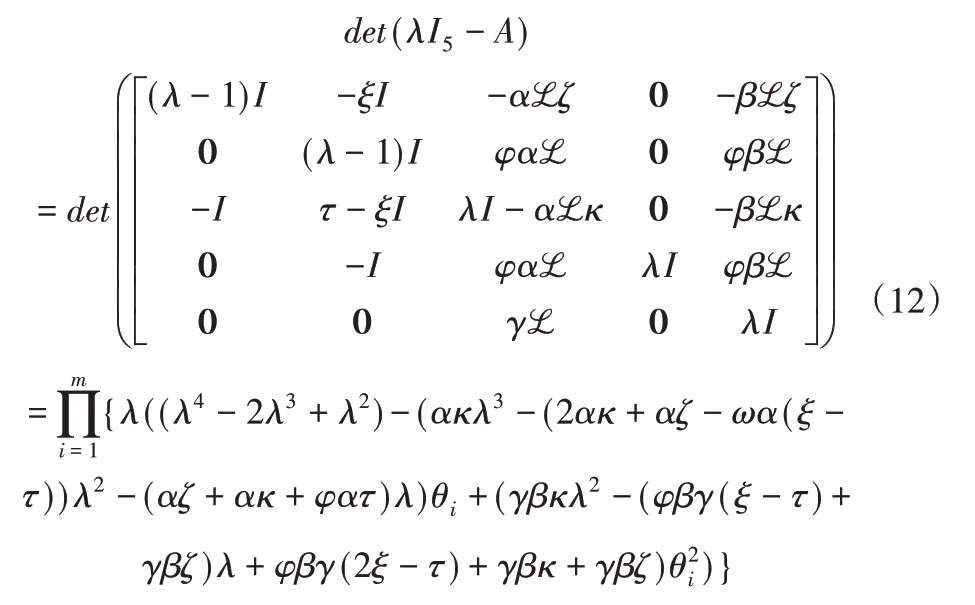
矩阵A的特征值满足：

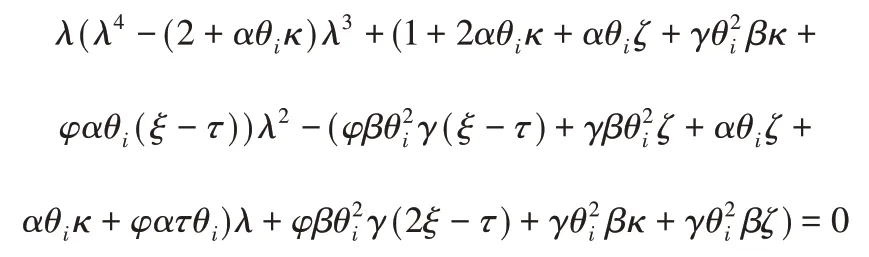
不难发现，对每个给定的θi，都可得五个矩阵A的特征值，其中0为一个特殊的特征值。为了简化计算，令

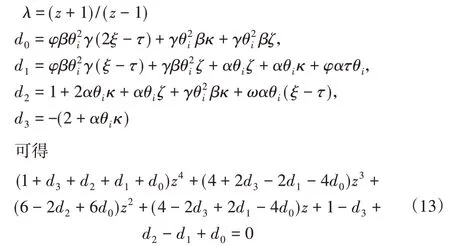
不难发现当且仅当R(z)＜0时ρ(A)＜1，也就是说二阶多智能体系统可以渐进到达多追踪当且仅当多项式（13）时Hurwitz稳定的。

4 案例分析

我们采用具有五个智能体的多智能体网络，测试所提出的通信时滞下的量化间歇控制协议。网络的拓扑图，如图1所示。将此网络G划分为两个子网络，两个子网络分别为：V1={1，2，3}和V2={4，5}。

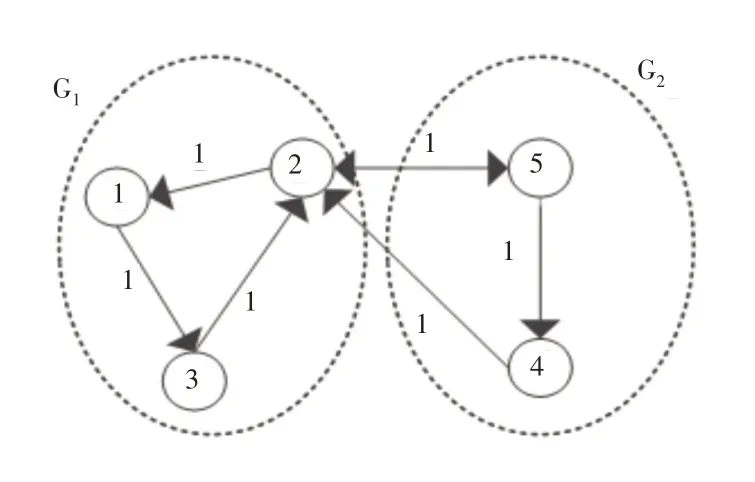
图1 具有5个节点的多智能体系统的拓扑图Fig.1 The Topology Diagram of a Multi-Agent System with 5 Nodes

牵制矩阵为B=[0，1，0，0，0；0，0，0，0，1]，也即牵制节点分别为节点2和节点5。Laplacian矩阵L为：

令脉冲函数为η(t)=1，通信时滞为τ=0.05，控制持续时间为ε=0.001，期望轨迹为。选择控制参数α=5，β=0.4和γ=2。从定理1可得，系统可以现实多追踪当且仅当0.1 ＜ξ＜3.5。基于控制协议（4），考虑通信时滞为τ，ξ=3.4时二阶多智能体系统（1）可以实现多追踪，如图2所示。ξ=3.5时二阶多智能体系统（1）可以实现多追踪，如图3所示。

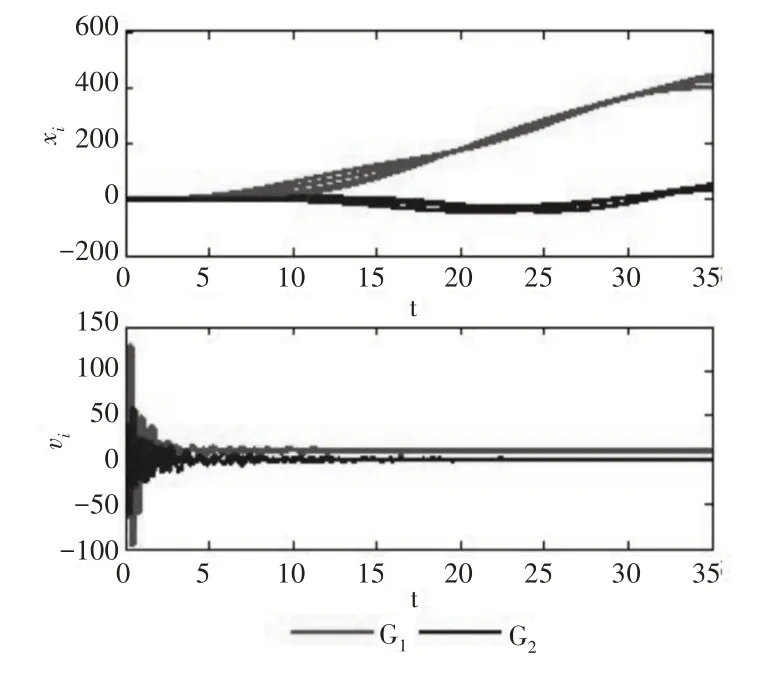
图2 ξ=3.4时通信时滞下的多智能体系统的多追踪轨迹。Fig.2 The Multi-Tracking Trajectory of Multi-Agent System Under Communication Time Lag ξ=3.4

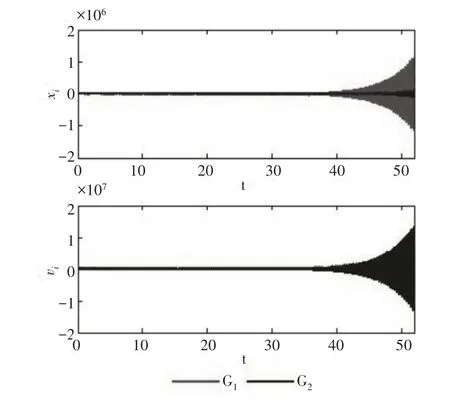
图3 ξ=3.5时通信时滞下的多智能体系统的多追踪轨迹。Fig.3 The Multi-Tracking Trajectory of Multi-Agent System Under Communication Time Lag ξ=3.5.

5 结论

针对通信时滞存在下的二阶多智能体的多追踪问题，提出了一个间歇控制协议，此控制协议中每个智能体的控制仅基于采样位移信息。为了克服通信带宽的限制，在信息传输前，采取随机量化的方案量化智能体的信息。基于代数图论、随机量化和稳定性理论，分析得到了实现系统多追踪的一些充分必要条件。仿真研究表明，所提出的控制协议可以保证每组中的智能体状态趋同于领导者的轨迹，另一方面不同组之间互不影响。最后，数值案例研究证实了所提出的间歇控制协议的有效性。将来，我们将考虑不同通信时滞的范围，完善系统的多追踪问题，提出的控制方案也可以应用于更多的案例。