王佩，李明昕

(1.广东金融学院，广东 广州 510521；2.内蒙古科技大学 理学院，内蒙古 包头 014010)

从理论上讲，在一个没有摩擦的金融市场中，两种资产和在未来某一固定时刻应具有相同或几乎相同的未定权益.因此，它们会以相同或接近相同的价格进行交易.然而，真正的金融市场并非毫无摩擦.因此，这对资产之间可能存在显著的定价差异，这种现象被称为“定价误差”.在现实中存在很多定价误差的例子，例如一些在中国证券交易所以A股，而在香港证券交易所以H股上市的中国公司就存在定价误差：主要包括中国银行和中国农业银行.根据惯例，即使只有一个价格偏离资产的正常价格水平，就可以认为定价较高的资产被(相对)高估，而定价较低的资产被(相对)低估.这两种资产在未来的某个时刻(可能是预先确定的)的价格应该相等，因此利用这种定价误差套利的常见策略采取“Long-Short”(以下简称L-S)策略.L-S策略持有相同规模的投资组合权重或股票数量，但符号相反，参见Mitchell M等[1]与Liu J等[2].

虽然L-S策略在业界和学术界都被广泛使用，但其设计目的是利用长期套利机会，却忽视了对短期多元化收益的探索.为了最优地利用定价误差，Liu J等[3]将其置于最大化投资组合框架下，进而推导出投资者的最优策略.他们发现，最优策略并不总是L-S策略.Yi等[4]进一步考虑了股票具有随机风险溢价和定价误差时，最优投资组合选择问题.他们发现，与Liu J等[3]的结果不同，在随机风险溢价下，即使股票的流动性相同，投资者的最优投资策略也不是L-S策略.在Liu J等[3]和Yi B等[4]的启发下，Gu A L， Gu A L等[5，6]分别考虑了无随机风险溢价和随机风险溢价下带有定价误差的最优投资再保险策略.

但目前有关带有定价误差的最优投资组合选择问题仅局限在终端财富期望效用最大化的假设下进行，没有控制投资组合的风险.因此，在均值-方差准则下研究带有定价误差的最优投资组合选择问题更符合实际需要.然而均值-方差目标函数中的方差项不满足期望迭代性质，Bellman最优性原则不再成立，从而导致均值-方差优化问题是一个时间不一致问题，即在初始时刻得到的最优策略在未来时刻不再是最优的.然而，投资策略的时间一致性是理性投资者的基本要求.如果投资策略缺乏时间一致性，投资者可能会遭受意想不到的损失.投资者更偏好对每个时间点都是最优的时间一致性策略，而不是仅在初始时间最优的预先承诺策略.因此，在Björk T[7]提出的博弈论框架下，大量的学者试图通过求解扩展Hamilton-Jacobi-Bellman(HJB)方程系统研究均值-方差准则下的时间一致投资策等和略(也称均衡策略)，参见Björk T等[8]、Zeng Y[9]等和Li Y[10]等.

因此，本文在均值-方差准则下，研究具有定价误差和随机风险溢价的投资组合选择问题.具体地，金融市场包含一个无风险资产，一个市场指数和一对错误定价的股票，其中市场指数和股票的价格过程均满足几何布朗运动，而股票具有服从均值回复过程的随机风险溢价.投资者的决策目标是最大化终端财富期望的同时最小化终端财富的方差.在博弈论的框架下，得到均衡投资策略和相应值函数的解析式.然后利用数值算例分析了模型参数对均衡投资策略和均衡有效前沿的影响.

1 模型构建

设(Ω，F，Q)一个赋流的完备概率空间，具有信息域流{Ft}0≤t≤T，其中Ft为t时刻t金融市场中的信息，[0，T]为固定有限的投资期限.假设文中所有的随机过程均为{Ft}0≤t≤T适应的.

1.1 金融市场

假设金融市场由一个无风险资产、一个市场指数和一对存在定价误差的股票.无风险资产的价格过程S0(t)为：

(1)

式中：r>0为无风险利率.市场指数的价格过程Pm(t)满足如下随机微分方程：

(2)

式中：μm>0为市场风险溢价，σm为市场波动率，Zm(t)为一维标准布朗运动.一对存在定价误差的股票价格过程P1(t)，P2(t)满足如下随机微分方程：

(3)

(4)

式中：l1，l2，σ>0，β>0为常数，Z(t)，Z1(t)，Z2(t)为3个一维标准布朗运动，且Zm(t)，Z(t)，Z1(t)，Z2(t)彼此相互独立.σdZi(t)为2支股票的共同风险，βdZi(t)为第i支股票的特质风险，μ(t)为2支股票共同风险σdZ(t)的溢价，其动态演化过程满足如下均值回复过程：

(5)

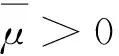
(6)

dX(t)=-(l1+l2)X(t)dt+bdZ1(t)-bdZ2(t)

=(l1+l2)(0-X(t))dt+bdZ1(t)-bdZ2(t) .

(7)

式(7)表明定价误差X(t)也服从一个均值回复过程，其长期均值为0，均值回复速度为l1+l2.为了方便起见，假设l1+l2>02.li可表示第i支股票的流动性，i=1,2.事实上，定价误差一般发生在具有摩擦的金融市场，而市场摩擦很大程度上是源于市场流动性不足.当流动性l1,l2较小时，定价误差X(t)需要较长的时间才能回复到零均值，这与流动性越低，市场摩擦越大的观点是一致的.

1.2 财富过程

令π={(πm(t),π1(t),π2(t)),0≤t≤T}为投资策略，其中πm(t),π1(t),π2(t)分别表示时刻t投资到市场指数和2支股票的财富比例，则1-πm(t)-π1(t)-π2(t)为时刻投资到无风险资产的财富比例.因此，投资者采用投资策略π时的相应财富Wπ(t)满足如下动态过程：

(8)

同时，假设Wπ(0)=w0,X(0)=x0,μ(0)=π0.

定义1：(容许策略)称策略是一个容许策略π={(πm(t),π1(t),π2(t)),t∈[0,T]}，如果

(Ⅱ)对任意(t,w,x,μ)∈[0,T]×O，O=+××，方程(8)式有唯一强解.

所有允许策略组成的集合记为Π.

1.3 优化问题

假设投资者的目标是终端财富越多的同时风险越小.也就是说投资者在投资期末T的财富水平达到最高且风险最低.投资者的这一目标可用下面的均值-方差模型表示：

(9)

式中：γ为投资者的风险厌恶程度，Et,w,x,μ[·]=E[·|Wπ(t)=w,X(t)=x,μ(t)=μ]和Vart,w,x,μ[·]=Var[·|Wπ(t)=w,X(t)=x,μ(t)=μ]分别为给定Wπ(t)=w,X(t)=x,μ(t)=μ下的条件期望和条件方差.另外，J(t,w,x,μ)可写为：

=Et,w,x,μ[F(Wπ(T))]+G(Et,w,x,μ[Wπ(T)])

本文将在Björk T[7]等提出的博弈论框架下求解时间不一致优化问题(9)，并寻找其时间一致的均衡投资策略.下面首先定义优化问题(9)的均衡策略.

定义2：(均衡策略)称一个容许策略π*是优化问题(9)的均衡策略，如果对所有给定的π∈Π，h>0，和(t,w,x,μ)∈[0,T]×O，下式成立

式中：πh为

πh(s,y)=

则优化问题(9)的均衡值函数为

V(t,w,x,μ)=J(t,w,x,μ,π*)

2 均衡投资策略

下面利用Björk J等[7]的结论推导优化问题(9)满足的扩展HJB方程系统.为了方便起见，定义

C1,2,2,2([0,T]×O)={Ψ(t,w,x,μ)|Ψ(t,·,·,·)在[0，T]上一阶连续可微，Ψ(·,w,x,μ)分别关于w在+，x在，μ在上二阶连续可微} .

对任意Ψ(t,w,x,μ)∈C1,2,2,2([0,T]×O)，定义微分算子Aπ：

式中：Ψt,Ψw,Ψx,Ψμ,Ψww,Ψxx,Ψμμ,Ψwx,Ψwμ分别为Ψ(t,w,x,μ)关于相关变量偏导数的简写，πm,π1,π2分别为πm(t),π1(t),π2(t)的简写.

根据Björk T[7]等中的扩展HJB方程系统与相应验证定理，可知优化问题(9)的均衡投资策略π*和相应的均衡值函数V(t,w,x,μ)可通过求解如下扩展HJB方程系统和验证定理得到.

定理1：(验证定理)假设存在实值函数V(t,w,x,μ)，g(t,w,x,μ)∈C1,2,2,2([0,T]×O)满足如下的扩展HJB方程系统：

(10)

其中上式中第一个方程的极大值在π*实现，G◇g，Hug定义为

(G◇g)(t,w,x,μ)=G(g(t,w,x,μ)) ,

Hπg=Gy(g(t,w,x,μ))Aπg(t,w,x,μ) ,

则g(t,w,x,μ)=Et,w,x,μ[Wπ*(T)]，π*为优化问题(9)的均衡投资策略，V(t,w,x,μ)是相应的均衡值函数.

证：该定理的证明类似于Björk T[7]等中定理4.1的证明，这里省略.

为了求解优化问题(9)的均衡策略和相应均衡值函数，对扩展HJB方程系统(10)进行化简，得到如下命题.

命题1：扩展HJB方程系统(10)可化简为

(11)

(12)

(13)

证：该定理的证明类似于Li Y等[10]，故略去.

通过求解化简的扩展HJB方程系统(11)～(13)，可得优化问题(9)的均衡策略和相应均衡值函数的解析表达式.猜测函数V(t,w,x,μ)和g(t,w,x,μ)具有如下形式：

(14)

Vw=A1,Vww=0,Vx=A2x+A3+B3μ,Vxx=A2,

Vμ=B1μ+B2+B3x,Vμμ=B1,Vxx=Vμμ=0 ,

(15)

和

(16)

根据一阶最优条件，对方程(15)分别关于πm,π1,π2求导，得到

(17)

将(17)式代入(15)，(16)式，并关于w，x2，x，μ2，μ，xμ及剩余项进行整理，可得

(18)

和

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

将(20)～(32)式分别代入(14)与(17)式，即可得均衡值函数、期望的终端财富与均衡投资策略π*.将结果总结为如下命题.

定理2：具有财富过程(8)均值方差优化问题(9)的均衡投资策略为

其中

(33)

相应的均衡值函数为

(34)

预期的终端财富为

g(t,w,x,μ)=Et,w,x,μ[Wπ*(T)]

(35)

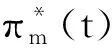
(36)

(37)

则有

(38)

注2：根据定义1、定理2和优化问题(9)的定义，可知给定初始条件(w0,x0,μ0)下，优化问题(9)在时刻t=0的均衡有效前沿为

3 数值算例

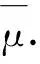
3.1 均衡策略的敏感性分析

本文主要关注股票随机风险溢价和其均值回复速度κ，定价误差x及其均值回复速度l1+l2对均衡投资策略的影响.若假设x>0且l2>l2>0，则第一支股票价格被高估而第二支股票价格被低估，并且被低估的股票回复到均值的速度比被高估的股票回复到均值的速度快.因此，买入低估股票的优势会以更快的速度消失.l1和l2的相对大小以及x与0的相对大小有很多可能的组合，都可以进行相应地解释和分析，本文不再详述.

图1 μ对均衡投资策略的影响

图2 x对均衡投资策略的影响

图3，4显示了股票随机风险溢价的均值回复速度κ和定价误差的均值回复速度l1+l2对πL-S的影响.图3表明πL-S随κ的增大而增大，图4表明πL-S关于l1+l2也是递增的.但通过比较图3，4可发现，πL-S对l1+l2的变化更为敏感，而对κ的变化不太敏感.当l1=l2时，2支股票流动性相同，则πL-S与κ无关.πL-S体现了2支股票的流动性差异以及定价误差.均值回复速度κ会改变股票的流动性，因此对πL-S有影响，但当2支股票的流动性差异为零时，这种影响消失.因此，投资者利用定价误差的套利优势时，应关注市场流动性的变化.

图3 κ对πL-S的影响

图4 l1+l2对πL-S的影响

图5，6显示了股票随机风险溢价的均值回复速度κ和定价误差的均值回复速度l1+l2对均衡有效前沿的影响.由图5可知，随着κ的增长，股票随机风险溢价μ(t)的不确定性越小，故当终端财富的期望水平相同时，终端财富的方差越小，也就是说投资风险降低.图6表明，当l1+l2增大，定价误差X(t)的不确定性降低，因此终端财富的期望水平相同时，终端财富的方差减小.

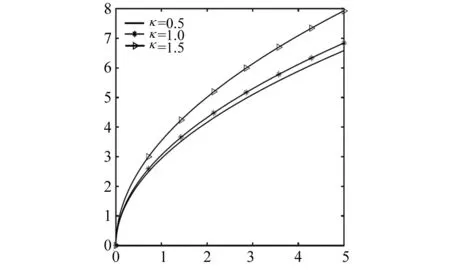
图5 κ对均衡有效前沿的影响

图6 l1+l2对均衡有效前沿的影响

4 结论

研究了股票存在定价误差且具有随机风险溢价时，使投资者终端财富均值-方差效用最大的均衡投资策略.股票的随机风险溢价和定价误差都遵循均值回复过程.利用Björk T[7]等提出的博弈论思想，得到了均衡投资策略以及相应值函数的解析式.通过数值算例分析了随机风险溢价和定价误差对均衡投资策略及均衡有效前沿的影响.结果表明，市场流动性会影响对定价误差的对冲需求，并且市场流动性增强会降低投资组合风险.