李 雪 张琳玮 姜 涛 陈厚合 李国庆

（东北电力大学电气工程学院 吉林 132012）

0 引言

交直流电网互联规模不断扩大、可再生能源大规模并网，在改善电网大规模电能输送能力和优化电源结构的同时，也使电力系统运行中随机性和不确定性因素日益增加，给电力系统电压稳定性带来诸多挑战[1-5]。因此，研究各种随机性和不确定性因素影响下的电力系统电压稳定性对电力系统安全稳定运行具有极其重要的意义[6-9]。

静态电压稳定域（Static Voltage Stability Region,SVSR）是分析和评估电力系统电压稳定性的重要工具[10-13]，它已在研究强随机性和不确定性因素影响下的电力系统电压稳定性中发挥了巨大的作用，但构建SVSR关键在于对其边界的搜索。超平面近似作为目前最为通用的静态电压稳定域边界（Static Voltage Stability Region Boundary,SVSRB）构建方法，已在工程中得到了应用[14-16]。该方法核心思想是在功率注入空间内搜索系统所有可能运行方式下的鞍结分岔（Saddle Node Bifurcation,SNB）点，借助这些SNB点来近似SVSRB。因此，构建SVSRB关键是对SNB点的快速、准确搜索。

目前，电力系统SNB点的搜索方式主要有连续潮流（Continuation Power Flow,CPF）法[17-18]、最优潮流（Optional Power Flow,OPF）法[19]和直接法[20-21]。CPF法以系统当前运行点为始点，沿指定功率增长方向采用预测-校正方式追踪系统SNB点，该方法虽可获得较高精度的SNB点，但系统规模会严重制约该方法的计算效率。OPF法以系统负荷裕度最大为目标函数、潮流方程为约束条件，通过求解该优化模型获得电力系统的SNB点，但优化算法需要通过寻优以逐次逼近最优解，其求解过程相对耗时，且“维数灾”问题难以解决，不利于区域互联电力系统SNB点的快速搜索。直接法通过求解一组表征SNB点特性的非线性方程组来搜索SNB点，该方法对初值较为敏感且计算量较大，系统规模的扩大会导致该方法的计算量和存储空间急剧增加，故该方法也难以适用于大规模区域互联电力系统SNB点的快速搜索。为提高SVSRB的搜索效率，文献[22-23]分别提出了基于边界追踪的预测-校正算法和基于边界追踪的优化算法，以实现SVSRB的快速构建。但如何在实现区域互联电力系统SVSRB高精度构建前提下，进一步提高SVSRB的计算效率仍具有十分重要的研究价值。

相对于CPF法和OPF法，直接法通过求解一组表征SNB点特性的非线性方程组便可获取系统的SNB点，该方法计算原理简单、计算精度高，且在求解SNB点时涉及大量的线性方程组计算，虽然其方程组的计算量和计算复杂度较高，但易于通过GPU并行加速以提高SVSRB计算效率[24]。因此，本文以直接法为基础，提出一种基于CPU-GPU异构的电力系统静态电压稳定域边界并行计算方法。该方法依据SVSRB拓扑性质，采用沿边界追踪SVSRB的搜索方式，将已求SNB点处系统信息作为直接法搜索相邻SNB点的初值，以克服直接法对初值敏感的不足；再结合CPU-GPU异构平台实现SNB点的并行求解，以降低直接法计算量大、计算复杂度高的缺陷，从而提升SVSRB搜索效率；最后通过多组测试系统算例，对所提SVSRB并行计算方法的准确性和有效性进行分析、验证。

1 基于直接法的鞍结分岔点计算方法

由文献[25-27]可知，电力系统的SVSRB主要是由SNB点和极限诱导分岔（Limit Induced Bifurcation,LIB）点构成的，而LIB点可在SNB点搜索的基础上，利用参考文献[28]来判断是否到达，因此，SNB点的搜索至关重要。本文在构建SVSRB时重点关注SNB点的搜索，将SVSRB的搜索等效为搜索系统在各种可能运行方式下的SNB点。而直接法作为一种求解SNB点的常用方法，其原理简单，便于计算，已被用于电力系统SNB点的求解[20-21,28]。因此，本文采用直接法来搜索电力系统的SNB点。

1.1 直接法基本原理

直接法搜索电力系统SNB点的核心思想就是求解一组能够反映系统SNB点特性的非线性方程组，该非线性方程组的表达式为

式中，f(x,λ)=0为含参数的潮流方程，x为状态变量，l为负荷裕度；fx(x,λ)·r=0为潮流方程所对应Jacobi矩阵发生奇异的方程，fx(x,l)为潮流Jacobi矩阵，r为零特征值所对应的右特征向量，其维度与潮流方程一致；rp-1=0为规范化方程，rp代表r中的第p个元素。对于一给定电力网络，若系统总节点数为N，PQ节点共npq个，PV节点共npv个，令n=2npq+npv，则上述非线性方程组的维度为2n+1。

采用直接法求解电力系统SNB点的过程，实质就是采用牛拉法求解式（1）所示的非线性方程组，其求解过程中的修正方程组为

式中，fxxr∈Rn×n，其任意第l行、第d列的元素可表示为，其第p个元素为1，其余元素均为0；fλ∈Rn为含参数的潮流方程对λ的偏导数。

由式（2）可求得修正量Δx、Δr和Δl，将所得修正量代入式（3）更新变量x、r和l。

设定收敛阈值ε，将式（3）更新后的x、l和r代入式（1），若满足收敛条件‖f(x,l)‖≤ε和‖fxr‖≤ε，则迭代完成，SNB点处x、r和l求解完毕；否则，继续迭代，直至f(x,l)和fxr满足上述收敛条件为止。

1.2 修正方程组的降阶处理

由式（2）可知：修正方程组式（2）的维数是潮流方程维数的两倍，在迭代求解过程中，计算量较大，导致整个SNB点的求解耗时较高。为降低式（2）中修正量求解的复杂度和计算量，文献[20]将式（2）所示的2n+1维修正方程组通过换元变换拆分成式（4）～ 式（7）所示的四组同系数n+1维线性方程组。

各修正量与α、β、ξ和η关系为

式中，Δxp为薄弱节点电压幅值变化量，用于临界点处x、r和l的初值预测，其计算公式为

通过求解降阶后的线性方程组式（4）～式（7），并根据式（8）所示各修正量与α、β、ξ和η的关系，先求解修正量Δx、Δr和Δl，然后将Δx、Δr和Δl代入式（3），可对待求变量x、r和l进行修正，以提高修正量求解效率，减少数据所需存储空间，提高直接法搜索SNB点的计算效率。

2 基于直接法的SVSRB并行计算

采用第1节所述的直接法在功率注入空间内搜索大量SNB点，并借助这些SNB点即可近似系统SVSRB。然而，直接法对初值非常敏感，若采用传统的SVSRB搜索方法（简称“射线法”），不当的初值选取可能导致直接法求解结果不收敛或收敛耗时较长。同时，系统规模的扩大将导致直接法的计算量急剧增加，不利于大规模电力系统SVSRB的快速搜索。针对上述不足，本文提出一种基于边界追踪的直接法以实现SVSRB的并行计算。

2.1 基于边界追踪的直接法

边界追踪法的核心思想是利用SVSRB上相邻SNB点的系统运行信息变化较小这一特点，将已求SNB点的状态量x、右特征向量r和负荷裕度l作为下一相邻待求解SNB点的初值，以充分利用各SNB点信息，提高SVSRB构建效率。基于该思想，本文将直接法与边界追踪法相结合，提出一种基于边界追踪的SVSRB快速搜索的直接法，以有效利用各SNB点的系统运行信息，克服直接法初值选取困难的不足。由于基于边界追踪的直接法可以很好地保证求解SNB点时给定初值的精度，因此，有利于加快直接法计算SNB点的收敛速度，提高SVSRB的搜索效率。

图1给出了基于边界追踪的直接法搜索SVSRB的基本原理。首先给定初始功率增长方向d0，d0对应的功率增长方向角q0=arctan(ΔPj0/ΔPi0)，ΔPi0、ΔPj0分别为d0中对应于节点i、j的功率注入增长分量。以基态为起始点，根据近似二次曲线预估SNB点初值[20]，采用第1节所述的直接法计算功率增长方向d0下的SNB点0，SNB点0处的状态变量、负荷裕度和右特征向量分别为x0、l0和r0。改变d0中节点i、j的有功注入增长分量ΔPi0和ΔPj0，得到新功率增长方向d1为

图1 基于边界追踪的SVSRB搜索示意图Fig.1 Exploring SVSRB using boundary tracking method

2.2 直接法并行计算SVSRB的预处理

采用边界追踪的直接法很好地解决了直接法搜索电力系统SNB点时初值选取困难这一瓶颈。然而，直接法求解SNB点时，牛顿迭代修正方程组式（2）的维数是潮流方程组维数的两倍，计算量大、计算复杂度高，严重影响了SVSRB构建效率。尽管对修正方程组式（2）的降阶处理有效降低了修正方程组维数，但降阶处理使得需要求解的线性方程组数量增多，搜索SNB点的计算量依然很大，不利于SNB点的快速搜索。为此，本文基于CPU-GPU异构平台，将直接法求解式（4）～式（7）的四组n+1维线性方程组采用带Jacobi+ILU(0)两阶段预处理的稳定双共轭梯度法（BICGSTAB）进行求解，并借助GPU对该求解过程进行并行加速，以降低直接法搜索电力系统SNB点的计算量和复杂度，提高SVSRB搜索效率。

利用GPU的并行计算能力加速迭代法求解线性方程组是GPU的主要应用之一[29-31]，借助GPU的并行计算优势，并根据系数矩阵B既不对称也不正定，且具有高度稀疏性的特点，参考文献[24]，本文采用Jacobi预处理与ILU(0)预处理相结合的Jacobi+ILU(0)两阶段预处理方法，并结合BICGSTAB迭代法求解线性方程组式（4）～式（7），以提高修正量求解速度。

以式（4）为例，本节简要介绍Jacobi+ILU(0)预处理的BICGSTAB迭代法求解过程。将线性方程组式（4）简记为

式中，B为系数矩阵；α为待求向量；b为等式右侧列向量。对式（12）进行Jacobi+ILU(0)预处理，处理后的线性方程组等效为

式中，J为Jacobi预处理矩阵；L、U分别为ILU(0)分解得到的上、下三角稀疏矩阵。选取L为预处理矩阵，对式（13）进行变换，得到

2.3 基于直接法的SVSRB并行计算流程实现

采用基于BICGSTAB迭代法和Jacobi+ILU(0)两阶段预处理的线性方程组求解方法可以加快式（4）～式（7）的求解效率。为进一步提升直接法搜索SNB点的计算效率，本文采用CPU-GPU异构平台，将直接法搜索SNB点过程中计算量较大、计算耗时占比高的修正量求解部分由GPU完成，即借助GPU的并行加速技术对BICGSTAB迭代法进行加速求解，以提高修正量的求解效率，而其他逻辑性较强，计算量较小部分由CPU完成。具体而言，在CPU中，通过牛拉法对表征SNB点特性的非线性方程组式（1）线性化处理，得到相应的修正方程组式（2），并对式（2）进行降阶处理，得到如式（4）～式（7）所示的四组同系数线性方程组；然后将系数矩阵B、线性方程组（4）～式（7）右侧列向量、生成的预处理器J、L和U，以及其他相关参数从CPU移植到GPU中，在GPU中，采用带Jacobi+ILU(0)两阶段预处理的BICGSTAB迭代法对式（4）～式（7）进行并行求解，得到α、β、ξ和η；接着将α、β、ξ和η传输到CPU中，在CPU中，利用各修正量与α、β、ξ和η的关系，由式（8）得到修正量Δx、Δr和Δl，并按式（3）对待求量x、r和l进行修正，将修正后的x、l和r代入式（1），重复牛顿迭代过程，直到f(x,l)和fxr满足‖f(x,l)‖≤ε和‖fxr‖≤ε，则迭代完成，x、r和l求解完毕，至此，则可实现SNB点并行求解，从而提高SVSRB的搜索效率。

图2进一步给出了二维有功注入空间内所提基于CPU-GPU异构的静态电压稳定域边界并行计算的流程。

图2中采用CPU-GPU异构平台计算SNB点的具体过程如前所述，牛顿迭代求解SNB点的初值x0、l0和r0由SVSRB上相邻已求SNB点的系统运行信息给定。因SVSRB上相邻SNB点距离较近，系统运行信息变化较小，故采用基于边界追踪的直接法可以保证直接法搜索SNB时对初值的高质量选取，有利于加快直接法搜索SNB点的收敛速度，克服直接法初值不易选取的不足；而对于直接法计算量大、计算复杂度高这一缺陷，采用CPU-GPU异构平台，利用GPU并行技术对直接法搜索SNB点时计算量较大的四组同系数线性方程组式（4）～式（7）进行并行加速求解，大幅降低了直接法搜索SNB点的计算量与计算复杂度。上述两种处理方式的有机结合，有效解决了直接法初值敏感、计算量大这两大不足，实现了SVSRB上各SNB点的快速并行求解。

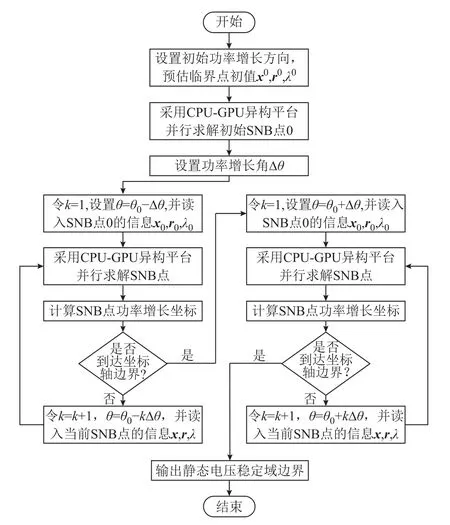
图2 基于CPU-GPU异构的SVSRB并行计算流程Fig.2 Flow chart of the proposed CPU-GPU heterogeneous computing method

在搜索出SVSRB基础上，为进一步获取SVSRB近似解析表达式，以指导电网运行人员进行电压稳定性评估与控制，可参考文献[25]，再对SVSRB进行近似，得到SVSRB的近似解析表达式。

3 算例分析

针对所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法，本节首先以WECC3机9节点系统为例，验证本文所提方法的准确性；然后以欧洲13659节点系统为例，验证所提方法构建区域互联电力系统 SVSRB 的可行性；最后以case2737sop、case3120sp、case7092、case9241pegase等多个测试系统为例，验证所提方法的有效性。

本文算例计算硬件平台为 Dell PowerEdge C4130机架式服务器，CPU为Inter Xeon E5-2690，主频2.6GHz，内存256GB，GPU为Nvidia Tesla K80，总内存带宽480GB/s。软件平台为Matlab2018a，CUDA驱动版本为8.0。构建SVSRB时控制搜索方向的功率增长角Δq为0.1rad，牛顿-拉夫逊法的收敛精度ε取10-2，最大迭代次数N取50，BICGSTAB迭代法的收敛阈值εb取10-2。

3.1 WECC3机9节点测试系统

本节首先以WECC3机9节点系统为例[32]，采用所提SVSRB并行计算方法，分别构建二维、三维有功功率注入空间内的SVSRB。

3.1.1 二维SVSRB构建

选择节点5、7的有功注入量为坐标轴，在以节点5、7形成的二维负荷有功注入空间内采用本文所提方法构建SVSRB，如图3所示。

图3 WECC-9系统的SVSRBFig.3 SVSRB of WECC-9 test system

由图3可知：首先，以基态为起始点，设置追踪第一个SNB点时所对应的功率增长方向d8=[0 0.326 0 0.170 0 0 0.180 0 0 0.200 0 0 0]T，d8对应的功率增长方向角q8=0.732 8rad，采用CPUGPU异构平台并行求解d8下的SNB点。具体过程如下：通过牛拉法对式（1）线性化处理并对牛顿迭代修正方程组式（2）进行降阶处理，得到式（4）～式（7）；然后，将系数矩阵B、线性方程组式（4）～式（7）右侧列向量、预处理器J、L和U，以及其他相关参数从CPU移植到GPU中，并利用GPU的并行加速技术，采用带两阶段预处理的BICGSTAB迭代法并行求解式（4）～式（7），得到中间变量α、β、ξ和η；再将求解的α、β、ξ和η传输到CPU中，利用各修正量与α、β、ξ和η的关系得到修正量Δx、Δr和Δl，并按式（3）对待求量x、r和l进行更新；重复上述过程，直到满足牛顿迭代收敛条件，则d8下的SNB点并行求解完毕，得到的初始SNB点如图3中SNB点8所示，其坐标为（2.388 0,2.149 2），最大负荷裕度l8=11.939 8(pu)。

然后，沿q减小方向采用基于边界追踪的直接法并行搜索系统SNB点，详细过程如下：以SNB点8为起始点，令q7=q8-Δq，根据d8中节点5、7的有功增长分量ΔP5、ΔP7及q7得到新的功率增长方向d7=[0 0.326 0 0.170 0 0 0.159 1 0 0.217 0 0 0]T；以SNB点8的状态变量x8、负荷裕度l8及右特征向量r8作为直接法搜索d7下SNB点的初值，采用CPU-GPU异构平台实现SNB点的并行求解，得到d7对应的SNB点7，SNB点7的坐标为（2.661 2,1.951 8），最大负荷裕度l7=12.265 4(pu)。以此类推，将已求SNB点作为相邻待求解SNB点的起始点，其状态变量、负荷裕度和右特征向量作为直接法搜索相邻待求解SNB点的初值，并结合CPU-GPU异构平台实现SNB点的并行求解，依次得到SNB点6,5,4,…,0，其中SNB点0的功率增长方向角q0=-0.067 2rad，此时q0＜0，令q0=0，计算d0=[0 0.326 0 0.170 0 0 0 0 0.269 1 0 0]T下的SNB点0，并停止沿q减小方向SNB点的搜索。

进一步，仍以SNB点8为起始点，类似上述过程，沿q增大的方向采用CPU-GPU异构的直接法依次搜索SNB点9,10,11,…,17，SNB点17的功率增长方向角为q17=1.632 8rad，此时有：q17＞π/2，令q17=π/2，计算d17=[0 0.326 0 0.170 0 0 0.269 1 0 0 0 0]T下的SNB点17，至此，系统在第一象限内沿q增大方向的SΝΒ点搜索结束。各SΝΒ点详细信息见表1。将图3搜索得到的SΝΒ点依次连接，即可获得由节点5、7形成的二维有功注入空间内的SVSRB。

表1 WECC-9系统中各SNB点信息Tab.1 Detailed information of SNB of WECC-9 test system

图3进一步对比了本文所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法与CPF法、基于射线的直接法、基于边界追踪的直接法所构建的SVSRB。由图3可知：对于同一个功率增长方向，本文提出的SVSRB并行计算方法获得的SNB点和CPF、基于射线的直接法、基于边界追踪的直接法得到的SNB点近似重合，有效验证了所提的静态电压稳定域边界并行计算方法的准确性。

由于SNB点处潮流方程所对应的Jacobi矩阵发生奇异，Jacobi矩阵存在零特征值，故搜索得到的SNB点处Jacobi矩阵对应的最小特征值到0的距离可以作为衡量各种方法计算精度的标准。

图4分别对比了CPF、基于射线的直接法、基于边界追踪的直接法和本文所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法得到的SNB点处潮流Jacobi矩阵所对应的最小特征值。由图4中各SNB点处的最小特征值可以看出：本文所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法与基于射线的直接法、基于边界追踪的直接法计算得到的SNB点精度较CPF法搜索的SNB点精度高。图4中由CPF法所得的SNB点平均最小特征值为1.04×10-2，而本文所提方法与基于边界追踪的直接法、基于射线的直接法获得的最小特征值的平均值分别为1.21×10-3、1.20×10-3、2.01×10-3，该三种方法计算得到的SNB点精度大致相等，且比CPF的计算精度高出一个数量级，该对比结果表明：本文所提静态电压稳定域边界并行计算方法具有较高的计算精度。

图4 SVSRB的计算误差Fig.4 Calculation errors of SVSRB

进一步，在图3搜索所得SVSRB基础上，参考文献[25]，对图3的SVSRB进行近似，近似结果如图5所示，对应的SVSRB局部近似边界H1、H2、H3、H4、H5、H6、H7、H8解析表达式如式（16）所示。

图5 WECC-9系统二维SVSRB的近似边界Fig.5 Approximated 2-dimensional SVSRB of WECC-9 test case

3.1.2 计算效率分析

本节进一步对比了CPF法、基于射线的直接法、基于边界追踪的直接法与本文所提方法在上述场景下的计算效率。

表2给出了上述场景下不同方法构建二维SVSRB的计算时间。由表2可知，CPF在上述场景下的计算耗时远大于基于射线的直接法、基于边界追踪的直接法和本文所提出方法的计算耗时；基于边界追踪的直接法在上述场景中的计算耗时较基于射线的直接法、CPF法分别减少了24.8%和94.7%；本文所提方法的计算时间较基于边界追踪的直接法、基于射线的直接法耗时更长。出现上述结果的原因是：CPF法获得SNB点时涉及大量的预测-校正过程，该过程相对耗时，且随着SNB点数量的增多，CPF的耗时明显增加，因而基于CPF的SVSRB构建方法用时较长；而本文所提方法与基于射线的直接法、基于边界追踪的直接法均是对表征SNB点特性的非线性方程组进行求解，获得SNB点的过程相对简单，且所需的牛顿迭代次数远小于CPF法校正步的总迭代次数，因而计算时间较CPF更短；但因测试系统较小，CPU与GPU数据交互的耗时远大于GPU并行求解带来的加速性，因而本文所提方法较基于边界追踪的直接法、基于射线的直接法耗时更久。

表2 不同方法的计算时间对比Tab.2 Computational times compared with different methods

由于直接法搜索电力系统SNB点的核心是利用牛拉法对式（1）进行求解，因此，构建SVSRB的计算耗时主要依赖于获取SNB点时的牛拉法总迭代次数。表3对比了本文所提方法与基于射线的直接法、基于边界追踪的直接法搜索SVSRB的迭代次数。

表3 不同方法的迭代次数Tab.3 Total times of iterations compared with different methods

由表3的对比结果可知：基于边界追踪的直接法搜索SVSRB时所需的总迭代次数较少，因而搜索SVSRB时计算耗时较少；基于射线的直接法搜索SVSRB所需总迭代次数较多，计算耗时较基于边界追踪的直接法更长；而本文所提方法虽有较少的迭代次数，但构建SVSRB所需的计算时间比基于射线的直接法和基于边界追踪的直接法更久。其主要原因是：基于射线的直接法始终以基态为起始点，各SNB点的搜索相对独立，且需不断利用负荷参数二阶导数预估不同功率增长方向下的SNB点的初值，因此获得SNB点收敛解所需的牛顿迭代次数较多，收敛耗时较长；而基于边界追踪的直接法将已求SNB点作为相邻待求解SNB点的初始点，因初值更接近待求解SNB点的真实值，故获取SNB点时所需的迭代次数更少，构建SVSRB的计算耗时更短；本文所提方法是在基于边界追踪的直接法基础上利用CPU-GPU异构平台进行的SVSRB并行计算，因而牛顿总迭代次数较少，但本文采用CPU-GPU异构平台求解SNB点时，由于测试系统规模较小，CPU与GPU间数据交互耗时远大于GPU并行加速的计算耗时，因而构建SVSRB计算时间相对较长。

3.1.3 功率增长角Δq的分析

由于SVSRB上获得各SNB点的功率增长方向受功率增长角Δθ的影响，Δθ过大或过小均会影响SVSRB的构建精度及构建速度。因此，本节进一步分析了Δθ对构建SVSRB的具体影响。

表4为不同Δθ时，在上述坐标空间中构建二维SVSRB所需计算耗时与牛拉法总迭代次数的对比。由表4可知：当Δθ＝0.05rad时，构建SVSRB所需的SNB点数量较多，故构建SVSRB时牛顿迭代的总迭代次数较多，计算耗时较长，但因相邻SNB点距离较近，因此平均迭代次数相对较少；当Δθ＝0.25rad时，构建SVSRB所需SNB点数量较少，故牛顿迭代法的总迭代次数相对较少，搜索SVSRB的计算耗时较短，但因相邻SNB点距离相对较远，因此牛拉法迭代时所需的平均迭代次数相对较多。

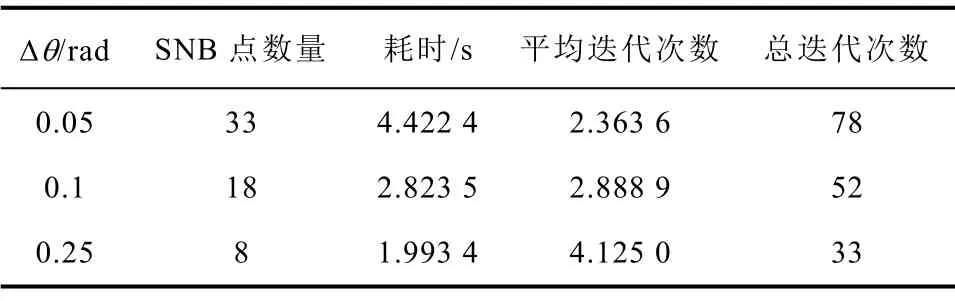
表4 不同Δθ 取值下的SVSRB计算效率对比Tab.4 Computational efficiency comparisons of SVSRB with different Δθ

随着Δθ的不断增大，构建SVSRB所需SNB点数量不断减少，计算时间也相对减少，但SVSRB的构建精度与所搜索的SNB点数量密切相关，搜索的SNB点数量越多，构建的SVSRB越准确。因而，Δθ的增大在提高SVSRB构建效率的同时，也降低了SVSRB构建精度。图6给出了在节点5、7形成的二维负荷有功注入空间内，由不同Δθ下构建的SVSR局部边界。由图6可知，Δθ取0.1rad时，SVSR区域由A、B和C三部分组成，Δθ取0.25rad时，SVSR区域由A组成。显然，由区域A、B和C共同组成的区域更加接近真实的SVSR。Δθ取0.25rad时得到的SVSR区域较为保守，当系统运行在区域B或C时，会造成系统误报警，因此，Δθ的取值需在SVSRB的搜索精度和搜索效率之间达到平衡。对比表4和图6的计算结果可知：本文中Δθ取值为0.1rad是合理、可行的。

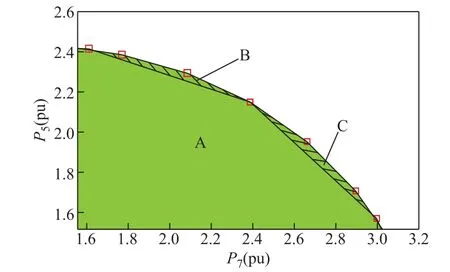
图6 不同Δθ构建的SVSRBFig.6 Constructed SVSRB compared with different Δθ

3.1.4 迭代步长的分析

本节进一步详细分析了牛拉法收敛精度ε和BICGSTAB迭代法收敛阈值εb的选取过程。

1）牛拉法收敛精度ε的选取

采用边界追踪法搜索SVSRB时，SVSRB上相邻SNB点处的系统运行信息变化较小，若牛拉法收敛精度过小，则在提高SNB点计算精度的同时，也会增加牛顿迭代次数，使得SNB点的计算耗时明显增加；而牛拉法收敛精度过大，则在减少牛顿迭代次数、提高SNB点计算效率的同时，可能无法保证SNB点的计算精度。

表5对比了牛拉法不同收敛精度对上述场景中SNB点8的计算精度和计算效率的影响。由表5可知，当牛拉法收敛精度为10-2时，直接法即可获得准确的负荷裕度，且相较于其他收敛精度，具有较少的迭代次数和较高的计算速度。

表5 不同ε下SNB点8的计算效率对比Tab.5 Computational efficiency comparisons of 8th SNB with different ε

表6进一步对比了牛拉法收敛精度ε分别为10-2和10-8时SNB点8处系统各节点的电压幅值，并以收敛精度10-8为基准，计算了各节点电压幅值相对误差。由表6可知，ε=10-2时的各节点电压幅值相对误差均低于0.05%，进一步验证了所设牛拉法收敛精度的准确性。

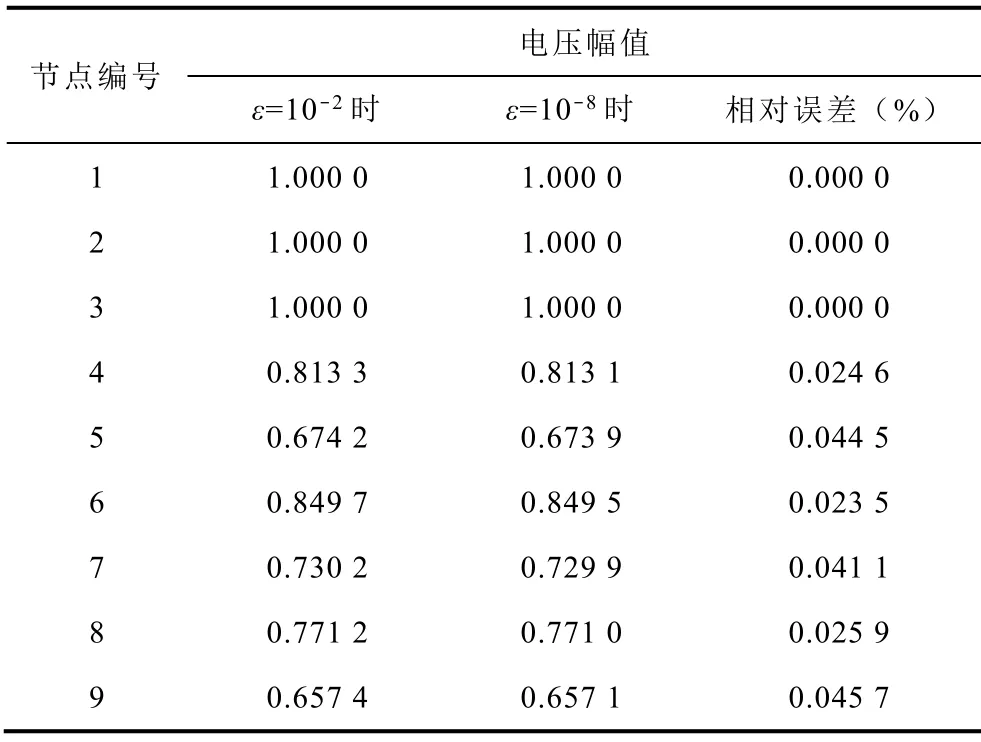
表6 不同ε下SNB点8处各节点电压幅值对比Tab.6 Comparison of voltage magnitude of 8th SNB with different ε

综上所述，本文设置的牛拉法收敛精度10-2可以很好地保证SNB点精度，且具有较高的计算效率，因此，本文中的牛拉法迭代步长选为10-2。

2）BICGSTAB迭代法收敛阈值εb的选取

BICGSTAB迭代法是以当前残差与预设阈值进行比较来判断何时停止迭代，故对阈值的修改即可实现对求解精度的控制[24]。本文中，BICGSTAB迭代法主要用于求解牛顿迭代内部的四个低维线性方程组式（4）～式（7），因此，其收敛阈值主要影响式（4）～式（7）的求解精度。然而，对式（4）～式（7）的求解并不是为了得到其精确解，而是为了使牛顿迭代可以向非线性方程组式（1）的真实解逼近，因此，BICGSTAB迭代法的收敛精度不需太高，能保证收敛即可。

通常，采用迭代求解法求解牛拉法内部的线性方程组时，迭代求解法的收敛精度应不低于牛拉法的收敛精度[31]，结合本文选取的牛拉法收敛精度，故BICGSTAB迭代法的收敛精度应不低于10-2。而将BICGSTAB迭代法的求解精度调低可以有效降低内部线性求解所需的迭代次数，提高计算效率，故本文中BICGSTAB迭代法的收敛阈值取为10-2。

3.1.5 三维SVSRB构建

本节在二维SVSRB构建的基础上，进一步借鉴文献[23]的方法，以节点5、7、9的有功注入为坐标轴，构建了如图7所示的三维SVSRB。由图7的三维SVSRB搜索结果可知：本文所提基于CPUGPU异构的静态电压稳定域边界并行计算方法在二维、三维有功注入空间均可以实现SVSRB的准确构建。

图7 WECC3机9节点系统的三维SVSRBFig.7 3-dimensional SVSRB of WECC 9 test system

进一步，借鉴文献[25]的安全域边界近似方法，对图7所示的三维SVSRB近似，结果如图8所示，相应的边界近似解析表达式详见附表1。

附表1 WECC-9节点系统的三维SVSRB近似边界解析表达式系数App.Tab.1 Analytical expressions for the 3-dimensional SVSRB approximation hyperplanes of WECC-9 test system

图8 WECC-9系统的三维SVSRB近似边界Fig.8 Approximated 3-dimensional SVSRB of WECC-9 test system

3.2 Case13659pegase测试系统

WECC3机9节点系统算例验证了所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法的准确性，本节进一步以欧洲电网13 659节点系统为例[33]，采用所提的静态电压稳定域边界并行计算方法分别构建case13659pegase系统的二维和三维SVSRB，以进一步验证所提方法构建大规模区域互联电力系统SVSRB的可行性。

分别选择节点4、5和节点4、6作为关键节点，采用本文所提的方法分别在节点4、5和4、6的二维有功注入空间构建SVSRB，结果如图9所示。进一步，以节点4、5、6的有功注入量为坐标轴构建三维SVSRB，结果如图10所示。

图9 case13659pegase系统的二维SVSRBFig.9 2-dimensional SVSRB of European 13659PEGASE test system

图9和图10结果表明：本文所提基于CPUGPU异构的静态电压稳定域边界并行计算方法可以用于高维电力系统SVSRB的构建，验证了本文所提方法的可行性。

进一步，对图9和图10所得的二维、三维SVSRB进行近似，结果如图11和图12所示。其中，图9a和图11a中，以节点4、5有功注入为坐标轴的二维SVSRB近似解析表达式为

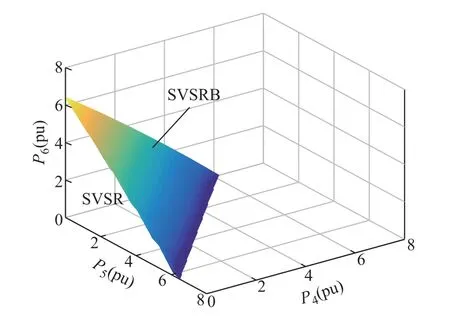
图10 case13659pegase系统的三维SVSRBFig.10 3-dimensional SVSRB of European 13659PEGASE test system

图11 case13659pegase系统的二维SVSRB近似边界Fig.11 Approximated 2-dimensional SVSRB of European 13659PEGASE test system

图12 case13659pegase系统的三维SVSRB近似边界Fig.12 Approximated 3-dimensional SVSRB of European 13659PEGASE test system

图9b和图11b中，以节点4、6有功注入为坐标轴的二维SVSRB近似解析表达式为

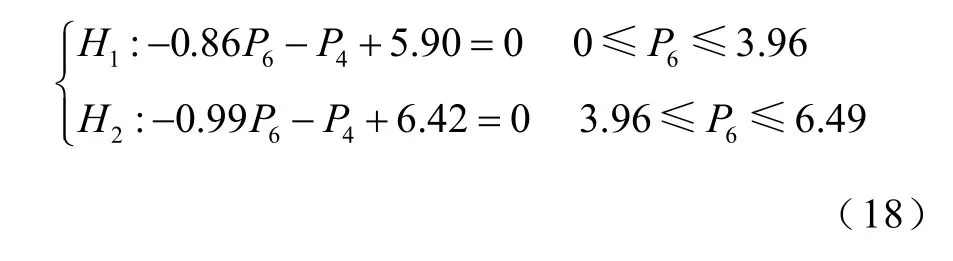
图10和图12中，以节点4、5和6有功注入为坐标轴的SVSRB近似解析表达式详见附表2。

附表2 欧洲电网13659节点系统三维SVSRB近似边界解析表达式系数App.Tab.2 Analytical expressions for the 3-dimensional SVSRB approximation hyperplanes of European 13659PEGASE test system

3.3 SVSRB并行计算效率分析

为验证所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法构建区域互联电力系统SVSRB的有效性，本节分别以case2737sop、case3120sp、case7092、case9241pegase、case11624和case13659pegase测试系统为例，对基于CPUGPU异构平台的BICGSTAB迭代法与Jacobi+ILU(0)预处理相结合的计算方法、基于CPU平台的BICGSTAB迭代法与Jacobi+ILU(0)预处理相结合的计算方法、基于CPU平台的LU分解算法以及基于射线的直接法搜索二维、三维SVSRB的计算耗时进行对比。上述四种算法搜索的二维和三维SVSRB计算耗时结果见表7和表8。

表7和表8中“—”表示测试系统的SVSRB构建失败。表中基于射线的直接法构建电力系统SVSRB失败的主要原因为：利用负荷参数二阶导数预估SNB点初值存在给定初值不稳定、不精确的现象，从而导致直接法计算部分测试系统SVSRB上的SNB点时结果不收敛。而基于CPU平台的LU分解算法构建电力系统SVSRB失败的主要原因是由于LU分解算法受功率增长方向的影响，不合理的功率增长方向会使LU分解算法求解线性方程组式（4）～式（7）出现错误解，从而导致牛顿迭代不收敛，SNB点求解失败。对比表7和表8结果可知：基于射线的直接法虽理论上可行，但实际应用时很难构建出系统的SVSRB；基于CPU平台的LU分解算法虽然可以快速搜索SVSRB，但该算法稳定性较差；而对式（4）～式（7）采用Jacobi+ILU(0)两阶段预处理的BICGSTAB迭代法与牛顿迭代法相结合的方式使得本文所提基于边界追踪的直接法对于上述测试系统无论在CPU平台还是CPU-GPU异构平台均可构建出系统完整的SVSRB，有效验证了本文所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法适用性更强、鲁棒性更高。其主要原因是：直接法对初值非常敏感，基于射线的直接法因以基态为起始点，基态与SNB点距离较远，直接法牛顿迭代时给定的初值不够合理，因而牛顿迭代时SNB点收敛较慢甚至不收敛，不能构建完整的SVSRB；而高度优化的LU分解算法可快速求解式（4）～式（7）并结合边界追踪法可实现SVSRB的高效构建，但基于CPU平台的LU分解算法对功率增长方向较为敏感，不当的功率增长方向会导致SNB点求解失败，无法构建完整的SVSRB；而本文所提并行计算方法因给定的牛顿迭代初值非常接近相邻待求解SNB点的真实值，SNB点初值精度较高，因此易获得SNB点收敛解，便于构建完整的SVSRB。

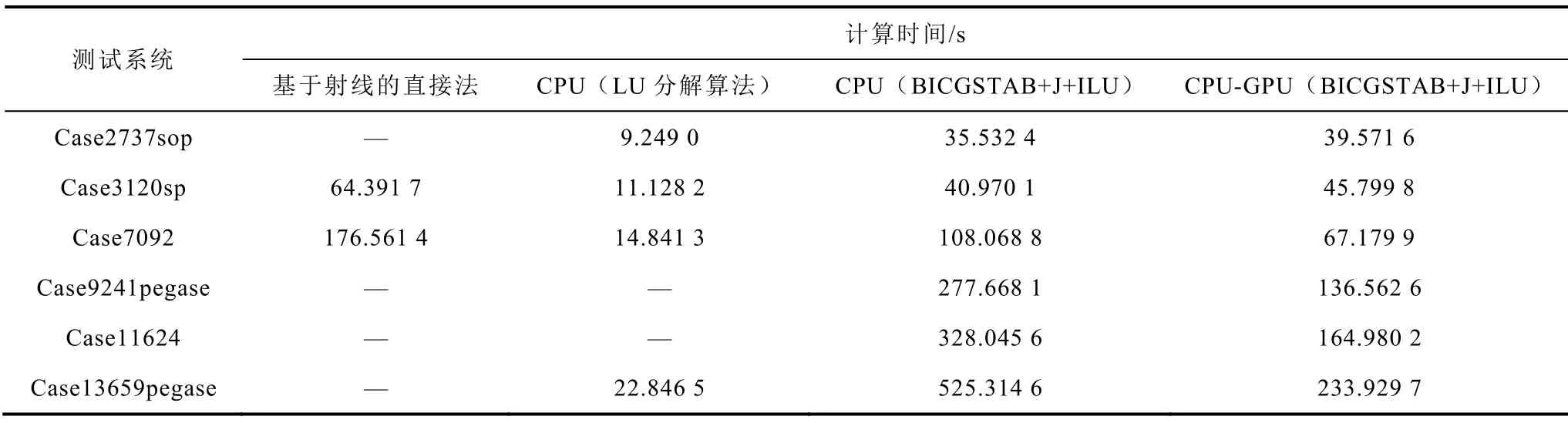
表7 不同测试系统的二维SVSRB计算时间对比Tab.7 Computational times of 2-dimensional SVSRB for different bulk power grids

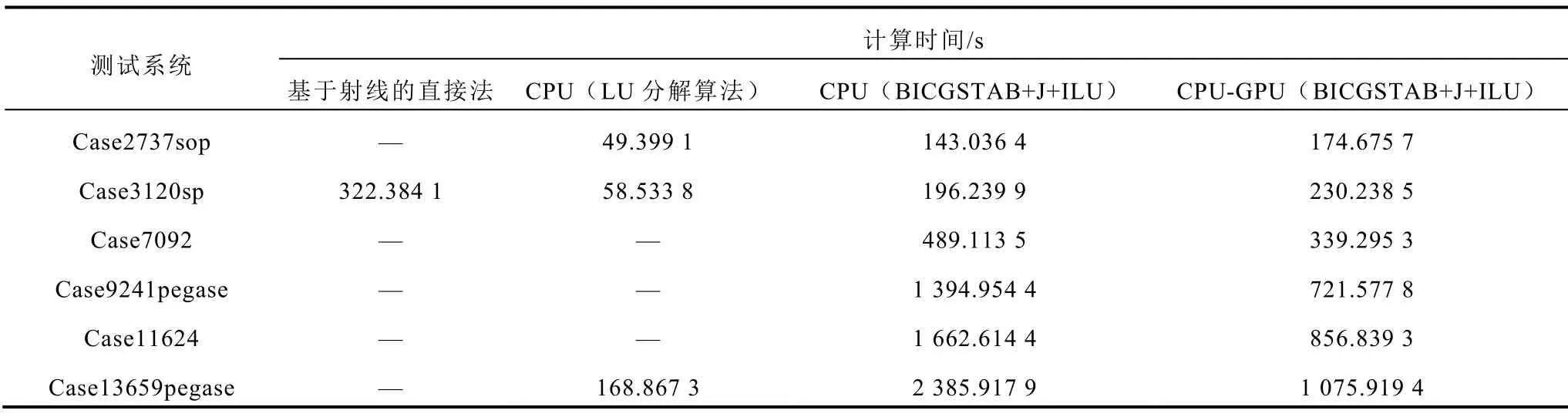
表8 不同测试系统的三维SVSRB计算时间对比Tab.8 Computational times of 3-dimensional SVSRB for different bulk power grids

进一步分析表7和表8中CPU平台和CPUGPU异构平台下采用基于边界追踪的直接法搜索SVSRB的结果表明：对于case2737sop和case3120sp测试系统，本文所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法构建SVSRB的计算耗时相较基于CPU平台的基于边界追踪的直接法更长。其主要原因是：GPU作为CPU的外部设备，二者间的数据移植比较耗时[34]，利用GPU的并行技术加速对case2737sop和case3120sp测试系统线性方程组求解的同时，CPU和GPU之间的数据传输也会耗费一定时间，且对于 case2737sop和case3120sp测试系统而言，CPU和GPU间的数据交互耗时要多于GPU并行求解带来的加速性。当测试系统规模大于case3120sp时，采用所提基于CPUGPU异构的静态电压稳定域边界并行计算方法构建SVSRB的效率优势逐渐突显，对case13659pegase测试系统的二维SVSRB，所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法构建SVSRB的加速比是在CPU平台中构建SVSRB的2.25倍。

表9以CPU平台构建SVSRB的计算耗时为基准，给出了采用所提基于CPU-GPU异构平台的SVSRB并行计算方法在搜索二维和三维SVSRB时的相对计算效率。由于采用CPU-GPU异构平台的SVSRB搜索方法在case2737sop和case3120sp系统的计算耗时大于在CPU平台中的构建耗时，因而对应的表9中的计算效率提升量记为0。表9的计算耗时对比结果表明：对于大型区域互联电力系统，采用本文所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法可进一步加快SVSRB的构建效率，降低了构建SVSRB所需的计算耗时，验证了所提方法在构建大规模区域互联电力系统静态电压稳定域中的有效性。

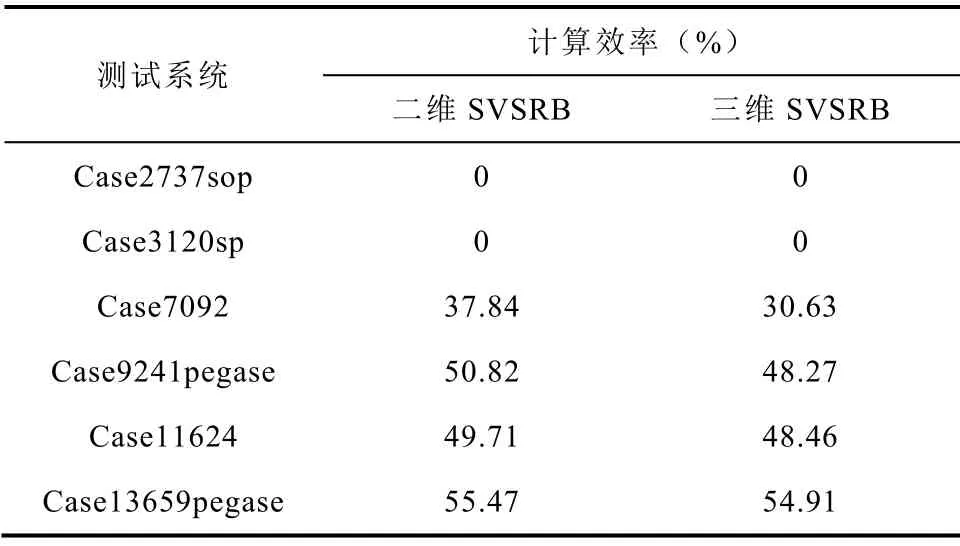
表9 不同测试系统的SVSRB并行计算效率对比Tab.9 Comparisons of computational efficiency for SVSRB in bulk power grids

上述对比结果表明：本文所提基于CPU-GPU异构的静态电压稳定域边界并行计算方法适用于区域互联电力系统SVSRB的构建，且在保证高精度的前提下具有较高的计算效率。

4 结论

本文提出一种基于CPU-GPU异构的电力系统静态电压稳定域边界并行计算方法，通过WECC3机9节点测试系统、波兰电网2737节点测试系统和3120节点测试系统、欧洲电网7092节点测试系统、9241节点测试系统、11624节点测试系统和13659节点测试系统算例对本文所提方法的准确性和有效性进行了分析验证，相关结论如下：

1）所提方法将直接法与边界追踪法相结合，成功克服了直接法初值选择的不足，且与CPU-GPU异构平台有效结合，解决了直接法计算量大、计算复杂度高的瓶颈。

2）所提方法可实现二维以及高维有功注入空间内SVSRB的准确构建,且采用CPU-GPU异构平台有效降低了SVSRB的构建耗时，提高了SVSRB的计算效率。

3）所提方法因给定初值稳定，且采用Jacobi+ILU(0)两阶段预处理的BICGSTAB迭代法求解线性方程组，具有良好的算法稳定性和适用性。

所提基于CPU-GPU异构的电力系统静态电压稳定域边界并行计算方法虽可实现由SNB点构成的SVSRB的快速构建，但对于实际电力系统，LIB点同样也可诱发系统电压失稳，因此，如何实现含SNB点和LIB点的SVSRB并行计算将是本文下一步的研究重点。

附 录

（续）