Xu Xiangjie Jiang Rui

(School of Cyber Science and Engineering, Southeast University, Nanjing 210096, China)

Abstract：To share data securely with secure attribute revocation, anti-collusion, and dynamic user management in the 5G device-to-device (D2D) environment, a novel dynamic anti-collusion ciphertext policy attribute-based encryption (NDA-CP-ABE) scheme in the 5G D2D environment is proposed. On the basis of the ciphertext policy attribute-based encryption algorithm, fine-grained access control and secure attribute revocation are realized, and the confidentiality of data is guaranteed. A polynomial function is adopted in the ciphertext generation phase to realize dynamic user management. A random number is used to prevent a collusion attack among the legitimate user equipment (UE), revoked UE, and external network attackers. Finally, on the basis of the Diffie-Hellman problem, the NDA-CP-ABE scheme is formally proved, and the simulation performances are compared with those of similar schemes. The results show that data can be securely shared through a D2D channel with secure attribute revocation, anti-collusion, and dynamic user management. Moreover, compared with similar schemes, the NDA-CP-ABE scheme has higher efficiency in encryption, decryption, and storage.

Key words：device-to-device (D2D); attribute revocation; user management; dynamic anti-collusion ciphertext policy attribute-based encryption (NDA-CP-ABE); access control

The widespread application of the 5G mobile network greatly increases the amount of user equipment (UE), which brings much overhead to 5G base stations. Device-to-device (D2D) communication is considered a promising technology that releases the pressure on 5G base stations because the UE can communicate directly with each other without being directly involved in the 5G infrastructure. In addition, D2D communication can alleviate the mobile traffic explosion problem[1]and solve the problem of a spectrum resource shortage in a wireless communication system. However, data security is difficult to guarantee.

To realize data confidentiality protection in a data-sharing system, the data access control method is widely used.However, the traditional method of access control has multiple copies of ciphertext for different users with different keys, which may cause much storage overhead. Sahai et al.[2]proposed the concept of the attribute-based encryption (ABE) algorithm, which has two types: ciphertext policy attribute-based encryption (CP-ABE)[3]and key policy attribute-based encryption (KP-ABE)[4]. CP-ABE schemes[5-9]became promising for their efficient and fine-grained data access control. However, these schemes cannot realize attribute revocation. Yang et al.[10]proposed a cloud storage system based on CP-ABE to realize efficient data access control with attribute revocation. However, the users whose attributes were revoked may threaten the security of the scheme through a collusion attack.

The schemes[11-14]could achieve attribute revocation but could not realize dynamic user management. Wei et al. proposed an attribute-based access control scheme for multi-authority cloud storage[15]by adopting the binary tree to dynamically remove the user from the system. However, this algorithm incurred more computational overhead. Han et al. proposed a CP-ABE scheme that realized the application of hidden policy and white-box traceability[16]. However, although the illegal and invalidated users could be removed from the system in this scheme when new users joined the system, the proposed algorithm would become inapplicable. Thus, this scheme could only realize partial user management.

5G access and handover security, IoT security, D2D security, V2X security, and network slice security are five aspects of security for the current 3GPP 5G network[17]. 5G D2D communication provides efficient and low-latency service for the UE and should be designed to meet security requirements, such as low computational cost, secure and effective device discovery, confidentiality and integrity protection, secure group communication, and fine-grained access control of devices. To solve the problem of data confidentiality in D2D communication, Zhang et al.[18]proposed a secure data-sharing protocol, which merged the advantages of public-key cryptography and symmetric encryption to achieve data security in D2D communication. However, the protocol could not support fine-grained data access control. Yan et al.[19]proposed a flexible data access control scheme in D2D communications to realize secure data communication among UE, but the computational cost of the scheme was high. Li et al.[20]proposed a data access control scheme with multi-authority CP-ABE encryption in D2D communication. However, the multiple authorities may waste the network resources because the distributed authorities were not suitable for the D2D communication scenario.

1 Preliminaries

1.1 Bilinear mapping

Definition1(bilinear mapping) LetG1,G2andG3be three multiplicative cyclic groups of the same prime orderp. Lete:G1×G2→G3denote a bilinear map defined with the propertiesof bilinearity, non-degeneracy, and computability[21]. In bilinearity,e(ua,vb)=e(u,v)ab, ∀u∈G1, ∀v∈G2, anda,b∈Zp, whereZpdenotes an integer group with prime orderp. In non-degeneracy, ∃u∈G1, ∃v∈G2such thate(u,v)≠I, whereIis the identity element ofG3. In computability, for any elementu∈G1,v∈G2, there is a polynomial-time algorithm to calculatee(u,v).

1.2 Decisional bilinear Diffie-Hellman problem

Definition2(DBDH problem) Letgbe a generator of groupGwith prime orderpanda,b,c,d∈Zpbe randomly chosen. Makega,gb,gc∈Gppublic. It is difficult to distinguish between (g,ga,gb,gc,e(g,g)abc) and (g,ga,gb,gc,e(g,g)d)[22].

Definition3The function Fu, which outputsz∈{0,1}, has advantageεfor solving the DBDH problem in groupG, supposing that

Pr[Fu(e(g,g)abc)=0]-Pr[Fu(e(g,g)d)=0]≥ε

1.3 Linear secret sharing scheme

Definition4(linear secret sharing scheme) A secret sharing scheme over a set of partiesPis called a linear secret sharing scheme (LSSS) if the shares for each party form a vector overZp, and there is a matrixMcalled the share-generating matrix[23]. The matrixMhasmrows andncolumns. Fori=1,2,…,l, thei-th rowMiofMis labeled asρ(i), whereρdenotes the function fromi=1,2,…,mtoP. Given a column vectorv={s,y2,…,yn}, wheres∈Zpis the secret to be shared andy2,y3,…,yn∈Zpare randomly chosen;Mvis the vector ofmshares of the secretsaccording to the scheme. The partyρ(i) obtains the shareλi=(Mv)iofsfromMv.

2 NDA-CP-ABE Scheme

2.1 System model

Fig.1 presents the system architecture of the NDA-CP-ABE scheme in the 5G D2D environment. The system includes four kinds of entities: Trusted Authority, Core Server, Cloud, and UE, whose functions and characteristics are introduced as follows.

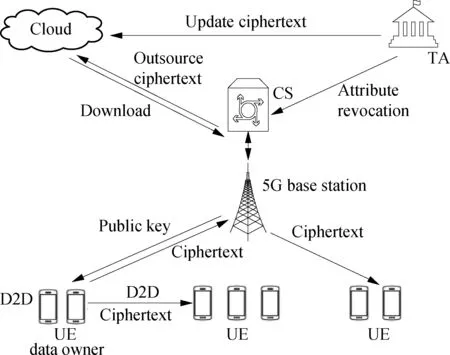
Fig.1 System architecture of the NDA-CP-ABE scheme

Trusted Authority (TA) is a trusted entity and is responsible for generating the security parameter. The TA outputs the secret keys and the corresponding update keys to the UE and performs the user management and attribute revocation process. Core Server (CS) is the core server of the 5G infrastructure and provides high-speed Internet service. The CS controls the normal operation of the base stations, which is responsible for transferring data to the other entities, including the D2D devices. The Cloud is responsible for storing the data uploaded from the UE. It also provides the ciphertext update service for attribute revocation and user management. UE communicate with each other through the D2D channel. The data owner of the UE defines the access policy and directly transmits the ciphertext (CT) to the other UE. The data owner of the UE can also outsource the ciphertext to the Cloud for further use.

2.2 Construction of the NDA-CP-ABE scheme

2.2.1 System initialization

The steps of system initialization are as follows.

1) D2D setup. The CS generates a public/private key pair (pi,si) for each UEi, wherepiis the public key andsiis the secret key for D2D discovery. Then the CS sends the key pair (pi,si) to UEithrough the secure channel.

2) Secure D2D discovery. UE1generatesR=rI1t1andT1(R), whererdenotes UE1’s request for D2D discovery;I1is UE1’s identity information;t1is the time stamp; andT1(R) is a signature ofRwiths1. The SHA256 signature algorithm is used to generate the signature for the UE. Then, UE1broadcasts the request ofRT1(R). After receiving the request from UE1, UE2checks the receivedRwith theRcomputed by verifyingT1(R). After successful verification, UE2generatesRS=r′I2t2andT2(RS), wherer′ denotes UE2’s response for discovery;t2is the time stamp;I2is UE2’s identity information; andT2(RS) is the signature ofRSwiths2. Then, UE2returnsRST2(RS) to UE1. UE1checks the receivedRSwith theRScomputed by verifyingT2(RS). After successful verification, the D2D communication channel is opened. The data owner UE1constructs the secure D2D channel and shares data with UE2, UE3,…, UEn. In the same way, the discovery procedures among UE2, UE3,…, UEncan be finished.

3) TA setup. The TA initializes the system with the TA setup algorithm: TA Setup (1λ)→(SK,PK,{Vk,Pk},τT), which inputs the security parameterλand outputsSK=(α,β),PK=(e(g,g)α,gβ).SKandPKare the secret key and public key of the TA, respectively. The TA also outputs {Vk=vk,Pk=[gvkH(γk)]β}, which are the secret version key and public key of each attributeγk, respectively.τTdenotes the minimum time difference threshold in the system.

4) UE setup. The UE sends its identity informationNto the TA, and then the TA conducts the UE Setup algorithm, UE Setup (N)→(GPKN,GSKN), to compute and return each UE’s global public key GPKN=gNand global secret key GSKN=zN.

5) Time synchronization. Each sender of the entities records the current timeτ1when every piece of information is to be sent and appendedτ1to the information. Upon receiving the information from other entities, the receiver entity should obtain the current timeτ2. If |τ1-τ2|<τT, the conversation continues. Otherwise, the receiver entity returnsτ1τ2eto the sender entity.edenotes the error code of the current conversation.

2.2.2 Secret key generation

In this subsection, the TA generates the secret keys for each UE. The detailed secret key generation step is as follows.

The TA assigns the valid UE a set of attributesSjand then generates the UE’s secret key SKj:

SKj=(Kj,Kj,k) =[Kj=g1/zj+uj/α,Kj,k=(gvkH(γk))βuj]

where ∀j∈SU,γk∈Sj,ujis randomly chosen, andSUdenotes the set of all the UE. After generating the secret keys, the TA securely sends the secret keys to the corresponding UE. The attribute setSjconsists of many attributes according to the UE’s gender, nationality, academic degree, or much other information of different levels.

2.2.3 Ciphertext generation

In this section, UEi(data owner) defines the data access policy and encrypts the data according to the corresponding attributes. The detailed encryption process is as follows.

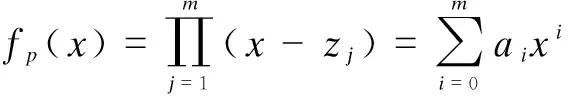
2.2.4 Data decryption

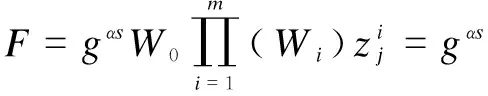
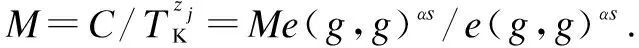
2.2.5 Attribute revocation

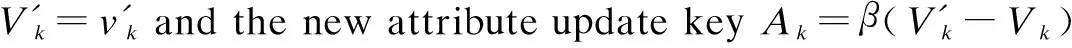
2.2.6 User management

When UEμin the UE setSUis removed from the system for certain reasons, the TA should remove it directly without updating other legitimate UE’s secret keys.

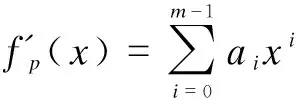
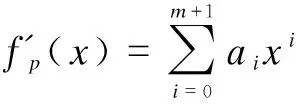
3 Formal Security Analysis

3.1 Proof of correctness

Theorem1The NDA-CP-ABE scheme is correct; that is, legitimate UE can successfully decryptCT, and can achieve safe attribute revocation and user management.

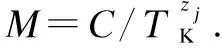
3.2 Proof of security

Theorem2The NDA-CP-ABE scheme can resist a chosen-ciphertext attack (CCA). If an adversary has an advantageεthat can be neglected in polynomial time for attacking the NDA-CP-ABE scheme with at mostqk,qc, andqdnumbers of queries in the Secret Key Generation phase, Ciphertext Generation phase, and Data Decryption phase, respectively, with maximum timet; then the challenger can solve the DBDH problem with an advantage ofPr=ε(1-qk/2n)/(qkqeqd), which can be neglected in polynomial time.

ProofSuppose that there is an adversary who has advantageεfor attacking the NDA-CP-ABE scheme.

Setup the challenger generatesSK=(α,β),PK=(e(g,g)α,gβ), which are the secret key and public key of the TA, respectively, and {Vk=vk,Pk=[gvkH(γk)]β}, which are the secret version key and public key of each attributeγk, respectively. Then, the adversary selects a set of attributesSkthat satisfy the access structure. The challenger then sends the public keys to the adversary of the attribute setSk.

Phase 1 is that the adversary selectively refers (j,Sj) inSAto the challenger to obtain the corresponding secret key SKj. The challenger then calculates the secret key as follows: SKj=[Kj=g1/zj+uj/α,Kj,k=(gvkH(γk))βuj].

The adversary refers to two messagesm0andm1of equal length but cannot decrypt the challenge message properly with the queried keys and any other keys fromSk. The challenger then randomly chooses a bit ofbin {0,1}, encrypts it under the access structure, and then sendsCTto the adversary.

Phase 2 is similar to Phase 1. The adversary refers (j,Sj) inSAto the challenger to obtain the corresponding secret key SKj. However, the secret key does not satisfy the access policy.

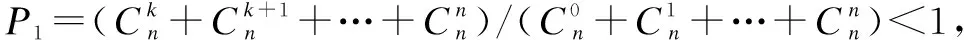
3.3 Collusion attack resistance

Theorem3NDA-CP-ABE is secure with collusion attack resistance; that is, it can prevent the collusion attack among the legitimate UE, the revoked UE, and the external attackers.

ProofFor the legitimate UE and the revoked UE, the attributek∈S1of UE1is revoked, and UE2is the legitimate UE with attribute setS2. The ciphertext is encrypted withW=S1∪S2. The key update key,Uj,k=gujAk, is associated with every UE’s identity. Therefore, UE1and UE2cannot update their secret key to the latest version and cannot decrypt the ciphertext.

For the legitimate UE and external attacker,UE3is the legitimate UE with attribute setS3, and UE4is the network attacker. The ciphertext is encrypted withW=S3∪S4, whereS4denotes the extra attribute set needed to decrypt the ciphertext for UE3. The secret key SKjis associated withuj, which is randomly chosen. Therefore, UE3and UE4cannot decrypt theCT, either collectively or individually.

For the collusion attack between the revoked UE,γ5∈S5of UE5andγ6∈S6of UE6are revoked. The ciphertext is encrypted withW=S5∪S6. The secret key SKjand update keyUj,k=gujAkare associated withuj, which is randomly chosen. Therefore, UE5and UE6cannot share the secret keys related to their attributes to decrypt the ciphertext.

3.4 Attribute revocation security

Theorem4The scheme can achieve attribute revocation security.

3.5 User management security

Theorem5The NDA-CP-ABE scheme can realize secure, dynamic, and efficient user management.

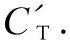
3.6 Security comparison

In this section, the security performance of NDA-CP-ABE is compared with Xue et al.’s scheme[13](Scheme 1), Wei et al.’s scheme[15](Scheme 2), Han et al.’s scheme[16](Scheme 3), Yan et al.’s scheme[19](Scheme 4), and Li et al.’s scheme[20](Scheme 5) in terms of attribute revocation, collusion attack resistance, user management, and whether these schemes support the 5G D2D environment in Tab. 1. Therein, “√” and “×” mean that the scheme can and cannot meet the corresponding security goal, respectively.

According to Tab. 1, the NDA-CP-ABE scheme can successfully realize collusion attack resistance, secure attribute revocation, and secure user management in the 5G D2D environment. However, Scheme 1 cannot realize dynamic user management and is not fit for the 5G D2D scenario; Scheme 2 cannot realize secure attribute revocation and is not fit for the 5G D2D scenario; Scheme 3 can only realize partial user management because the algorithm in Scheme 3 cannot support the new users to dynamically enter the system. In addition, Scheme 3 cannot realize attribute revocation, collusion attack resistance, and fitness for the 5G D2D scenario. Scheme 4 cannot realize attribute revocation, collusion attack resistance and dynamic user management. Scheme 5 cannot realize secure attribute revocation and dynamic user management.

Tab.1 Security Comparison

4 Performance Analysis

The performances of computational overhead and storage overhead are compared in this section by comparing the NDA-CP-ABE scheme with the schemes in Refs.[13,15-16,19-20]. The simulation is conducted on an Ubuntu 16.04 system with a 2.20 GHz processor and 4.00 GB RAM.

4.1 Computational overhead

This section compares the NDA-CP-ABE scheme for computational overhead with the schemes in Refs.[13,15-16,19-20] in terms of encryption and decryption. The computational cost of multiplicative operationcm, exponential operationce, hash functionch, and the pairing operationcpin the groupGis considered. The number of attributesnaranges from 2 to 20, and the number of UEnuin the system is 100.

4.1.1 Encryption overhead

The computational cost for encryption among six schemes is compared in Fig.2. The computational cost of the NDA-CP-ABE scheme((3ce+ch)na+cm) is smaller than that of Scheme 1 ((2ce+cm)na). Although the former has (na-1) more multiplicative calculations, the latter hasnamore hash calculations, andnamore exponential calculations. In addition, the encryption cost of the NDA-CP-ABE scheme is much less than those of Scheme 2 to Scheme 5 which are (6ce+4cm+ch)na+(ce+cm)nu, (5ce+3cm)na+3cm+3ce, (2ce+2cm)na+ce, and (5ce+2cm)na, respectively.

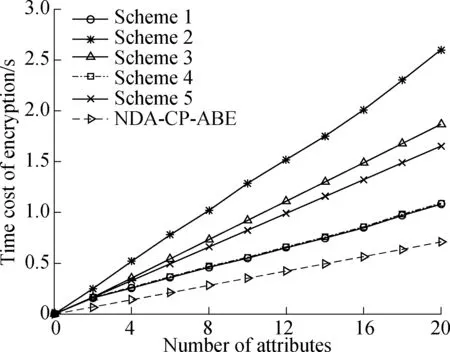
Fig.2 Comparison of encryption time

4.1.2 Decryption overhead

The computational cost for decryption among the six schemes is compared in Fig.3. The decryption cost of the NDA-CP-ABE scheme((2cp+cm+ce)na+cm+2ce) is less than that of Scheme 1 ((3cp+2cm)na+ce). Although the former has (na+1) more exponential calculations, the latter hasnamore paring calculations and (na-1) more multiplicative calculations. The computational cost of the NDA-CP-ABE scheme is much less than those of Scheme 2 and Scheme 3 which are (4cp+4cm+ce+ch)naand (3cp+2cm+ce)na+2cp+3ce+5cm. The decryption cost of the NDA-CP-ABE scheme is less than that of Scheme 4 ((2cp+3cm)na). Although the former has (na+2) more exponential calculations, the latter has (2na-1) more multiplicative calculations. The decryption cost of NDA-CP-ABE is slightly higher than that of Scheme 5 ((3cp+ce)na) because the latter hasnamore paring calculations while the former has (na+1) more multiplicative calculations and two more exponential calculations. However, Scheme 5 cannot realize secure attribute revocation and dynamic user management.

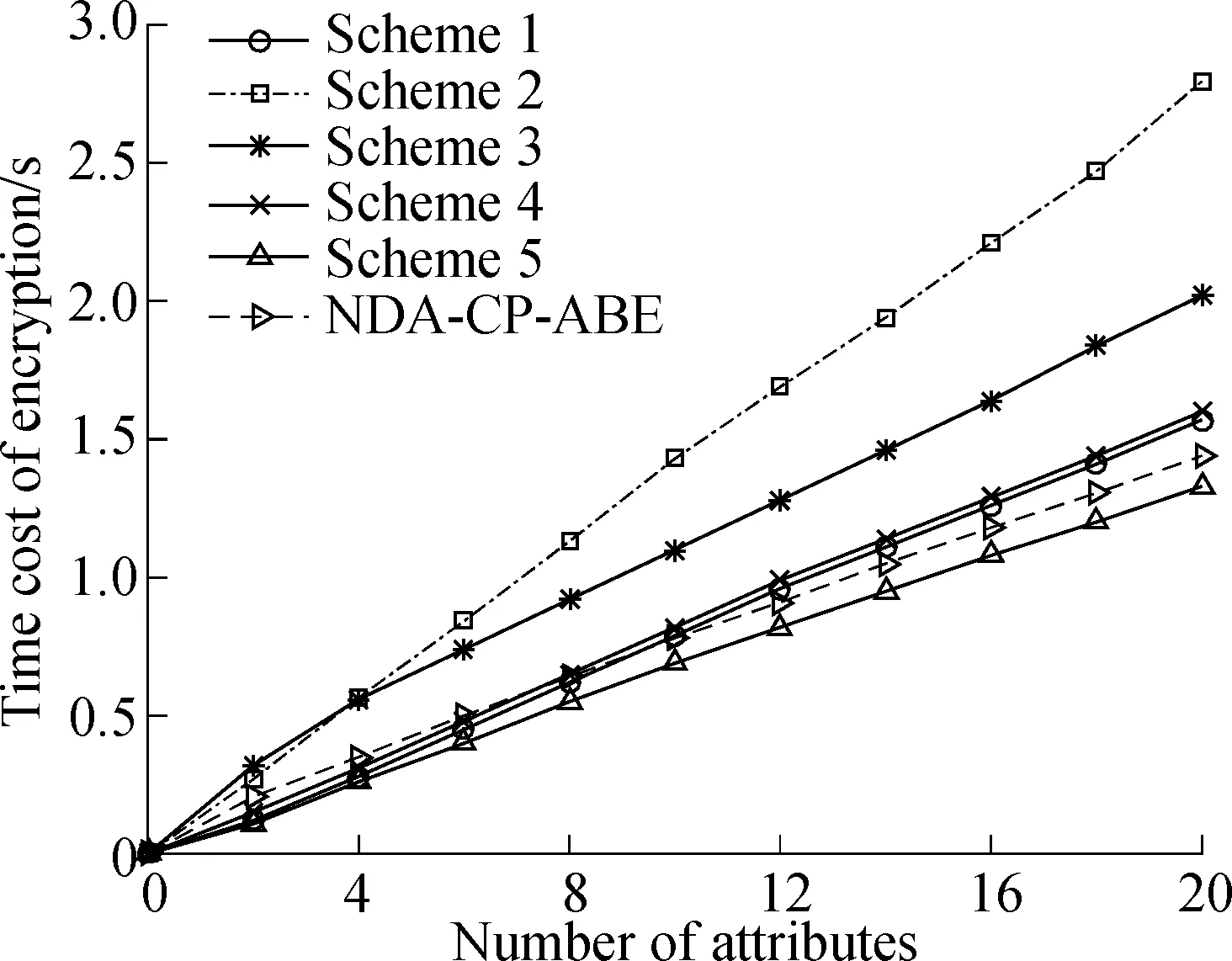
Fig.3 Comparison of decryption time

4.2 Storage overhead

In this section, the NDA-CP-ABE scheme for storage overhead of the ciphertext is compared with the schemes in Refs.[13,15-16,19-20].smdenotes the size of the plaintextM. The storage overhead of the NDA-CP-ABE scheme ((sm+2na+1)|p|) is smaller than those of Scheme 1 to Scheme 5 which are (3na+3+sm)|p|, (5na+4+sm)|p|, (3na+1+sm)|p|, (2na+sm)nj|p|, and (3na+1+sm)|p|, respectively.njdenotes the number of junctions needed in Ref.[19]. Generally speaking,nj>1.

5 Conclusions

1) The secure sharing of data in the 5G D2D environment is realized. The ciphertext policy attribute-based encryption algorithm is adopted to realize safe data sharing. Only the UE with sufficient attributes that satisfy the access policy defined by the data owner can decrypt the ciphertext.

2) Secure attribute revocation in the 5G D2D environment is realized. When the attributes of the UE are revoked, the CP-ABE algorithm only updates other related UE’s attribute keys to control the access rights. The revoked UE can no longer decrypt the ciphertext after the secure attribute revocation.

3) Dynamic and efficient user management in the 5G D2D environment is realized. The polynomial function algorithm is adopted to encrypt the data. When UE loses the permission to the data, the algorithm dynamically removes the UE from the system without updating other UE’s relating attribute keys. When new UE obtains permission to enter the system, the algorithm assigns the UE the access right to the ciphertext without updating the existing UE’s relating attribute keys.

4) The NDA-CP-ABE scheme can withstand a collusion attack among the legitimate UE, the revoked UE, and the external attackers with the secret value related to each piece of UE in the 5G D2D environment.