张铭浩，余 聪

(中山大学 物理与天文学院，广东 珠海 519082)

磁陀星是宇宙中磁场最强的一类中子星，也是目前人类发现的宇宙中磁场最强的一类天体.磁陀星外部磁层的行为由磁压所主导，等离子体压强可忽略不计，因此适用无力条件.本文从无力条件出发，通过自相似假设将Grad-Shafranov方程化为变量分离形式，从而简化计算，得到了Grad-Shafranov方程的数值解，并依此给出了不同电流参数下的磁场线投影图、三维磁场线图，并通过数值积分得到了磁场线偏转角以及磁能随电流参数的变化关系.

1 无力磁场模型

1.1 无力场的静力学条件

无力场是磁流体力学中的一个概念.当磁场的磁压强远大于等离子体压强的情况下，等离子体压强可以被忽略而只用考虑磁压强.从静力学平衡角度分析，在磁场足够强的区域中，带电粒子受到洛伦兹力的量级远大于压力梯度、重力以及惯性力的量级，从而静力学平衡关系简化为洛伦兹力为零，故该条件被称为“无力条件”.在该条件下，电流密度只有平行于磁场方向的分量.

在求解黑洞磁层、太阳日冕磁场等以磁压强为主导的很多高能天体物理问题时，无力磁场模型均能给出合理的结果.本文研究的磁陀星是中子星中具有最强磁场的一类，也是目前宇宙中已知的具有最强磁场的一类天体，因此是适用无力磁场模型的典型代表.

1.2 电流为零时磁场为有势场

由于我们研究处于稳态的磁层，高斯单位制下麦克斯韦方程组的全电流定律

退化为静磁场的安培环路定理

(1)

式(1)给出了静磁场磁感应强度与电流的关系.若电流密度J为0，可知该磁场无旋，故可写为一个标量函数(磁标势)的梯度

B=-φ

1.3 电流不为零时的磁场与Grad-Shafranov方程

1.2节中的磁标势是描述磁场的常用方法，其负梯度方向为磁场方向. 除了用磁标势φ，轴对称磁场还可以用流函数ψ(r,θ)来普遍表达：

(2)

磁标势φ的等值线为等势面，与场线处处垂直；而流函数ψ的等值线即为场线. 若电流密度J不为0，将无力条件：

代入安培环路定理(1)可以得到磁场的流函数满足如下方程[2]：

×B=α(ψ)B

(3)

由于稳态和轴对称性的要求，无力系数α是ψ的函数.

在球坐标系中，满足式(3)的微分方程用磁场流函数的形式可写为

(4)

其中I(ψ)为流经磁场线ψ的总电流强度.

由式(4)给出的磁场的绕极轴旋转的分量为

(5)

对式(4)做变量替换μ=cosθ，则式(4)化为Grad-Shafranov方程的形式：

(6)

(7)

式(7)是线性方程，可以变量分离. 不难验证单极子、偶极子、四极子等轴对称极向磁场都满足式(7).

由于磁陀星磁场足够强，可以对壳层施加足够的应力导致壳层剪切，从而使磁场扭曲. 要研究其扭曲磁场的位形，我们只能对式(6)进行求解.

2 对扭曲磁场的数值求解

2.1 自相似假设下扭曲磁场本征值问题的求解

与可变量分离的式(7)不同，式(6)是非线性方程，求解二维非线性偏微分方程非常困难. 人们采用自相似的假设，并在太阳物理、强磁星的研究中取得了和观测吻合的结果. 我们同样采用自相似假设，认为满足式(6)待求磁场的流函数可以变量分离[2]，即ψ可以写成只含有r的部分与只含有μ的部分之乘积：

ψ=R(r)F(μ)

并假设流函数关于r的部分为幂函数形式[2]：

R(r)=r-p

讨论电流强度满足流函数ψ的幂函数的形式：

(8)

其中C，p为待定参数. 则式(6)可化为变量分离的形式：

R(r)=r-p，

(9)

接下来的工作只需找到满足式(9)的解F(μ)，即可对上述假设下磁场的性质进行讨论. 我们注意到式(9)是二阶常微分方程. 一般情况下，二阶常微分方程只需要两个初始条件即可确定. 而式(9)的求解是一个本征值问题. 因此我们需要找到合适的C、p值，使得式(9)的解刚好满足给定的3个边界条件.

我们用流函数重新表述球坐标系下磁场的3个分量，并给出在实际情况下偏微分方程(6)所满足的边界条件

注意到

做变量替换μ=cosθ后可以得到磁场3个分量与r、μ的关系

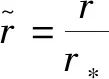
(10)

(11)

(12)

方程第一个边界条件要求在极轴上Bφ=0，即

F(1)=0

第二个边界条件要求在极轴与星体表面交点处的磁感应强度恒为B*，即

F′(1)=-2

F′(0)=0

我们采用“打靶法”解决上述本征值问题. 利用 第一、第二个边界条件，从μ=1处开始积分，找到满足第三个边界条件的解对应的C，p值. 图1给出了满足上述三个边界条件的参数C与p的关系. 可以看出在p=0.63附近，C达到最大值0.8732.

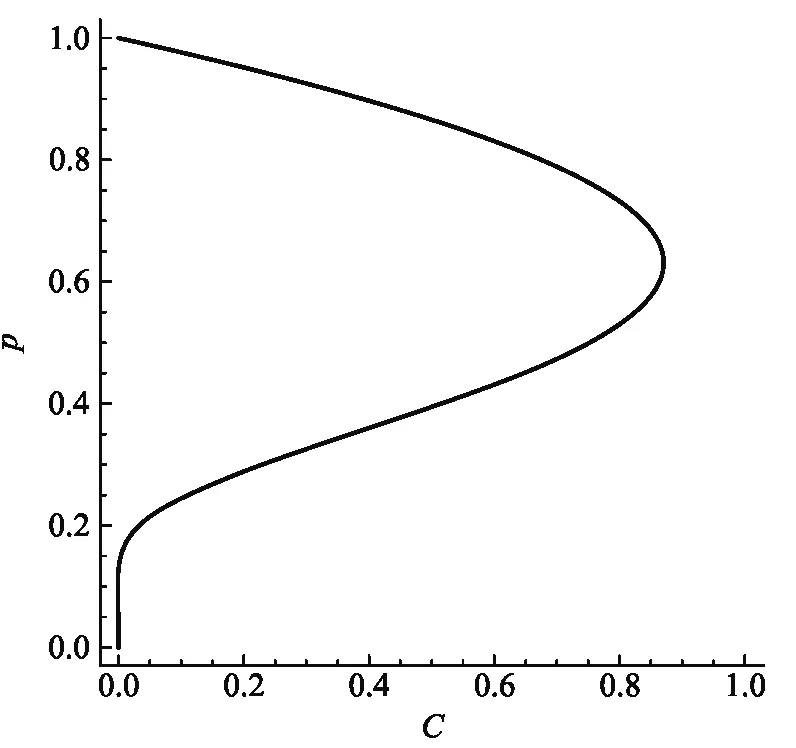
图1 满足式(8)边界条件的C与p的关系

图2给出了数值求解微分方程(8)得到的解F(μ)在不同C,p值下的函数图像.可以发现在p→0时,除了在μ=0附近，F(μ)→2(1-μ).

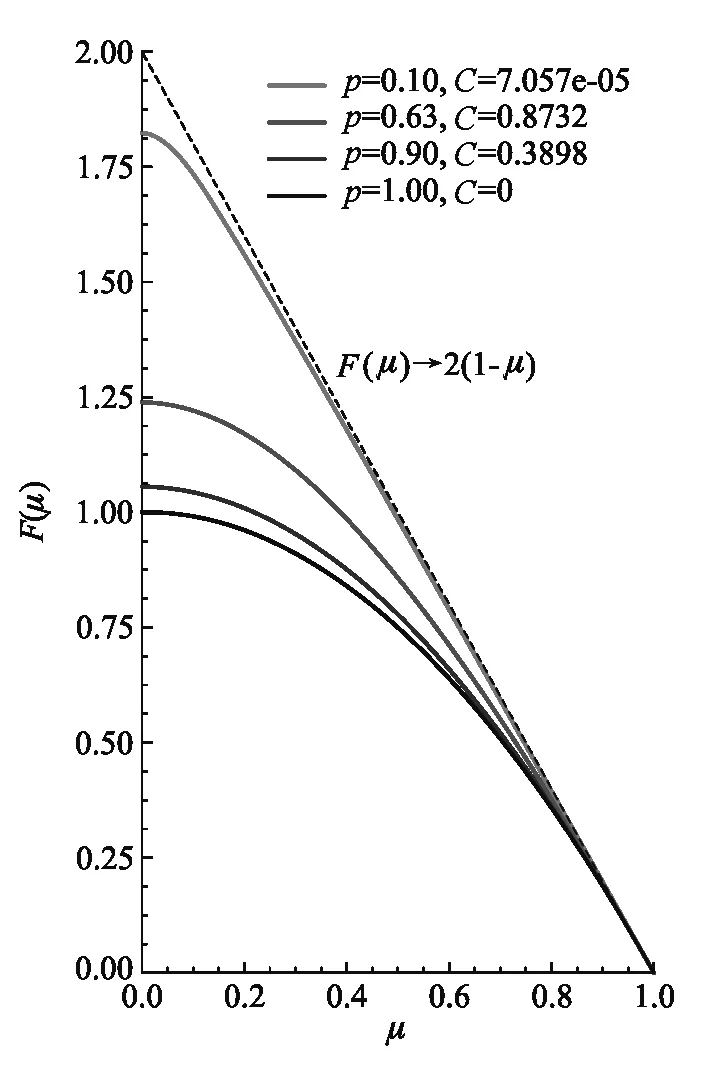
图2 不同p值下的式(8)的解F(μ)

2.2 磁场线的绘制与对上述解的讨论

图3 磁场等值线图

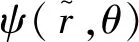
图4 磁场线在r-θ平面的投影以及扭曲情况

3 求解磁感线的偏转角

在电流参数C≠0时，根据矢量与其积分曲线的关系，我们有

从磁感线在星体表面的起始位置到终止位置对dφ积分，可得到偏转角Δφ.根据积分上下限选取的不同，我们会得到不同的偏转角

(13)

作变量替换μ=cosθ，从而积分化为

选取不同θ值作为磁感线在星体表面的起(止)位置，对上式数值积分，分别作Δφ与C，p的关系，得到图5的结果. 可以看出随p减小，在C达到最大值前，各位置起止的偏转角Δφ均随C的增大而增大；在C达到最大值后，N-S极附近起止的磁感线偏转角Δφ随C的减小而增大，赤道附近起止的磁感线偏转角Δφ随C的减小而先增后减.

图5 偏转角Δφ在不同θ值下与参数的关系

其中图5(a)、图5(b)中黑色加粗线为起止点在N-S极(θ=0)处磁场线的扭曲情况Δφ(θ=0)，即为磁场线的最大偏转角. 由图5(a)可以看出：在电流参数C取最大值0.8732时，磁场线的最大偏转角在1.8 rad附近.由图5(b)可以看出：随p值增大，N-S极磁场线的偏转角趋于π,该结果与文献[2]给出的结果一致.

作Δφ-θ图，得到在不同电流参数下，偏转角与磁感线在星体表面起止点位置θ的关系，如图6所示.可以看出在同一电流参数下，越靠近两级的磁场线偏转角度越大，这说明磁场线在两极处的扭曲比赤道附近更明显，该结论与图4给出的结果是一致的.

图6 偏转角Δφ与磁感线起点位置的θ值的关系

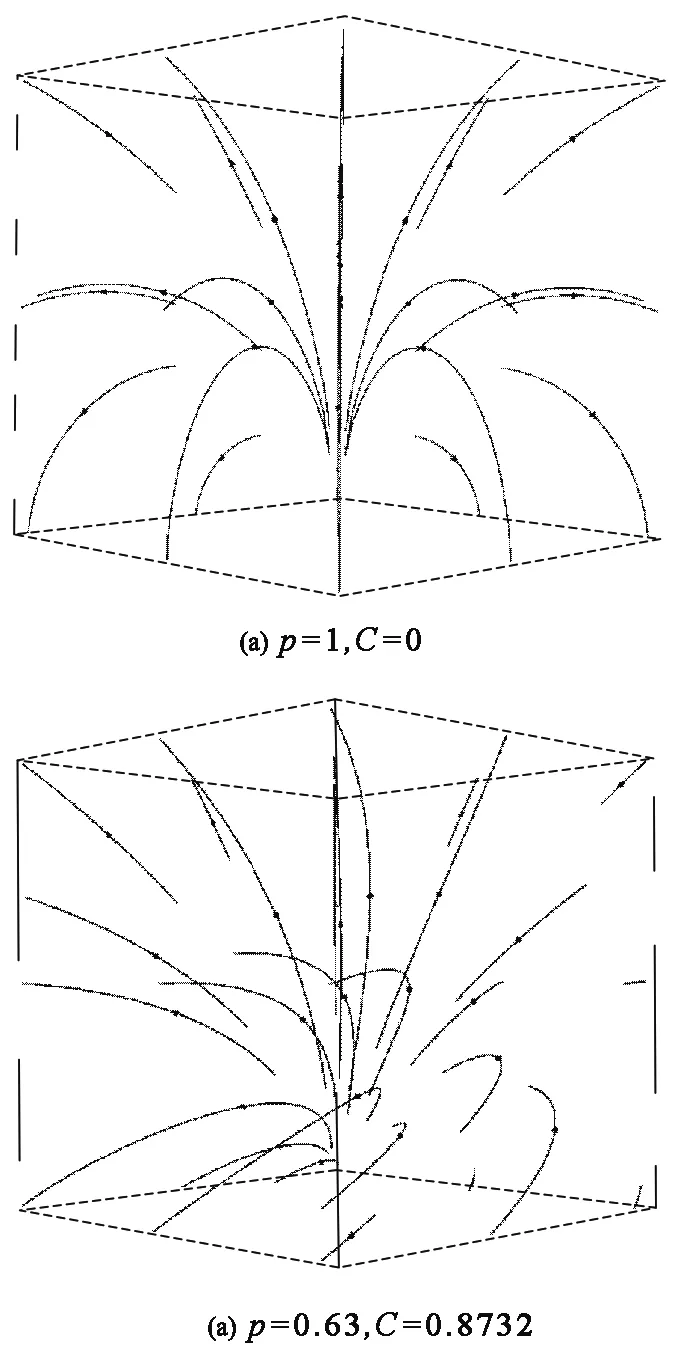
图7 三维磁场线

4 计算磁陀星磁能随磁场扭曲的变化关系

在高斯单位制下，对磁场能量密度在除星体外的全空间进行积分，可得到磁陀星磁场能量E：

(14)

写为分量形式：

由于我们讨论的解可以变量分离，上述积分可以化为以下形式：

取不同的C、p值，对以上3式进行数值积分并求和，可得到磁陀星磁场能量随参数C以及起止点N-S极的磁感线偏转角度ΔφN-S的关系. 取偶极子情况的磁场能量Edipole为1，根据积分结果绘图，磁场能量与偏转角ΔφN-S的关系如图8(a)所示；磁场能量与电流参数C的关系如图8(b)所示. 由图可知磁陀星磁能随磁场N-S极偏转角增大而增大.

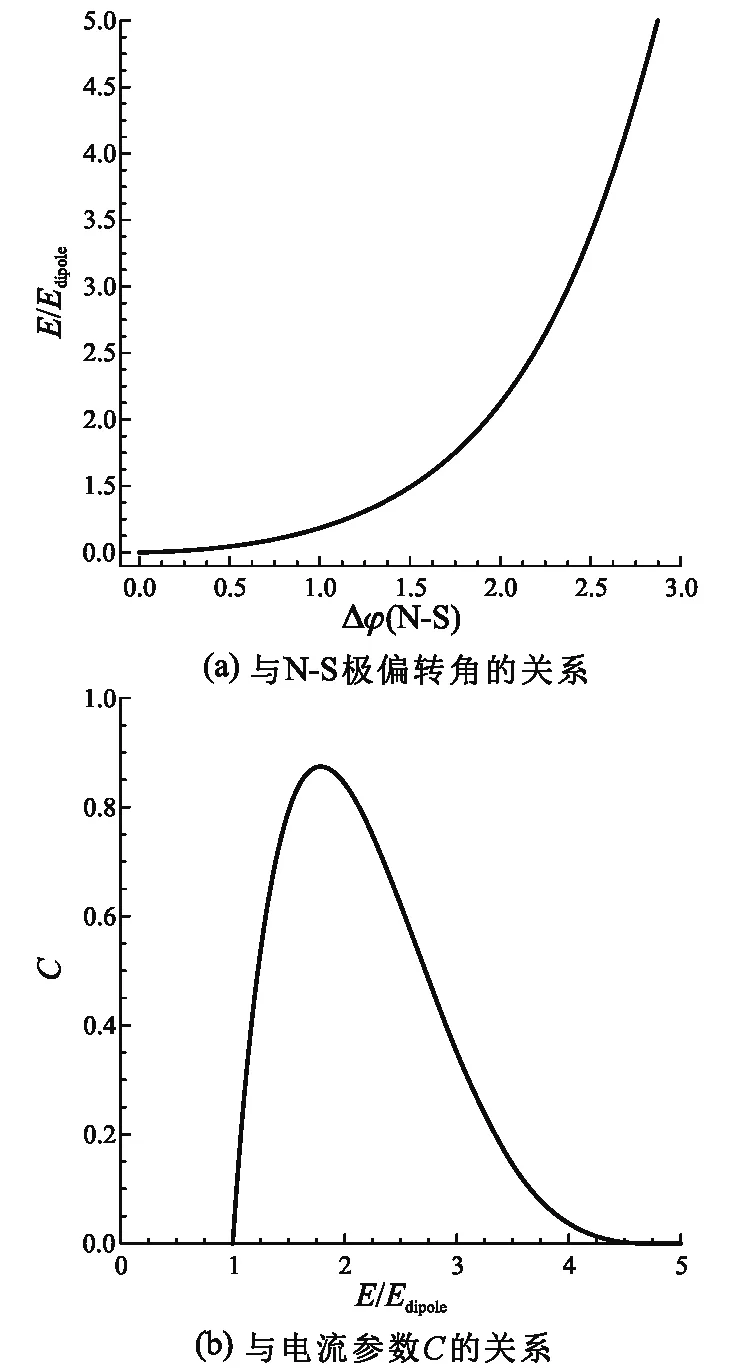
图8 磁陀星磁能的变化关系

5 总结

Grad-Shafranov方程的变量分离解能够给出在一定近似条件下的磁陀星附近磁场的性质.本文首先从无力条件出发，在自相似假设下数值求解了变量分离的Grad-Shafranov方程，得到了磁场的流函数解，并由该解绘制了磁感线、磁感线偏转程度随电流参数的关系.随后通过数值计算得到了偏转角，并探讨了偏转角与磁感线起止位置、电流参数的关系，得到两极附近起止的磁感线偏转角度大于赤道的结论，给出了磁感线的三维模拟图.以上结果与其他文献中基本一致.最后通过对磁场能量密度积分计算磁能，通过数值计算给出了在本文假设下的星体磁能随偏转角以及电流参数的变化关系，得到磁能随N-S极偏转角增大而增大的结论.

本文虽以自相似假设出发，但得到的结果依然 能够反映出磁陀星磁场的一些关键性质.基于本文的计算可以对磁陀星的磁场演化做进一步的研究.