■黄信璋

集合是高中数学的重要概念,是研究数学问题的基础和工具。集合是每年高考的必考内容,高考主要考查两个方面:一是集合本身的知识,二是集合语言与其他数学知识的综合运用。高考对常用逻辑用语的考查主要涉及四种命题的关系、全称量词与存在量词的关系、命题的否定等。下面举例分析集合与常用逻辑用语的常见典型考题,供大家学习与提高。

一、集合的含义

判断元素能否构成集合,关键是集合中元素的确定性,即能否找到一个明确的评判标准来衡量元素是否为集合中的元素,若标准明确则可以构成集合,否则不可以构成集合。当一个集合中的元素含字母时,可利用集合中元素的确定性求出集合中字母的所有取值,再利用集合元素的互异性进行检验。两个集合相等,元素必须相同。解决集合问题,要注意集合元素的“三性”,即确定性,互异性和无序性。

例1(多选题)已知集合A中的元素满足x=3k-1,k∈Z,则下列表示正确的是( )。

A.-2∈AB.-11∉A

C.3k2-1∈AD.-34∉A

解:令3k-1=-2,解得k=-,而,可知-2∉A。令3k-1=-11,解得k=-∉Z,所以-11∉A。由k2∈Z,可得3k2-1∈A。令3k-1=-34,解得k=-11,而-11∈Z,所以-34∈A。应选B,C。

跟踪训练1:已知x,y都是非零实数,可能的取值组成的集合为A,则下列判断正确的是( )。

A.3∈A,-1∉AB.3∈A,-1∈A

C.3∉A,-1∈AD.3∉A,-1∉A

提示:当x>0,y>0时,z=1+1+1=3;当x>0,y<0时,z=1-1-1=-1;当x<0,y>0时,z=-1+1-1=-1;当x<0,y<0时,z=-1-1+1=-1。据此可得集合A={-1,3}。故3∈A,-1∈A。应选B。

二、集合的表示

用列举法表示集合应注意两点:(1)弄清集合中的元素是什么,是数,是点,还是其他元素;(2)集合中的元素一定要写全,但不能重复。用描述法表示集合,应弄清集合的属性,是数集,点集,还是其他类型的集合。一般地,数集用一个字母代表其元素,而点集则用一个有序实数对来代表其元素。当集合的元素个数很少,容易写出全部元素时,常用列举法表示集合;当集合的元素个数较多,不容易写出全部元素时,常用描述法表示集合。对一些元素有规律的无限集,也可用列举法表示,如正奇数集可写为{1,3,5,7,9,…}。

例2(多选题)下列各组中M,P表示不同集合的是( )。

A.M={3,-1},P={(3,-1)}

B.M={(3,1)},P={(1,3)}

C.M={y|y=x2+1,x∈R},P={x|x=t2+1,t∈R}

D.M={y|y=x2-1,x∈R},P={(x,y)|y=x2-1,x∈R}

解:A 中,M是由3,-1 两个元素构成的集合,而集合P是由点(3,-1)构成的集合。B中,(3,1)与(1,3)表示不同的点,故M≠P。D 中,M是二次函数y=x2-1,x∈R 的所有因变量组成的集合,而集合P是二次函数y=x2-1,x∈R 图像上所有点组成的集合。应选A,B,D。

跟踪训练2:用列举法写出集合=____。

提示:由,x∈Z,可得3-x为3的因数,所以3-x=±1或3-x=±3,所以=±1,所以-3,-1,1,3满足题意。答案为{-3,-1,1,3}。

三、集合间的基本关系

空集是任何集合的子集,在涉及集合关系时,必须优先考虑空集的情况,否则会造成漏解;已知两个集合间的关系求参数时,关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系。常用数轴、Venn图来直观解决这类问题。

例3下列各组中的两个集合之间存在包含关系的是( )。

①集合P={x|x=2n+1,n∈Z},Q={x|x=2(n-1),n∈Z};②集合P={x|x=2n-1,n∈N+},Q={x|x=2n+1,n∈N+};③集合P={x|x2-x=0},Q={x|x=,n∈Z}。

A.①②③ B.①③

C.②③ D.①②

解:①中,对于Q,由n∈Z,可得n-1∈Z,因此Q表示偶数集,P表示奇数集,所以P∩Q=∅。②中,P是由1,3,5,…所有正奇数组成的集合,Q是由3,5,7,…所有大于1的正奇数组成的集合,且1∉Q,所以集合P⊇Q。③中,P={0,1},对于Q,当n为奇数时,x==1,当n为偶数时x==0,即Q={0,1},所以P=Q。应选C。

跟踪训练3:用Venn图表示下列集合之间的关系:A={x|x是平行四边形},B={x|x是矩形},C={x|x是正方形},D={x|x是菱形}。

提示:根据几何图形的相关知识,明确各元素所在集合之间的关系,可用Venn 图表示A,B,C,D之间的关系,如图1所示。

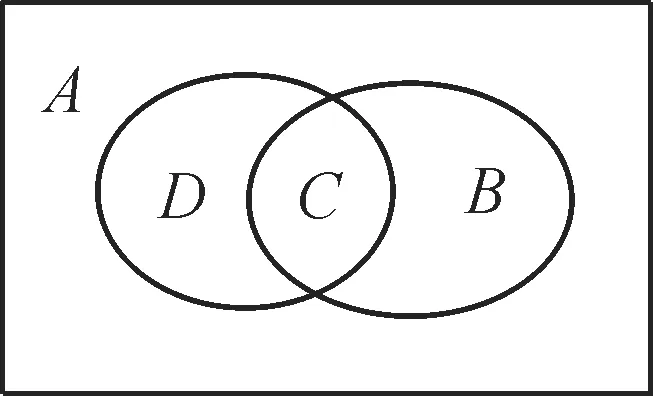
图1

四、并集与交集

求并集应注意的两点:注意元素的互异性这一属性,重复的元素只能取一个;对于元素个数无限的集合求并集时,可利用数轴分析求解,但要注意端点的值能否取到。求交集应注意的两点:若集合的代表元素是方程的根,则应求出方程的根后,再求两集合的交集;若集合的代表元素是有序数对,则交集是指方程组的解集,其解集是点集。

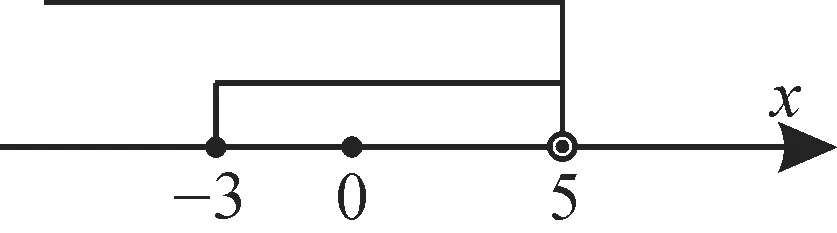
例4已知集合M={x|-2

解:由M∪N=M,可得N⊆M。当N=∅,即2t+1≤2-t,t≤时,M∪N=M成立;当N≠∅时,利用数轴可得不等式组

综上可知,实数t的取值范围是{t|t≤2}。

跟踪训练4:设集合A={x|x2-2x=0},B={x|x2-2ax+a2-a=0}。

(1)若A∩B=B,求a的取值范围。

(2)若A∪B=B,求a的值。

提示:(1)由x2-2x=0,可得x=0 或x=2,所以集合A={0,2}。

由A∩B=B,可得B⊆A,则B=∅或B={0}或B={2}或B={0,2}。当B=∅时,由Δ=4a2-4(a2-a)=4a<0,可得a<0;当B={0}时,由可得a=0;当B={2}时,由此时无解;当B={0,2}时,由解得a=1。综上可知,实数a的取值范围是{a|a=1 或a≤0}。

(2)由A∪B=B,可得A⊆B。由于A={0,2},而B中方程至多有两个根,所以A=B。由(1)知a=1。

五、补集及综合应用

补集是相对于全集而言的,一方面,若没有定义全集,则不存在补集的说法;另一方面,补集的元素逃不出全集的范围。补集既是集合之间的一种关系,也是集合之间的一种运算。在给定全集U的情况下,求集合A的补集的前提是A为全集U的子集,随着所选全集的不同,得到的补集也是不同的。求集合的补集的三种方法:定义法,当集合中的元素较少时,可利用定义直接求解;Venn 图法,借助Venn 图可直观地求出补集;数轴法,当集合中的元素连续且无限时,可借助数轴求补集,此时需注意端点值的取舍。

例5已知全集为U,集合A={1,3,5,7},∁UA={2,4,6},∁UB={1,4,6},则集合B=_____。

解:由A={1,3,5,7},∁UA={2,4,6},可得U={1,2,3,4,5,6,7}。因为∁UB={1,4,6},所以B={2,3,5,7}。

跟踪训练5:已知全集U={x|x≤5},集合A={x|-3≤x<5},则∁UA=_____。

提示:将全集U和集合A分别表示在数轴上,如图2所示。

图2

由补集的定义可知,∁UA={x|x<-3或x=5}。

六、与集合有关的创新问题

以集合为背景的创新问题是高考命题的一个热点,这类题目常以问题为核心,考查探究、发现的能力,常见的命题形式有新定义、新运算等。解决新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决。对于这类选择题,可结合选项通过验证,用排除、对比、特值等方法求解。

例6已知集合A={x∈N|x2-2x-3≤0},B={1,3},定义集合A,B之间的运算“*”:A*B={x|x=x1+x2,x1∈A,x2∈B},则A*B中的所有元素之和为( )。

A.15 B.16

C.20 D.21

解:由x2-2x-3≤0,x∈N,可得-1≤x≤3,x∈N,所以集合A={0,1,2,3}。因为A*B={x|x=x1+x2,x1∈A,x2∈B},所以A*B中的元素为0+1=1,0+3=3,1+1=2,1+3=4,2+1=3(舍去),2+3=5,3+1=4(舍去),3+3=6,所以A*B={1,2,3,4,5,6},所以A*B中的所有元素之和为21。应选D。

跟踪训练6:若集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)是集合A的同一种分拆。若集合A有3 个元素,则集合A的不同分拆种数是_____。

提示:依据集合A的一种分拆的意义,设集合A={1,2,3},一一列举确定分拆的种数。①当A1=∅时,此时只有1 种分拆。②当A1是单元素集时,共有6种分拆,即{1}与{2,3},{1}与{1,2,3},{2}与{1,3},{2}与{1,2,3},{3}与{1,2},{3}与{1,2,3}。③当A1是双元素集时,共有12 种分拆,即{1,2}与{3},{1,3},{2,3},{1,2,3};{1,3}与{2},{1,2},{2,3},{1,2,3};{2,3}与{1},{1,2},{1,3},{1,2,3}。④当A1=A={1,2,3}时,则A2=∅,{1},{2},{3},{1,2}{1,3},{2,3},{1,2,3},共8种分拆。综上可知,共有分拆的种数为27。

七、充分条件与必要条件问题

充分、必要、充要条件判断的两种方法:(1)定义法,若p⇒q,q⇒/p,则p是q的充分不必要条件;若p⇒/q,q⇒p,则p是q的必要不充分条件;若p⇒q,q⇒p,则p是q的充要条件;若p⇒/q,q⇒/p,则p是q的既不充分也不必要条件。(2)集合法,对于集合A={x|x满足条件p},B={x|x满足条件q},若A⊆B,则p是q的充分条件;若A⊇B,则p是q的必要条件;若A=B,则p是q的充要条件;若AB,则p是q的充分不必要条件;若AB,则p是q的必要不充分条件。p是q的充要条件意味着“p成立,则q一定成立;p不成立,则q一定不成立”。要判断p是q的充要条件,需要进行两次判断:一是看p能否推出q,二是看q能否推出p,若p能推出q,q也能推出p,就可以说p是q的充要条件,否则,就不能说p是q的充要条件。

例7设a,b是实数,则“a+b>0”是“ab>0”的( )。

A.充分不必要条件

B.必要不充分条件

C.充分必要条件

D.既不充分也不必要条件

解:若a+b>0,取a=3,b=-2,则ab>0不成立;反之,若ab>0,取a=-2,b=-3,则a+b>0也不成立。因此“a+b>0”是“ab>0”的既不充分也不必要条件。应选D。

跟踪训练7:下列各题中,p是q的什么条件? (指充分不必要、必要不充分、充要、既不充分也不必要条件)

(1)p:x=1或x=2,q:x-1=。

(2)p:四边形是正方形,q:四边形的对角线互相垂直平分。

(3)p:xy>0,q:x>0,y>0。

(4)p:四边形的对角线相等,q:四边形是平行四边形。

提示:(1)x=1 或x=2⇒x-1==1 或x=2,所以p是q的充要条件。

(2)若一个四边形是正方形,则它的对角线互相垂直平分,即p⇒q;反之,若四边形的对角线互相垂直平分,则四边形不一定是正方形,即q⇒/p。因此p是q的充分不必要条件。

(3)当xy>0时,可知x>0,y>0或x<0,y<0,即p⇒/q,但q⇒p,所以p是q的必要不充分条件。

(4)因为四边形的对角线相等⇒/ 四边形是平行四边形,四边形是平行四边形⇒/ 四边形的对角线相等,因此p是q的既不充分也不必要条件。

八、根据充分、必要条件求参数取值范围

解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后列出关于参数的不等式(组)求解。求解参数的取值范围时,一定要注意区间端点值的检验,尤其是利用两个集合之间的关系求参数的取值范围,不等式是否能够取等号决定端点值的取舍,处理不当容易出现漏解或增解的现象。

例8已知p:≤2,q:x2-2x+1-m2≤0(m>0),且﹁p是﹁q的必要不充分条件,则实数m的取值范围为_____。

解:由x2-2x+1-m2≤0(m>0),可得1-m≤x≤1+m,所以q对应的集合为M={x|1-m≤x≤1+m,m>0},﹁q对应的集合为A={x|x>1+m或x<1-m,m>0}。由≤2,可得-2≤x≤10,所以p对应的集合为N={x|-2≤x≤10},﹁p对应的集合为B={x|x>10或x<-2}。因为﹁p是﹁q的必要不充分条件,所以AB,所以解得m≥9。故实数m的取值范围为[9,+∞)。

跟踪训练8:已知p:x≤1+m,q:|x-4|≤6。若p是q的必要不充分条件,则m的取值范围是( )。

A.(-∞,-1] B.(-∞,9]

C.[-1,9] D.[9,+∞)

提示:由|x-4|≤6,可得-2≤x≤10。因为p是q的必要不充分条件,所以[-2,10](-∞,1+m],所以m+1≥10,解得m≥9。应选D。

九、全称量词命题与存在量词命题

全称量词命题就是陈述某集合中所有元素都具有某种性质的命题,常见的全称量词有“一切”“每一个”“任给”等。存在量词命题就是陈述某集合中存在一个或部分元素具有某种性质的命题,常见的存在量词有“有些”“某一个”“有的”等。要否定全称量词命题“∀x∈M,p(x)”,只需在M中找到一个x,使得p(x)不成立,也就是命题“∃x∈M,﹁p(x)”成立。要否定存在量词命题“∃x∈M,p(x)”,需要验证对M中的每一个x,均有p(x)不成立,也就是命题“∀x∈M,﹁p(x)”成立。

例9下列命题中是全称量词命题并且是真命题的是( )。

A.∀x∈R,2x+1>0

B.若2x为偶数,则∀x∈N

C.所有菱形的四条边都相等

D.π是无理数

解:对于A,是全称量词命题,但不是真命题,A 不正确。对于B,是假命题,不是全称量词命题,B不正确。对于C,是全称量词命题,也是真命题,C正确。对于D,是真命题,但不是全称量词命题,D不正确。应选C。

跟踪训练9:下列是存在量词命题且是真命题的是( )。

A.∀x∈R,x2>0

B.∃x∈Z,x2>2

C.∀x∈N,x2∈N

D.∃x,y∈R,x2+y2<0

提示:对于A,∀x∈R,x2>0 是全称量词命题,不合题意。对于B,∃x∈Z,x2>2是存在量词命题,且是真命题。对于C,∀x∈N,x2∈N 是全称量词命题,不合题意。对于D,∃x,y∈R,x2+y2<0 是存在量词命题,是假命题。应选B。

十、根据复合命题的真假求参数

这类问题的求解策略:根据题目条件,推出每个命题的真假(有时不一定只有一种情况);求出每个命题是真命题时参数的取值范围;根据给出的复合命题的真假推出每个命题的真假情况,从而求出参数的取值范围。

例10 已知命题“∀x∈R,ax2+4x+1>0”是假命题,则实数a的取值范围是( )。

A.(4,+∞) B.(0,4]

C.(-∞,4] D.[0,4)

解:当原命题为真命题时,由a>0 且Δ=16-4a<0,可得a>4。故当原命题为假命题时,可得a≤4。应选C。

跟踪训练10:已知命题“∃x∈R,4x2+(a-2)x+≤0”是假命题,则实数a的取值范围为( )。

A.(-∞,0) B.[0,4]

C.[4,+∞) D.(0,4)

提示:因为命题“∃x∈R,4x2+(a-2)x+≤0”是假命题,所以其否定为“∀x∈R,4x2+(a-2)x+>0”是真命题。由此可得Δ=(a-2)2-4×4×=a2-4a<0,解得0

感悟与提高

1.已知集合A={x|x≥3},B={x|1≤x≤7},C={x|x≥a-1}。

(1)求A∩B,A∪B。

(2)若C∪A=A,求实数a的取值范围。

提示:(1)因为A={x|x≥3},B={x|1≤x≤7},所以A∩B={x|3≤x≤7},A∪B={x|x≥1}。

(2)因为C∪A=A,A={x|x≥3},C={x|x≥a-1},所以C⊆A,所以a-1≥3,可得a≥4,即实数a∈[4,+∞)。

2.设命题p:∃n∈N,n2>2n,则﹁p为( )。

A.∀n∈N,n2>2nB.∃n∈N,n2≤2n

C.∀n∈N,n2≤2nD.∃n∈N,n2=2n

提示:命题p是特称命题,故﹁p是全称命题。又“>”的否定是“≤”,因此﹁p为“∀n∈N,n2≤2n”。应选C。

3.命题“∀x∈R,∃n∈N*,使得n≥x2”的否定形式是( )。

A.∀x∈R,∃n∈N*,使得n

B.∀x∈R,∀n∈N*,使得n

C.∃x∈R,∃n∈N*,使得n

D.∃x∈R,∀n∈N*,使得n

提示:根据含有量词的命题的否定的概念,可知选D。