冯晓东，杨伟家，李 锋，赵颖超，冷新中

(1.绍兴文理学院 土木工程学院，浙江 绍兴 312000；2.绍兴市城投建筑工业化制造有限公司，浙江 绍兴 312000； 3.浙江交工集团股份有限公司，浙江 杭州 310000；4.浙江省建工集团有限责任公司，浙江 杭州 310000)

张拉整体结构是一种由连续的拉索与离散的压杆组合而成的空间索杆张力结构，构件内力以轴力的形式存在，可高效利用结构材料的拉压性能.也正因这种简单的受力形式和高效的材料利用率，使该结构的设计思想被应用于索穹顶结构[1].此外，张拉整体结构具有可折叠性，在产生大变形位移时只产生微小应变，因此在机器人[2]、航天航空[3]及生物学领域[4]都得以广泛应用.

初始预应力为张拉整体结构提供刚度，使其处于一种自平衡状态，这一过程通常称之为找形.在现有找形方法中往往以节点坐标、拓扑连接或初始预应力为变量，并根据变量的不同划分为拓扑找形和预应力找形.找形策略上则大多采用优化算法、动力松弛法、数值迭代法等求解手段获取张拉整体结构的初始形态.在拓扑找形研究中，Gan[5]利用遗传算法寻找非对称的张拉整体结构.谢胜达[6]基于小生境遗传算法对环形张拉整体结构进行拓扑优化.Yin[7]采用直接加杆和递归加杆方式来构造简单多边形张拉整体结构.在预应力找形研究中，早期由陈志华[8]提出张拉整体结构的力密度法，可有效解决带有索元的柔性空间结构初始形态确定问题.Estrada[9]基于力密度法以最小弹性势能为目标函数，采用矩阵相互迭代的方式求解结构的初始力密度.Tran[10-12]结合力密度矩阵的特征值分解和平衡矩阵的奇异值分解，提出了一系列求解张拉整体结构初始形态的方法.尚仁杰[13]则通过几何作图的方式求解张拉整体结构的初始预应力大小.Wang[14]提出一种找形计算框架，无需考虑自应力模态就能处理满足秩亏条件的力密度矩阵.K. Koohestani[15]提出一种基于LU分解的数值计算找形方法.

综上所述，张拉整体结构在找形方面的研究已较为成熟，构形简单的张拉整体结构可快速求解其初始形态，但在求解形态复杂的张拉整体结构的问题上，现有的方法在求解能力上略显不足.因此，本文将基于力密度法和矩阵分析理论，根据结构对称性，对构件分组归类，通过二次奇异值分解的方式求解张拉整体结构的初始力密度，为复杂张拉整体结构的初始形态确定提供一条新的途径.同时本文还提出一种新型张拉整体结构构形，采用不同分组计算该结构的初始状态，并制作实际模型以验证该结构的合理性，丰富了现有张拉整体结构形态的分析理论与应用实践.

1 找形算法

1.1 基本假定

本文中张拉整体结构找形计算遵循以下基本假定：

(1)各单元连接方式为铰接；

(2)不考虑自重及外部荷载；

(3)不考虑压杆屈曲以及材料非线性；

(4)不考虑结构的局部或整体失稳.

1.2 力密度法

对于任意张拉整体结构已知有n个自由节点、nf个固定节点、b个单元.根据拓扑连接关系可知其关联矩阵为Cb×n，假定连接单元k两端节点为i和j，则关联矩阵可如下表述：

(1)

定义Q=diag(q)，其中,q为构件力密度，根据单元的受力情况可建立平衡方程：

(2)

式中，Q为力密度矩阵；X,Y,Z(Xf,Yf,Zf)为结构中自有节点(固定节点)在x,y,z方向上的节点坐标矩阵；Cf为固定节点的关联矩阵.

由于张拉整体结构为自平衡结构，节点均为自由节点，因此式(2)可转化为

CTQCX=0CTQCY=0CTQCZ=0

(3)

再将上式简化为

(4)

式中，A为平衡矩阵.

结构的自应力模态数s和独立位移模态数m可根据平衡矩阵A求得：

s=b-rA

(5)

m=dn-rA

(6)

1.3 矩阵分析理论

对平衡矩阵A进行奇异值分解得

A=UVWT

(7)

U=[u1u2Ludn]

(8)

W=[w1w2Lwb]

(9)

其中U,W为正交矩阵，V为由矩阵A的非负奇异值组成的对角矩阵.且此时的自应力模态可分为两种情况[16]：

(1)自应力模态数为1(-b-rA)

在这种情况下，正交矩阵W可表示为

(10)

其中n1为力密度系数向量，满足线性齐次方程(4).

(2)自应力模态数大于1(=b-rA)

在多自应力模态状态下，正交矩阵可表示为

(11)

此时，可行自应力可由向量基的线性组合表示为：

q=α1n1+α2n2+…+αsns

(12)

在平衡矩阵A的计算过程中并不考虑结构材料特性，经奇异值分解得到的多组向量基可通过不同的线性组合，将存在无数种可行自应力结果，但并非必定满足结构拉压构件关系.为解决此问题，则需事先考虑结构的拉压关系，同时结合几何对称性，将构件划分为数个组别.

定义h为分组数量，则力密度矩阵可表示为

(13)

上式可简化为

(14)

(15)

将式(12)代入式(14)得

(16)

(17)

(18)

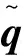
因此，式(16)可以写成

(19)

此时，线性齐次方程的所有解则取决于A的零空间矩阵维数[17].

(20)

(21)

(22)

(23)

在该情况下，式(19)无解，则说明几何对称性组别划分不合理，即该张拉整体结构在这种几何对称性下并不处于自平衡状态.为了得到可行解，需要增加组别划分数量以此增大秩亏值直到以下两种情况的出现.

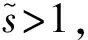
定义χ=[χ1,χ2,…,χh]，表示h组可行自应力模态向量基系数.分组后的自应力计算如下式表示：

(24)

(25)

2 稳定性判断

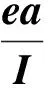
(26)

L=diag(I)

(27)

E=CTdiag(q)C

(28)

式中，I为单元长度的矢量表达；e为单元杨氏模量的矢量表达；a为单元横截面积的矢量表达；I3为三维单位矩阵；E为力密度矩阵；⊗为张量积.

若结构稳定，则KT正定.所以对于任意一个无穷小位移D，矩阵KT的二次型是正定的.

DTKTD>0

(29)

(30)

由于KE和KE处于非满秩状态，且零空间包含刚体位移，因此需忽略前6个刚体位移情况，通过最小特征值λ1反映结构的刚度强弱情况.

3 算例

本文提出一种基于立方多面体结构的新型张拉整体结构.该结构共有12个节点，每个节点均连接6根构件，共有12根压杆(红色)和24根拉索(蓝色)，结构拓扑连接方式如图1，具体节点坐标如表1.通过式(4)、(5)可得到该结构的自应力模态数为6，属于多自应力模态结构，因此其初始力密度存在多种可能.采用本文所提出的找形算法求解该张拉整体结构的初始力密度，需事先根据结构的几何对称性对构件进行分组.分组情况的不同可能会导致初始力密度的找形结果不同.

图1 新型张拉整体结构模型Fig.1 The new tensegrity structure model

表1 节点的坐标Tab.1 The nodal coordinates of the structure

3.1 几何对称找形分析

在上述初始力密度作用下，可根据式(26)考虑该结构的稳定性，其中切向刚度矩阵特征值如表3所示，从表中可以看出最小特征值为正值，则说明结构处于稳定状态.

表2 张拉整体结构初始力密度(h=5)Tab.2 Initial force density of the tensegrity structure(h=5)

表3 12杆张拉整体结构切线刚度矩阵特征值(h=5)Tab.3 Eigenvalues of the tangent stiffness matrix of the 12-strut tensegrity structure(h=5)

图2 空间12杆张拉整体结构单元分组情况(h=5)Fig.2 Elemental grouping of the 12-strut spatial tensegrity structure(h=5)

对比两种分组结果，由于分组的不同，最终得到的力密度值也会随之改变，从表5中可以看出h=5情况下结构的切线刚度矩阵最小特征值仍为正值，因此可以保证在该力密度作用下结构仍处于稳定状态，同时对比表3，在均满足结构稳定的条件下，12组分组(h=12)情况下结构所形成的刚度要略优于5组分组(h=5)的结构.

通过内点法优化(图6)，可以看出力密度标准差处于波动下降，在经过60次迭代后趋于稳定，同时一阶最优值在前15次迭代时已趋于0.最终得到的初始力密度值计算设计误差为k=8.892 0e-14，具体力密度数值如表6所示.

表5 空间12杆张拉整体结构切线刚度矩阵特征值(h=12)Tab.5 Eigenvalues of the tangent stiffness matrix of the 12-struts tensegrity structure in space(h=12)

图4 空间12杆张拉整体结构分组情况(h=12)Fig.4 Elemental grouping of the 12-strut spatial tensegrity structure(h=12)

图5 空间12杆张拉整体结构(h=36)Fig.5 The 12-strut spatial tensegrity structure(h=36)

图6 目标函数的迭代过程(h=36)Fig.6 Convergence process of the target function(h=36)

表6 张拉整体结构初始力密度(h=36)Tab.6 Initial force density of the tensegrity structure(h=36)

同时需对结构进行稳定性计算，求解得到切线刚度最小特征值为20.4484大于0，则说明结构稳定，具体数据如表7.单根构件各为一组的情况同样符合非对称结构的分组求解方式.因此，本文算法也可适用于非对称结构的初始力密度求解.

表7 空间12杆张拉整体结构切线刚度矩阵特征值(h=36)

4 张拉整体结构模型制作

由于张拉整体结构仍处于理论计算阶段，因此仍需制作模型对本文所提出的新型张拉整体结构加以验证.在模型制作过程中采用3 mm直径圆柱木棒为压杆，1 mm直径弹力绳为拉索.在模型制作完成后，尝试改变弹力绳拉伸长度，用于模拟拉索上不同初始力密度的施加状态，从而进一步说明在不同初始力密度状态下，该张拉整体结构的稳定状态.

4.1 模型制作

(31)

(32)

联立两个方程可得：

(33)

由于理论模型中最终索单元长度均一致，所以li=lj，且设置初始第1组索长为10.0 cm，最终索长为15.0 cm，根据式(33)，可求解出第2组初始索长为12.5 cm.而后对结构计算模型进行力学模型简化，完成初始模型制作，具体流程如下：

(1)裁剪16段长度为12.0±2 cm的弹力绳和8段10.0±2 cm的弹力绳，其中2 cm为预留长度，用于拉伸后的长度调节或节点绑扎固定，同时需保证拉伸后弹力绳长度均可达到15.0 cm.再根据计算得到的最终构件长度比例，还需裁剪4段长度为21.2 cm的木棒和8段长度为26.0 cm的木棒，以及12段3 cm塑料胶管，作为节点连接套筒，具体如图7所示，其中忽略木棒受压时的长度变化；

(2)可先制作4组由1根21.2 cm的木棒与2根26.0 cm的木棒用塑胶套筒连接形成的三角构件；

(3)根据理论模型的拓扑连接形式，利用弹力绳将4个三角构件连接成形.其中，索杆节点采用绑扎的方式进行固定，同时剪掉多余部分；

(4)当所有单元都已按照理论模型连接后，需测量各个拉索长度是否达到预设长度.若未达到，则需解开绑扎节点，重新调整弹力绳长度，而后重新绑扎，直至所有拉伸后的弹力绳长度达到预设长度，最终模型如图8所示.

当按照不同分组结果制作模型时，可根据式(33)，事先假定一组构件初始长度，通过改变弹力绳的初始长度，进而改变各单元的力密度值.

图7 材料准备Fig.7 Material preparation

图8 空间十二杆张拉整体结构实体模型Fig.8 Entity model of the 12-strut spatial tensegrity structure

5 结论

(1)本文的找形方法对几何对称张拉整体结构具有高效的求解能力，同时也适用于指定拉压构件的几何非对称张拉整体结构的初始力密度找形.

(2)本文算法将空间十二杆张拉整体结构构件分别划分为5组，12组以及36组，以力密度标准差为目标函数，均可求解出最优初始力密度，证实了该算法可有效求解几何对称张拉整体结构的初始力密度.

(3)基于找形结果，利用弹力线模拟拉索，木棒模拟压杆，制作空间十二杆张拉整体结构，验证了本文算法的有效性及合理性.