含模糊不确定性的汽车盘式制动器稳定性研究

2021-09-13黄晓婷李沛航

重庆理工大学学报(自然科学) 2021年8期

黄晓婷，李沛航，吕辉

(1.华南理工大学广州学院汽车与交通工程学院，广州 510800；2.华南理工大学机械与汽车工程学院，广州 510641)

汽车制动噪声已成为城市的主要噪声污染源之一。如果汽车的制动器在工作过程中处于不稳定状态，就可能引起强烈的振动，并形成刺耳的噪声。其中，频率为1～16 kHz的制动尖叫声最影响乘客的听觉，严重影响汽车的乘坐舒适性[1]。

针对汽车制动噪声，已有不少学者通过对制动器的复特征值进行分析来判断系统的稳定性，从而预测制动噪声的产生倾向[2-4]。顾华锋等[5]对重型汽车盘式制动器系统开展了缩比试验及有限元数值分析，研究了系统中主要参数对制动噪声的影响。Guan Dihua等[6]基于摩擦闭环耦合有限元模型求解了制动器复特征值的正实部，通过分析系统参数对正实部的影响，提出了抑制制动噪声的工程措施。Fritz G等[7]运用复特征值分析方法，研究了阻尼对制动噪声形成的影响。Liu P、Junior M T[8-9]分别对制动器有限元耦合模型进行了复模态分析，研究了系统参数对系统稳定性的影响，从而甄别影响制动噪声产生的主要因素。Dai Y等[10]以制动块为主要研究对象，分析了制动块结构参数对系统不稳定模态分布的影响，从抑制制动噪声的角度为制动块的设计提供了指导。吕辉等[11]将有限元法、响应面法和优化技术相结合，提出了一种降低制动器系统不稳定系数的优化方法。

上述研究均以有限元复特征值分析作为基本的数值分析方法，同时又都基于传统的确定性分析技术而开展。而基于不确定性分析的制动噪声研究工作还比较少见，Sarrouy E等[12]基于多项式混沌展开研究了随机不确定性参数对盘式制动器稳定性的影响；吕辉等[13]采用证据理论模型描述系统参数，从可能性角度对盘式制动器的稳定性进行了探索；张立军、张立军、Lü H等[14-15]将随机或区间分析与优化技术相结合，从稳健性设计角度对制动尖叫倾向性进行了优化。

由于汽车制动器结构的复杂性和工作环境的不确定性，现有方法还难以完全消除或准确预测制动噪声。实际工程运用中，制动器在摩擦接触、材料和几何属性参数等方面，广泛存在着各种不确定性。除了随机、区间不确定性情形，制动器还可能存在模糊不确定性。模糊理论在Zadeh[16]提出的模糊集合的基础上发展起来。目前，基于模糊理论的制动噪声研究尚不多见。此外，在一定条件下模糊分析模型可以向随机或区间分析模型进行转化。因此，研究模糊模型下的制动器稳定性具有更广泛的工程意义。

本文将模糊理论引入到含不确定性参数的汽车盘式制动器稳定性研究中，采用模糊变量对制动器的摩擦因数、材料和几何属性参数进行描述；将有限元复特征值分析与响应面法相结合，建立制动器稳定性分析的参数化模型；基于模糊分析算法对制动器的稳定性进行分析。方法将进一步丰富和完善不确定性条件下汽车盘式制动器稳定性的研究体系。

1 模糊理论

1.1 模糊集和隶属函数

设在论域U上有子集A⊂U，若对任一u∈U有函数μA(u)∈[0，1]，则称A为U上的模糊集，μA(u)为A的隶属函数。

若u∈U，有μA(u)=1，则u∈A是确定的。

若u∈U，有μA(u)=0，则u∉A是确定的。

若u∈U，有μA(u)∈(0，1)，则u与A间的隶属关系是不确定的，由隶属函数值μA(u)的大小即隶属度的大小而定。

若A为普通集，定义其隶属函数为CA(u)，其中A⊂U，u∈U，则：

(1)

1.2 模糊变量的截集和L-R定义

设A为论域U上的模糊集，λ∈[0，1]，记：

Aλ={u|u∈U，μA(u)≥λ}

(2)

则称Aλ为模糊集A的一个λ截集。模糊集通常可采用一个模糊变量描述。

通常，用L或R表示一个函数，当且仅当满足下列条件时：

1)L(x)=L(-x)，R(x)=R(-x)；

2)L(0)=1，R(0)=1；

3)L(x)在[0，+∞)上不增。

(3)

(4)

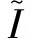
Iλ=[m+α(λ-1)，m-β(λ-1)]

(5)

特别地，当λ=0时，有：

Iλ=0=[m-α，m+β]

(6)

2 盘式制动器的稳定性分析

以某汽车盘式制动器为研究对象，完整的制动器模型通常比较复杂，包含制动盘、制动块(摩擦材料+支撑背板)、保持架、导向销和活塞等部件。为了降低分析计算量，同时又能反映系统的主要振动特性，对制动器模型进行了适当的简化处理，其简化模型如图1所示。

图1 汽车盘式制动器简化模型示意图

系统制动过程中引入了摩擦力，系统振动方程可表示为[9]：

(7)

式中：M、C、K分别为无摩擦制动器系统的质量、阻尼和刚度矩阵；X为系统振动位移矢量；Kf为摩擦接触刚度矩阵。

由式(7)可知，引入摩擦力后系统的刚度矩阵为(K-Kf)。该刚度矩阵不对称，会导致某些情形下系统的特征值和特征向量为复数，即系统的模态频率和振型为复数形式[9]。

式(7)的特征方程为：

det(s2M+sC+K-Kf)=0

(8)

式中：s为系统复特征值。

第i阶复特征值可以表示为：

si=σi+jωi

(9)

式中：σi和ωi分别为复特征值的实部和虚部。特征值实部σi可用来判断制动器系统是否处于稳定状态。当σi<0时，系统稳定；当σi>0时，系统不稳定，对应的复模态为不稳定模态。

定义第i阶复特征值的阻尼比为[8]：

(10)

式中ζi为阻尼比，可作为衡量系统稳定性的指标。从式(10)可知，当ζi为负时(即σi>0)，系统不稳定。此时，可等效认为系统存在负阻尼，即阻尼不耗散能量，反而向系统中馈入能量，引发自激振动。

3 模糊不确定性分析

在传统的制动器稳定性研究中，往往先假设某设计参数变化，而其他参数不变，分析系统稳定性的变化[8-9]。这种方法既耗时，又没有考虑参数间的交互作用，具有一定的局限性。响应面是一种构建近似模型的方法[11]。用响应面近似模拟设计变量和响应的映射关系，能够避免对复杂有限元模型的重复调用，减少运算次数，提高效率。

3.1 响应面模型

在制动器稳定性有限元分析中，系统的模态与系统参数的关系是一种典型的隐式函数关系。以系统不稳定模态为研究对象构建其2阶响应面模型[11]。与第k阶不稳定模态对应的复特征值实部和虚部的2阶多项式可表示为：

(11)

(12)

式中：σk(x)和ωk(x)分别为复特征值的实部和虚部；a0、b0、ai、bi、aii、bii、aij和bij为未知系数，可以通过试验设计和最小二乘法求解；xi(i=1，2，…，n) 为系统参数，n为参数个数。

得到响应面模型后，需检验其拟合精度，具体分析过程可参见文献[15]。

3.2 模糊不确定性分析

由于制动器工作环境和部件属性复杂多变，所以制动噪声的产生具有很大的不确定性。由于模糊不确定性可以向随机或区间不确定性转换，因此本文基于模糊模型对制动器系统的不确定性进行研究。

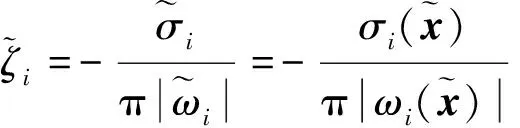
(13)

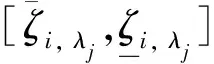
3.3 研究步骤

结合上述分析，含模糊不确定性的制动器系统稳定性研究可按如下步骤实施：

1) 选取制动器系统的研究参数，定义系统研究变量和取值空间；

2) 建立制动器系统的有限元模型，利用复特征分析技术求解系统复模态；

3) 在变量取值空间进行试验设计，结合有限元分析建立不稳定模态的响应面模型；

4) 引入模糊变量处理系统的模糊特性，基于模糊算法求解系统不稳定模态的模糊响应，并评估不确定性系统的稳定性；

5) 研究不确定性参数对系统稳定性的影响，提出改善系统稳定性的设计措施。

4 含模糊不确定性的系统稳定性研究

4.1 盘式制动器参数化模型

以图1所示的汽车盘式制动器模型为研究对象。其中，制动盘材料为灰铸铁并具有很好的耐磨性，摩擦材料由各向异性的有机材料组成，支撑背板为钢材。该制动器的有限元模型如图2所示，本文采用ABAQUS软件进行仿真分析。

图2 制动器有限元模型示意图

图3表示了该有限元模型的边界条件定义。其中制动盘被完全约束在5个螺纹孔的中心；摩擦材料与支撑背板牢固地粘在一起，制动压力均匀地加载在背板与液压活塞缸对应的接触位置，并假设加载在2个背板上的制动压力大小相等；支撑背板只能沿垂直于盘面的方向移动，而制动盘的旋转运动采用ABAQUS的MOTION卡片进行施加。

图3 有限元模型的边界条件定义示意图

对于该制动器，摩擦材料由有机各向异性材料制成，定义材料属性需要很多参数。参考文献[9]，本文将其假设为各向同性材料，但弹性模量处理为不确定变量。由于本文是基于不确定性分析而开展的研究，故该假设在一定程度上是合理的。

在有限元分析中，影响系统模态分析结果的主要参数有边界条件、材料和几何属性参数等，参考文献[8-9]，选取表1所示的系统参数进行研究。

表1 系统参数名义值和取值范围

表1中所有参数的名义值均为取值范围的中间值。除摩擦因数f和摩擦材料弹性模量E2外，其他参数取值变化范围均为名义值的10%。由于摩擦因数f的不确定性比较大，所以本文根据实际情况将其取值范围取为[0.300，0.400]；而本文对摩擦材料作了各向同性化假设，故将E2的不确定性也取得相对大一些，取值变化范围为名义值的20%。

由表1中参数的取值范围构成试验设计空间，然后采用拉丁超立方抽样方法获取90组样本点并代入到制动器有限元模型中，分析计算0～16 kHz的复模态。分析结果显示，系统的不稳定模态(具有负阻尼比)主要分布在1.9 kHz附近，虽然在其他频率上也出现了不稳定模态，但是对应的负阻尼比的绝对值都比1.9 kHz附近的小。为了更直观地显示分析结果，图4给出了随机选取的11组样本点对应的复模态阻尼比的分析结果。

图4 部分样本对应的系统复模态分布图

图4中同组样本的分析结果用相同的符号表示。从图中可明显地看出系统的不稳定模态主要集中分布在1.9 kHz附近。

基于上述分析结果，选取1.9 kHz附近的不稳定模态作为首要不稳定模态进行分析研究，构建其2阶多项式响应面模型的近似表达式：

σ(x)=σ(f，p，E1，E2，E3，ρ1，ρ2，ρ3，h1)=

-1 220.37-913.42f+2.64p-2.05E1+

18.59E2+6.16E3-10.88ρ1-175.47ρ2-

120.22ρ3+475.64h1+494.04fp-2.81fE1+

10.00fE2+2.61fE3+130.87fρ1+23.47fρ2-

80.18fρ3+122.95fh1+0.95pE1+31.70pE2-

0.06pE3-18.48pρ1-72.13pρ2+146.08pρ3-

162.65ph1-0.19E1E2+0.03E1E3+0.61E1ρ1+

0.38E1ρ2-0.58E1ρ3+0.80E1h1+2.05e-3E2E3-

2.41E2ρ1-3.93E2ρ2+0.96E2ρ3+0.72E2h1-

0.44E3ρ1-0.21E3ρ2+0.45E3ρ3-0.83E3h1+

23.81ρ1ρ2+16.52ρ1ρ3-28.32ρ1h1-11.03ρ2ρ3-

34.23ρ2h1+13.98ρ3h1-633.44f2-195.43p2-

(14)

ω(x)=ω(f，p，E1，E2，E3，ρ1，ρ2，ρ3，h1)=

1 973.88-20.39f+13.29p+15.46E1+

1.74E2-0.13E3-244.90ρ1-34.71ρ2-

7.00ρ3-5.34h1+22.08fp+0.07fE1-

0.06fE2+0.02fE3+0.61fρ1-0.30fρ2+

1.31fρ3-1.77fh1-0.04pE1-0.71pE2+

0.14pE3-2.68pρ1-3.15pρ2-1.84pρ3+

2.93ph1+0.01E1E2+3.23e-4E1E3-0.45E1ρ1-

0.06E1ρ2-0.04E1ρ3-0.08E1h1+2.57e-3E2E3-

0.39E2ρ1+5.22e-3E2ρ2+0.12E2ρ3+0.22E2h1-

0.01E3ρ1+1.84e-3E3ρ2+4.57e-3E3ρ3+

0.02E3h1+1.72ρ1ρ2+1.27ρ1ρ3+0.93ρ1h1+

0.19ρ2ρ3+0.52ρ2h1-1.06ρ3h1-4.14f2-

(15)

式中：σ(x)和ω(x)分别为1.9 kHz附近的不稳定模态对应的复特值实部和虚部。对上述响应面模型进行拟合精度检验，可知该响应面模型拟合精度高，能够用于后续分析研究[15]。

4.2 模糊不确定性下制动器的稳定性分析

各模糊变量用三元组表示，其取值如表2所示。

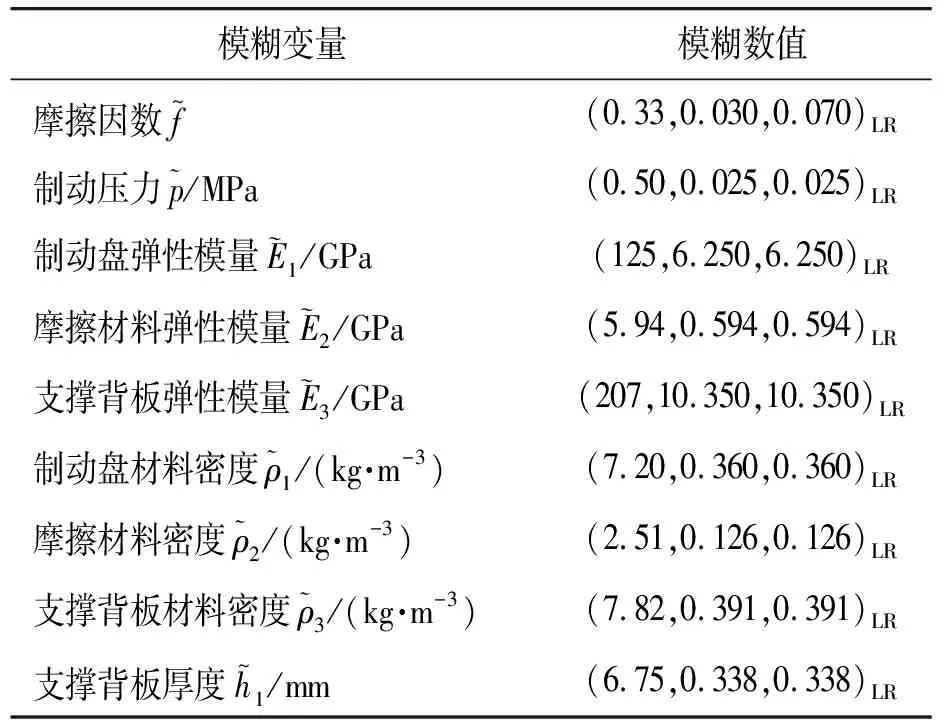
表2 系统模糊变量的取值

图5 模糊不确定性下的解集曲线

由文献[11]可知，工程设计中为保证制动器系统的稳定性，一般要求ζi≥-0.01。由图5可知，在给定的不确定性条件下，当截集λ∈[0.93，1]时，阻尼比响应均大于-0.01，系统的稳定性完全满足要求；而当截集λ∈[0，0.93]时，阻尼比响应既可能大于也可能小于-0.01，系统的稳定性不完全满足要求，稳健性较差。这说明在不确定性条件下需对系统的稳定性进行改进提高。