季艳秋，卢志义

(天津商业大学 理学院，天津 300134)

1 引言

贝叶斯推断是统计学习理论的重要组成部分。贝叶斯推断是从变量的先验分布出发，利用观察到的样本信息，根据贝叶斯公式得到参数的后验分布，从而对变量及其不确定性进行推断，进而做出决策的统计方法。贝叶斯推断在参数估计、模型评价与选择、概率隐变量建模等诸多统计学和机器学习领域具有广泛的应用。

在大数据背景下，贝叶斯机器学习通常采用概率隐变量模型，隐变量是模型中一些无法观测到的变量，它们虽然也是模型的一部分，但由于没有观测值，给贝叶斯后验分布的计算带来很大的不便。传统的做法是通过对所有隐变量进行求和或积分运算，从模型中“删去”隐变量，从而达到简化计算的目的。但对于复杂模型和大规模数据，以上方法面临严峻的挑战。主要表现在，由于模型中隐变量较多，可能达到数百万甚至数亿，对这些隐变量进行求和或积分运算显然是不可行的，即便可以依赖于现代计算机快速计算能力进行精确计算，但计算所消耗的时间代价是无法承受的。在这种情况下，变分推断(Varational Inference，以下简称VI)为贝叶斯推断提供了一种非常高效的近似替代算法。

设观测变量x和隐变量z的联合概率分布p(x,z)，此处的z包括模型的参数。贝叶斯推断的主要目标是计算隐变量z的条件密度函数p(z|x)，但该密度函数的显式表达是很难得到的。解决这一问题的方法可分为两类，即MCMC(Markov Chain Monte Carlo)方法和VI。MCMC抽样虽然已经成为现代贝叶斯统计不可或缺的工具，但在模型较为复杂或数据规模较大的情形下，MCMC抽样由于计算量大、收敛速度慢而导致计算成本偏高。VI的思路是在给定观测变量x的情况下，采用适当的近似方法，得到隐变量z的条件密度p(z|x)在某种意义下的一个近似。与MCMC方法最大的不同是，VI的主要思想不是使用采样，而是使用优化的思想和方法得到后验分布的近似。使用变分方法进行近似推断的优越性在于近似族的选择具有很大的灵活性，往往能够较好地接近精确后验分布，并且近似分布具有计算简单、稳健性强的优良特性。

VI改变了力求精确建模的传统认知，是贝叶斯推断在研究范式上的一种转变。特别是在大数据背景下，VI为贝叶斯推断提供了一种相对简单，但精确度和稳健性都能得到保证的新方法。近20年来，随着计算机技术的发展和大数据研究的兴起，VI愈加受到人们的关注，在许多领域得到广泛应用且具有良好的效果。然而，对VI的研究和应用主要出现在计算机学科及其应用领域中，并未受到统计学界的重视。本文在回顾VI发展的基础上，介绍VI的基本理论与算法以及在大数据领域的拓展算法，并对VI在大数据领域的应用与发展前景，以及未来的研究方向进行分析和讨论。

2 VI的基本理论

2.1 问题描述

设x={x1,…,xn}为一组数量为n的观测变量，将模型中所有感兴趣的未知变量都看作隐随机变量，记作z={z1,…,zm}，并设x与z的联合概率密度为p(x,z)，隐变量的条件密度为p(z|x)。贝叶斯推断所要解决的问题是根据观测值以及联合分布p(x,z)，计算隐变量的条件密度p(z|x)。

由贝叶斯公式，条件密度p(z|x)可通过下式得到：

(1)

式(1)中，分母是观测数据的边际密度，也称为证据(Evidence)。对于许多模型，该积分很难直接计算，或计算的时间成本太高，因此，希望找到一个相对简单的分布q(z|λ)来近似精确的后验分布p(z|x)，称这个近似分布为变分分布，其中λ={λ1，…,λn}为分布q(z|λ)的参数，称为变分参数。为简便，省略变分参数λ，用q(z)来表示变分分布。

2.2 证据下界

为了得到精确后验分布的候选近似分布，首先需要确定一个候选近似分布的变分分布族Q，其中的每个元素q(z)∈Q都是精确后验分布的候选近似分布。VI的目标是在某种“距离”下找到最优的候选近似分布q*(z)，使其近似真实后验分布p(z|x)的效果最好。

衡量近似效果常用的指标为KL散度(KL divergence)，也称为相对熵或信息增益。分布p(z)和q(z)的KL散度表示为KL(q(z)‖p(z))，其计算公式为：

(2)

KL散度是两个分布之间接近程度的度量，它是非对称的，即KL(q(z)‖p(z))≠KL(p(z)‖q(z))，并且是非负的，且当p(z)=q(z)时达到最小值0。

在KL散度下，VI问题转化为以下优化问题：

(3)

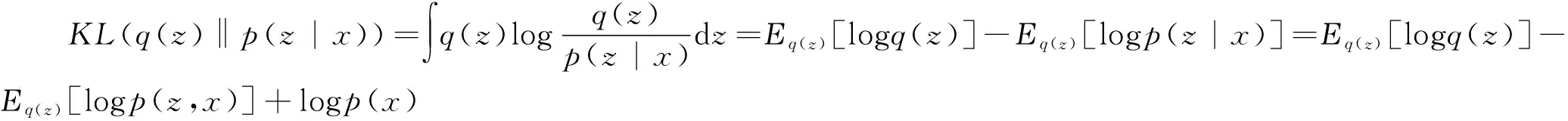
(4)

其中，Εq(z)[·]表示关于q(z)的期望，令

L(q)=Εq(z)[logp(z,x)]-Εq(z)[logq(z)]

(5)

则由(4)可得：

L(q)=logp(x)-KL(q(z)‖p(z|x))

称L(q)为证据下界(Evidence Lower Bound，以下简称ELBO)。对于任意的，由于KL散度是非负的，所以log(x)≥L(q)，即L(q)为对数似然函数(或证据函数)logp(x)的一个下界，这也是“证据下界”名称的由来。进一步，由(3)和(5)，并注意到logp(x)与q(z)的选取无关，所以最大化ELBO等价于最小化KL散度。

进一步，由(5)式可得：

L(q)=Εq(z)[logp(z,x)]-Εq(z)[logq(z)]=Εq(z)[logp(z)]+Εq(z)[logp(x|z)]-Εq(z)[logq(z)]=Εq(z)[logp(x|z)]-KL(q(z)‖p(z))

(6)

式(6)的第一项是对数似然函数的期望，第二项是变分分布与隐变量先验分布的KL散度。为了使证据下界达到最大，对数似然需达到最大，而变分分布与先验分布尽量接近。所以ELBO体现了传统贝叶斯统计的基本思想，即似然与先验之间的均衡。因此，在VI中，常采用ELBO作为目标函数来寻找最优的变分分布，因而，问题(3)的求解转化为以下最优化问题：

(7)

2.3 平均场VI理论

候选分布族的复杂性决定了VI中优化问题的复杂性，Q的不同选取方法会产生不同的VI理论和方法。最早也是最常用的VI理论是平均场VI(Mean-Field Varational Inference，以下简称MFVI)。在MFVI中，假定隐变量之间是相互独立的。独立性的假定可以简化VI的计算及优化过程，因此MFVI在诸多领域得到了广泛的应用。

平均场变分分布族(记为QMF)中的元素q(z)可以写成如下形式：

(8)

该形式中，每个隐变量zj都由变分因子q(zj)独立体现，因此这种结构也称为完全分解结构，这种结构可以通过简单的迭代更新来优化变分下界L(q)。

将(8)式代入(5)式，并利用变量间的独立性(即平均场假设)分解(5)式的第二项，同时，将与q(zj)无关的项作为常数项(记为cj)，可得到q(zj)的变分下界L(qj)的表达式：

Εq(zj)[Εq(z-j)[logp(zj,x|z-j)]]-Εq(zj)[logq(zj)]+cj=-KL(logq(zj)‖Εq(z-j)[logp(zj,x|z-j)])+cj

(9)

其中，z-j表示隐变量z中除去zj剩下的变量，Εq(z-j)[·]表示关于q(z-j)的期望。

由KL散度的定义及(9)式可知，问题(7)的最优解q(zj)为:

logq*(zj)=Εqz-j[logp(zj|z-j,x)])+c

(10)

其中，c为与优化无关的常数，对这个结果求幂并归一化得到:

q*(zj)∝exp(Εqz-j[logp(zj|z-j,x)])∝exp(Εqz-j[logp(x,z)])

(11)

以上优化VI的方法称为坐标上升VI算法(Coordinate Ascent Variational Inference，以下简称CAVI)。

3 VI的研究进展

20世纪80年代，Peter和Hinton等开始研究VI，并将此方法应用于神经网络中，以得到贝叶斯推断中后验概率分布的近似。1988年，Parisi[1]提出了平均场理论，将VI的部分统计特性与期望最大化算法相结合，使VI方法更具普适性，从而推动了VI的发展。之后，Hinton和Van Camp等在1993年提出了一种类似于神经网络模型的变分算法[2]，吸引了愈来愈多的学者在不同模型中应用VI算法。进入21世纪，随着计算技术的发展以及数据复杂性的增强，VI方法得到了迅速发展。下面从理论研究和实际应用两方面阐述VI的最新研究进展。

目前，在理论研究方面，VI方法的最新研究可以概括为以下四个方向。

在VI的准确性方面，变分分布的复杂性与推断的准确性始终是一对矛盾，因此在可承受的计算成本下，尽量提高推断的准确性，是VI研究的突破方向。Barber等[3]提出可积分的VI方法，提升了VI的计算准确度和速度； Mimno等[4]提出hybrid VI方法，提高了传统VI的性能；Huggins等[5]提出了VI中后验均值和不确定性估计误差的界限，提高了近似的准确性等。

为了提升VI方法处理大规模数据集时的效率，Hoffman等[6]提出随机VI方法(Stochastic Varational Inference，以下简称SVI) 。在每次迭代中，SVI方法只需要使用少量的样本计算目标函数的无偏梯度，就能在保证准确性的同时实现VI的快速优化；之后，一些研究进一步改进了SVI算法，如Ranganath等[7]在2013年提出具有自适应学习率的SVI方法，加快了SVI方法的收敛速度，又在2016年提出算子变分推理，允许推断扩展到海量数据；2020年，Tomczak 等利用一种新的再参数化技巧，提高了在大规模网络结构上使用VI方法的性能。

在实现VI的通用框架方面，Ranganath等[8]在2014年提出黑盒VI方法，该方法可在模型结构未知的情况下推导出梯度或进行分区函数评估；之后，Titsias等[9]在2015年提出一个关于随机VI的黑盒方法；2019年，Ruiz等在黑盒VI的基础上，使用重要性采样方法减小蒙特卡洛梯度的方差。这些方法使得非专业人士也能轻松的使用VI方法。

在放宽VI的独立性假设方面，为了考虑变量之间的相关性，并使目标函数可解，许多学者对此进行了大量的研究。Opper等在2009年提出了高斯推理方法；Hoffman等在2015年提出结构化的VI方法；同年，Han等提出高斯copula VI方法；Tran等在2016年提出copula VI[10]，等等。

在大数据背景下，得益于快速发展的计算技术以及便捷的统计计算软件，VI方法与各种统计模型相结合，被广泛于应用于各个领域，下面介绍代表性的应用成果。

在计算生物学方面，VI已被用于全基因组关联研究；调解网络分析、基因序列检测、系统发育隐马尔可夫模型、种群遗传学以及基因表达分析等。

在计算机视觉和机器人领域，VI所具有的能够快速推断的特性在视觉系统中起着重要作用。最早的例子包括推断非线性图像流形和在视频中寻找图像层。最近，VI在图像去噪、机器人位置识别和映射、以及图像分割[20]等方面的应用中也有很大的突破。

在计算神经科学方面： VI有着广泛的应用，包括多学科层次模型、空间模型、脑机接口以及因子模型，等等。特别是，该领域的研究人员还研发出了一个使用变分方法解决神经科学和心理学研究问题的软件工具箱。

在自然语言处理和语音识别方面：VI已被用于解决解析语义、语法归纳、流文本模型；主题建模、隐马尔可夫模型和词性标注等问题。在语音识别中，VI被用来拟合复杂耦合的隐马尔可夫模型等。

VI还有许多其他的应用。包括市场营销、强化学习、统计网络分析、天体物理学和社会科学等，并且，开发了各种类型的模型，如收缩模型、一般时间序列模型、稳健模型和高斯过程模型等等。

4 大数据背景下VI的拓展：SVI

经典的平均场VI在历史上一直发挥着重要作用。然而，在大数据背景下，经典VI算法的计算量会变得非常庞大。即便是上文所述的坐标上升VI算法，随着数据量的增长，每次迭代的计算量也会大幅增加，影响了其在大数据处理中的应用。Hoffman等提出的SVI算法，在每次迭代中采用少量的样本就可以得到目标函数的无偏梯度，可以大幅减少计算量，因而适宜于大规模数据情形下的VI。

指数族分布是贝叶斯统计和机器学习中经常用到的一类统计模型，指数族模型中常见的是由参数和隐变量组成的条件共轭模型，本文以条件共轭模型为例介绍SVI算法的基本思想。

4.1 条件共轭模型

考虑上文中的条件共轭模型，设β为模型参数，则模型所有变量的联合概率密度为：

(12)

为了确保式(12)中的联合概率密度服从指数族分布，首先假设以β为条件的每对(xi,zi)的联合密度函数具有指数族分布的形式:

p(zi,xi|β)=h(zi,xi)exp{βTt(zi,xi)-a(β)}

(13)

这里t(·，·)的是该分布的充分统计量。同时，假设参数的先验分布就是相应的共轭先验：

p(β)=h(β)exp{αT[β,-a(β)]-a(α)}

(14)

这里假设参数的先验分布具有自然(超)参数α=[α1,α2]T，α为一列向量，并且为充分统计量。使用共轭先验，可以使式(12)中的联合概率密度服从指数族分布，且自然参数的估计值为[1]：

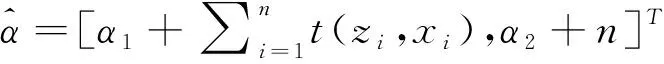
(15)

由式(12)可知，给定β和xi，隐变量zi条件独立于其他隐变量z-i和其他观测数据x-i，z-i表示隐变量中除去第i个隐变量以外的变量，x-i表示观测变量中除去第i个观测变量以外的变量，于是有：

p(zi|xi,β,z-i,x-i)=p(zi|xi,β)

(16)

由式(13)的局部似然项p(zi,xi|β)的性质，进一步假定上式的分布为指数族分布，具有形式

p(zi|xi,β)=h(zi)exp{η(β,xi)Tzi-a(η(β,xi))}

(17)

将以上所定义的模型称为条件共轭模型。

4.2 条件共轭模型的CAVI算法

上节所描述的条件共轭模型可以采用CAVI算法进行变分推断。用q(β|λ)表示β的变分后验近似密度函数，其中，λ为全局变分参数。用q(zi|φi)表示隐变量zi的变分后验密度函数，其中φ={φ1,φ2,……,φn}为局部变分参数。CAVI通过交替更新局部变分参数和全局变量参数进行迭代，从而优化ELBO，当ELBO的值收敛时，停止迭代。其中局部变分参数的更新公式为：

φi=Ελ[η(β,xi)]

(18)

全局变分参数的更新公式为：

(19)

将(12)中的联合概率密度以及相应的平均场变分密度代入式(5)，并省略与变分参数无关的项，可得每次迭代中ELBO的计算公式：

(20)

其中，

(21)

4.3 条件共轭模型中ELBO的随机优化

在基于梯度法的优化问题中，自然梯度以一种可感知的方式扭曲了原有的参数空间，使得在新的空间中，参数在不同方向上的变化量相同时，相应的KL散度的变化量也保持相等，因而采用自然梯度可以提高优化问题的效率。

在指数族模型中，在欧氏梯度的基础上乘以费雪信息矩阵的逆f(λ)-1可得到参数的自然梯度。Hoffman等得出ELBO的欧氏梯度为[23]:

(22)

从而，可得到自然梯度g(λ)的计算公式为：

(23)

显然，自然梯度除了具有良好的理论特性外，要比欧氏梯度更容易计算。

若在ELBO的优化中采用自然梯度，全局变分参数的迭代公式可写成：

λt=λt-1+εtg(λt-1)

(24)

其中εt为步长。将式(23)代入式(24)中，可得：

(25)

式(25)表示在每次迭代中，首先进行坐标更新，然后将当前估计调整为更新后的坐标和前一次迭代中变分参数的值的加权组合。

在计算条件共轭模型的自然梯度时，除了计算坐标上升更新外，不需要其他计算。SVI是利用自然梯度并结合随机优化算法来解决大数据情形下优化算法的计算复杂性问题的。研究表明，只要步长序列满足一定的条件，SVI就可以使用有噪声但无偏的梯度来优化目标函数ELBO，从而使得机器学习方法能够拓展到大数据领域[24]。

SVI首先构造一个计算成本低、有噪声、无偏的自然梯度。将(15)代入(23)得到：

(26)

通过从(1,……,n)上的均匀分布中抽取样t，构造一个有噪声的自然梯度：

t～Unif(1,……,n)

(27)

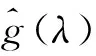
为使以上算法收敛，步长序列需满足一定条件：

(28)

通过SVI算法，可以在大数据背景下快速优化ELBO，获得较为准确、稳健的变分近似后验。

5 总结与展望

VI使用优化方法来近似目标概率分布，其目的并非求出精确概率分布的解析形式，而是找到近似度高、计算相对简单、稳健性好的近似分布。VI适用于大规模数据集以及希望快速探索大量模型的场景。VI改变了人们精确求解隐变量概率分布的传统认知，是对经典贝叶斯理论的有益补充。从20世纪八九十年代第一次提出VI方法至今已有30多年历史，近年来，VI方法得到了快速发展，渐趋成熟。同时，随着大数据的兴起，VI的应用领域也愈加广泛。本文回顾了VI的发展历程，介绍了VI的基本原理，并综述了大数据背景下VI的拓展。

面向未来，VI无论在理论上还是在应用上，仍有许多尚未解决但很有研究空间的问题。作为本文的结束，提出VI未来需要进一步研究的问题和方向。

5.1 开发更好的分布间近似程度的度量指标

本文重点介绍了使用KL散度度量两个分布之间的近似程度的VI问题。然而KL散度不具有对称性，这在某种程度上影响了VI的研究与应用。因此开发更好的度量分布间近似程度的指标，是VI在理论研究方面的重要方向之一。

5.2 改进平均场VI中的独立性假设

虽然平均场VI方法很灵活，在实际中得到了广泛的应用，但平均场方法是建立在严格的独立性假设的基础之上的。独立性假设虽然有助于简化计算、便于优化，但大大限制了变分分布族的选择范围，从而导致低估后验方差等问题。因此，如何在保持优化方法有效性的同时，考虑不同分量之间的相依性，以得到更好的近似后验分布，是未来的重要研究方向。

5.3 VI与MCMC结合

VI与MCMC是估计隐变量条件密度的两种不同方法，一个自然的问题是，能否将两种方法结合起来，既可以利用MCMC在估计准确性方面的优势，也能发挥VI在计算成本方面的优势。近年来，一些文献对此问题进行了初步的探讨。例如，Zhang等将MCMC与VI结合在一起，不仅能准确、有效地逼近后验图像，而且有利于进行MCMC和Gibbs采样过渡的随机梯度设计；Francisco等[11]通过运行几个MCMC步骤来改进变分分布，获得了更好的预测性能。可以预见，在理论上进一步研究VI与MCMC结合的问题，将是未来理论和实践方面的重要研究课题。

5.4 VI的统计特性

从统计学的视角，对于MCMC，统计学者已对其进行了大量的研究，取得了丰硕的理论成果。但是，鲜有文献对VI的统计特性进行探索，例如，当用变分分布代替真实后验分布时所产生的近似误差大小的度量，以及采用近似分布进行预测时预测误差的度量问题。因此，从统计学的角度，对VI进行系统而深入的研究是未来的重要研究方向。