曹相波

（大理州实验中学数学组 云南大理 671099）

一、问题引入

在解三角形中，我们经常会碰到已知对边对角求关于另两边的关系式的最值或取值范围问题，比如求面积或周长的取值范围。对于这类题，一般结合基本不等式可以解决，但利用不等式只能解决最大值问题，而最小值方向就需要其它知识解决，另外，如果当另两边前的系数不相等时的线性关系式求最值就不能简单解决。

又△ABC中，a+c＞b=2 ∴2＜a+c≤4 ∴l=b+a+c=2+a+c∈（4，6］

从上例的解法，能看出基本不等式在求最大值方向问题不大，但对于求最小值方向就存在麻烦，需要结合其它隐含条件，比如，在求周长最小值方向时，需要考虑在三角形中两边之和大于第三边这一隐含条件。那有没有能直接求出最大和最小两个方向的值呢？

二、问题探究

当然，在解三角形中，很多同学是正弦定理或余弦定理轮换使用来寻求解题方法，下面我们就用正弦定理尝试一下。

解：由正弦定理可得：

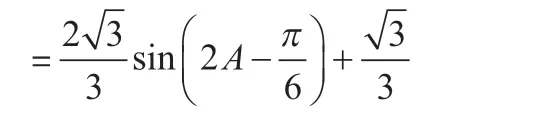
【注：三角函数中利用公式化简是高中数学的基础，中间过程就留给读者自行解决，以下也是如此】

从以上方法中可以看出，用正弦定理转化到用角表示边长之后，求三角形面积或周长问题就化归到三角函数求最值问题上来，并且最大和最小方向的值都可以直接算出来。

三、问题变式

当然，有些时候题目条件可能会加强。比如在其它条件不变的情况下，将△ABC限定为锐角三角形时，求其面积S和周长l的取值范围。锐角三角形这一条件的运用往往考虑最大角是锐角。

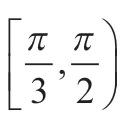
四、问题变式反思

那么，点B运动到什么位置时，△ABC的面积S和周长l取得最值？

借助于圆的对称性，可知当点B与点M重合时，△ABC的面积S和周长l取得最大值；当点B无限接近于点A或点C时，△ABC的面积S和周长l趋近于最小值（为保证△ABC的存在，点B不能与点A或点C重合，故用趋近于一词）。

在其它条件不变的情况下，将△ABC限定为锐角三角形时，则点B只能在点D和点E之间（点B不能和点D或点E重合）运动（AD和CE为直径，∠CAE和∠ACD为直角）。

综上，可以得到一个结果，△ABC的面积S和周长l都是在垂直平分于边AC的直径的端点M点处取得最大值。

五、方法推广

从上面的数形结合分析能够让我们更加形象地理解题目的内涵。基于对原题的深入理解我们就可以更好地利用这些思想方法去破解对应的变式题。下面就对变式题型进行研究。

（一）已知角非60度

该题只对已知角大小做出改变，方法不变，用余弦定理结合基本不等式或者正弦定理用某个角表示未知边转化到三角函数求最值这两个方法都可以（具体过程请读者自行完成）。

另外，我们结合外接圆来研究一下。如图2。

设两腰长为x，则由余弦定理可得

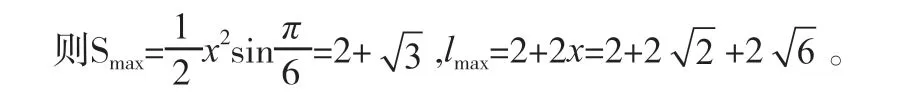
（二）求解另两边的一次关系式（xa+yc）的最值

解：由正弦定理得a,c与第二部分问题探究相同（故省略）

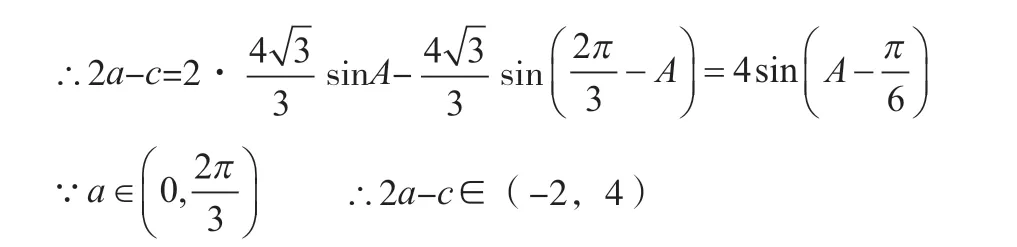
（三）已知非对边对角

例题3：（2019年全国三卷第18题）

（1）求B； （2）若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围.

解：（1）过程略可得B=60°.

由于△ABC为锐角三角形，故 0°＜A＜90°，0°＜C=120°-A<90°，所以30°＜C＜90°，

下面我们借助于图形研究一下第二小题。

如图3.由于△ABC为锐角三角形，则需考虑最大角为锐角即可。

当∠B=60°为最大角时，△ABC只能为等边三角形，即为图3中的△ABM。

当∠A为最大角时，点C在点M与点E之间运动（不包含点E和点M）。

当∠C为最大角时，点C在点M与点D之间运动（不包含点D和点M）。

综上，当△ABC为锐角三角形时，点C在点D与点E之间运动（不包含点D和点E）。

由图可得：S△ABD＜S△ABC＜S△ABE。

六、方法总结反思

从本文分析可以看出，相对于利用不等式求最值，利用正弦定理用角表示边长从而转化到三角函数求最值的方法更具有优势，更具有普遍适用性，可以称作是解三角形求范围问题的通法，当然结合外接圆来分析此类题目，让我们更加形象地理解其内涵。