杨克林

(福建省漳浦第一中学 363200)

三角函数习题类型灵活多变，解题的思路也有所不同.其中运用三角函数性质、运用辅助角、运用均值不等式以及换元法是解题中较为常用的方法.教师授课中为使学生掌握不同方法的具体应用，使其更好地把握解题中的相关细节，应注重为学生做好解题示范.

一、运用三角函数性质求最值

运用三角函数性质求最值的思路为：其一，灵活运用相关的诱导公式等将函数表达式整理成y=Asin(ωx+φ)+h(或y=Acos(ωx+φ)+h)的形式；其二，根据已知条件找到ωx+φ的取值范围；其三，联想所学的三角函数单调性知识，在给定的定义域中求出最值.

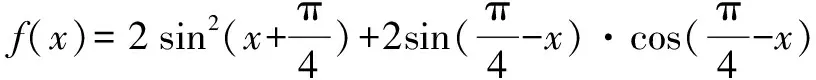
题目给出的函数f(x)的表达式较为复杂，解答该题时的第一印象便是先使用诱导公式、两角和差公式、降幂公式、辅助角公式等将函数f(x)的表达式化简成类似“y=Asin(ωx+φ)+h”的形式.而后根据给出的定义域区间，采用整体思想结合三角函数图象，分析其在对应区间上的单调性，求出函数最小值即可.

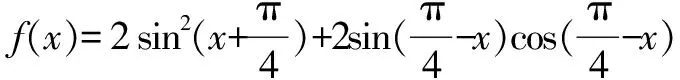
=sin2x+cos2x+1

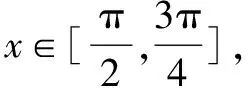
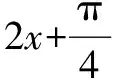
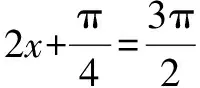
二、运用辅助角求最值

运用辅助角求最值应牢记辅助角构造公式，尤其应明确引入的角度与条件之间的内在关联，通过运用已知条件求解出未知参数，而后运用三角函数的边界性确定最终结果.

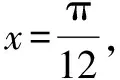
题目中函数f(x)的表达式并不复杂.根据经验，需要引入辅助角θ进行化简，化陌生为熟悉.同时，结合已知条件中函数对称轴以及三角函数图象特点，确定对称轴的表达式，而后将已知条件代入，计算出ω的值.最后利用辅助角之间的关系，求出a的值，问题便可迎刃而解.

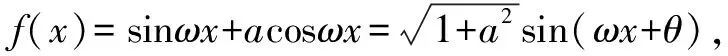
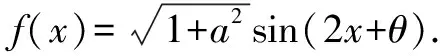
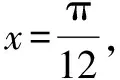
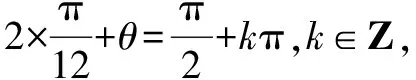
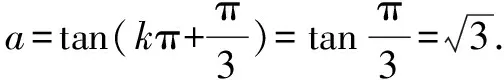
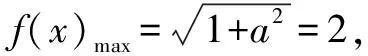
三、运用均值不等式求最值

均值不等式常用于求解三角函数最值.为保证解题结果的正确性，运用均值不等式时应注意把握参数的取值范围，牢记均值不等式成立的条件，尤其针对无法使用均值不等式的习题， 应注重结合已知条件对相关的角度进行拆分，凑成能够运用均值不等式的形式.当然等号成立的条件应保证参数能够取到.

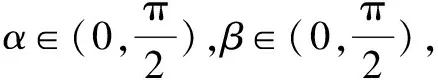
习题题干简洁，认真分析已知条件以及要求解的问题，可知需要对角进行合理的拆分，以便更好地借助两角和与差的三角函数知识进行化简.同时，积极联系所学，巧妙地运用两个角度的值配凑出对应的均值不等式，求出cosβ的最小值，尤其要注重分析均值不等式等号成立的条件，保证推理的严谨性.

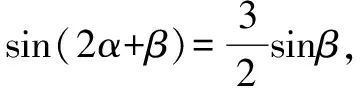
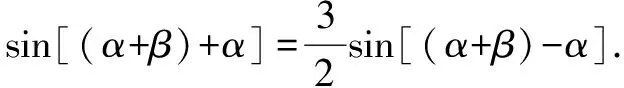
所以sin(α+β)cosα+cos(α+β)sinα

整理,得sin(α+β)cosα=5cos(α+β)sinα.

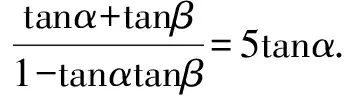
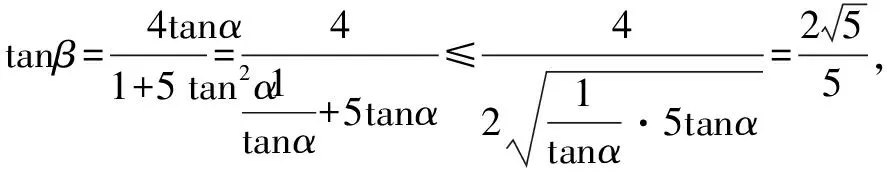
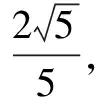
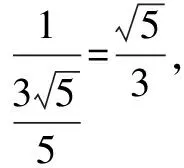
四、运用换元法求最值

运用换元法求解三角函数最值具有一定的技巧，求解时需要先对已知条件进行转化，而后进行合理地换元.当然换元前后参数的取值范围不能发生变化.而后联系所学的函数知识求出最值.

例4已知A,B,C为锐角ΔABC的三个内角，且满足tanB+tanC=2tanBtanC，则tanAtanBtanC的最小值为( ).

A.2 B.4 C.6 D.8

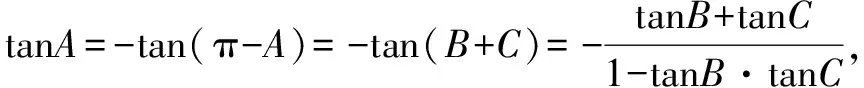
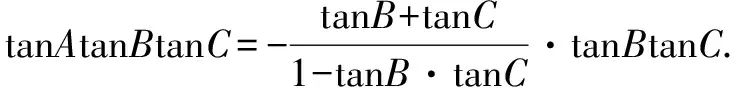
又因为tanB+tanC=2tanBtanC，

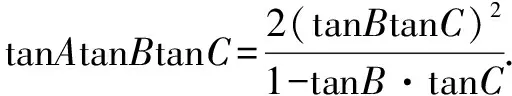
令t=tanBtanC，因为A,B,C均为锐角，因此tanA>0，tanB>0，tanC>0.

所以1-tanBtanC<0，则t>1.

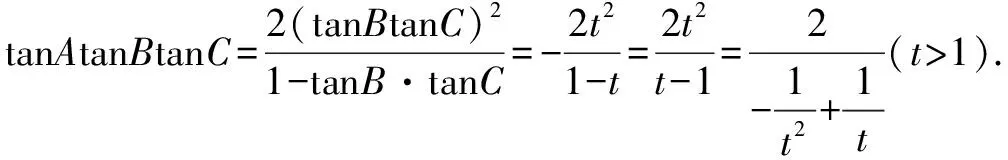
故tanAtanBtanC≥8，其最小值为8，此时t=2，故选D.

三角函数最值问题在高考中的出现频率较高，考查的知识点较多，解题思路灵活多变.解题时只有找到正确的思路，才能高效地加以解答，因此教师授课中为提高学生解答三角函数最值问题的能力，应结合自身教学经验，为学生讲解经典习题，并与学生一起分析解题思路，展示具体的解题过程，在学生头脑中留下深刻印象.同时课堂上注重预留一定的空白，鼓励学生做好听课总结，对相关题型分门别类，认真分析相关的解题思路，在平时的训练中加以灵活运用，实现解题能力更好的提升.