赵友国，刘尚伟，王冠中，徐海柱，李富伟，逄 春

（1.东方电子股份有限公司，山东 烟台 264000；2.浙江大学 电气工程学院，杭州 310008）

0 引言

大规模随机波动的新能源发电设备正广泛改变传统可控/可计划的电网运行模式，其中，新能源并网功率的随机性、间歇性导致电力系统的运行状态难以准确估计，对EMS（能量管理系统）的功能实施带来了挑战[1]。量测数据的可观性分析是保证状态估计有效实施的前提，当量测数据不完全可观时，可以提供可观孤岛等信息，进而指导量测装置的选址，以实现系统量测数据的完全可观。有必要指出，随着中国电力事业的快速发展，高压网架的可观性已满足状态估计需求，但对于海量节点的中低压网架，特别是配电网络，由于节点数量大、投资成本高，当前尚未将数据测量覆盖至每一个节点，因此仍有必要研究状态估计的可观性问题，这对于构建成本可控的配电网络状态估计系统具有实际意义。

针对状态估计可观性分析的研究可以追溯到上世纪70 年代，E.E.Fetzer 等将现代控制理论中的可观性概念引入到电力系统静态状态估计问题，通过将线性系统中的动态过程置零，证明了电力系统静态状态估计的可观性本质上与线性系统可观性保持一致[2]。

可观性分析的方法主要分为图论类方法和数值计算法。电力系统静态状态估计的可观性概念建立以后，首先发展的是图论类方法[3]。图论类方法将量测装置获得的数据与输电网络的线路相互关联，通过量测装置数据覆盖到的线路能否组成连通树来判断系统的可观性。图论类方法几乎不用进行数值计算，具有形象直观、应用简单的优势[4]，但其所得结果不能与数值计算保持完全一致，导致在一些复杂场景下结果不够准确[5]。数值计算法直接对状态估计方程组的雅可比矩阵H[6]及其增益矩阵HTH 或者Gram 矩阵HHT[7-8]进行分析，检验矩阵是否奇异，若奇异则认为系统不完全可观。但考虑到实际系统的雅可比矩阵具有非常高的维数，且不具有稀疏性，因此数值计算法面临的主要挑战是计算效率低。为提高数值计算法的效率，目前主要采用两类研究办法，分别是迭代法[9-10]和直接法[5]。迭代法通过迭代求解部分状态变量的方式完成对增益矩阵或Gram矩阵的分解，并从结果中直接判定系统是否完全可观。直接法则不进行状态变量的计算，转而对矩阵直接分析，当分析对称矩阵如增益矩阵或Gram 矩阵时多采用矩阵三角分解的方式[7-8]，而对非对称矩阵如雅可比矩阵进行分析时多采用行/列变换的形式[11]。

为了进一步降低状态估计可观性分析的计算负担，本文从正交分解角度提出一种可观性分析的直接法，该方法仅涉及到线性代数理论，便于工程应用[12-14]。主要思路是将雅可比矩阵行空间进行正交分解得到一组正交基，正交基的快速构造利用了启发式方法，若正交基的维数与状态变量的数量一致，则系统完全可观，否则需要补充量测数据，而量测数据的筛选也是通过正交分解的办法进行选择。最后通过标准算例验证了所提方法的有效性。

1 旋转变换与正交分解

从数学角度介绍所提算法的原理。按照从一般到特殊的顺序，首先介绍旋转变换，在此基础上介绍线性空间关于向量、子空间的正交分解，最后阐明施密特正交化与正交分解之间的联系。

1.1 旋转变换

旋转变换具有广泛的应用领域，如高斯消元等，了解其定义有助于深入认识很多常见算法的共有属性[15]。旋转变换的定义式如下所述。

由式（1）可知，旋转变换由两个步骤组成，第一行是对作为旋转轴的向量进行标准化，改变其大小；第二行代表旋转，将Hj中其余向量减去标准化后的旋转轴向量的倍。

1.2 正交分解

假设存在向量uj≠0，令（向量uj和的内积），k=1，…，n。若，则有下面结果成立：

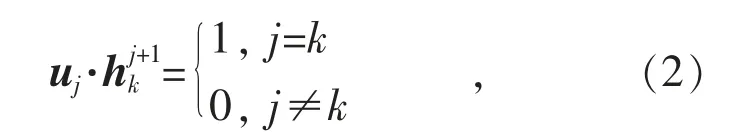
式中：L（Hj）⊥为从子空间L（Hj）中分解出的关于向量uj正交的子空间，又称uj的正交补空间。

下面介绍子空间L（Hj）关于子空间L（{u1，…，un}）的正交分解。

假设有子空间L（{u1，…，un}）。按照下标顺序依次对u1，…，un和L（H0）执行正交分解步骤，可获得L（H0）中关于L（{u1，…，un}）正交的子空间。具体地，若令并且，则：

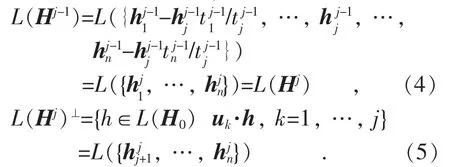
可知，若对L（H0）和u1，…，uj依次执行正交分解步骤，那么余下的就是子空间L（{u1，…，uj}）的正交补空间。此外，还有另外一个性质，即：

式（6）说明hj与uj除外的所有ui，i≠j 正交。

1.3 施密特正交化

给定子空间L（H0），其中，向量线性无关，目标是得到L（H0）中一组单位正交基，则施密特正交化过程可以描述如下：

由步骤（1）—（3）可见，本文介绍的正交分解与施密特正交化具有类似对偶的关系，即正交分解是根据给定的L（{u1，…，un}）来求取其在L（H0）中的正交补空间，而施密特正交化则是从L（H0）的一组基中找到相互正交的{u1，…，un}。

通过本文对旋转变换、正交分解的介绍，可以加深对施密特正交化的认识，尤其是关于正交化与正交补空间的关系的认识，有助于直观理解下文所提可观性算法的原理。

2 状态估计与可观性分析

高、中压交流电网状态估计的重点在于计算节点电压的相角，故一些文献采用直流潮流模型来进行状态估计及其可观性分析，因此量测方程可表示为：

式中：H∈Rm×n为有功雅可比矩阵；θ∈Rn为节点电压相角向量；z∈Rm为SCADA（数据采集与监控）系统的测量数据。当系统配置有PMU（同步相量测量单元）时，z 中包含部分节点相角θ 的测量值或两个节点相角差，此时H 中对应一行有唯一非零元1 或两个非零元+1，-1。n 为测量数据和状态变量的维数，m 为实际量测数据的维数。矩阵H 具体表示为向量形式如下：

式中：hi，i=1，…，m 为矩阵H 的行向量。

可观性分析的目的在于判断量测方程的数据采集是否满足计算节点电压相角向量θ 的要求，否则需要补充量测数据并增加方程组的方程数。当量测方程完全可观时，矩阵H 所张成的线性子空间将具有n 个正交基；若矩阵H 不可观，从子空间中找到的正交向量组可用来恢复可观性或计算可观性孤岛。下面介绍的可观性分析算法便是上述思路的具体展开。

可观性分析算法的输出结果主要分两方面，一方面是确定矩阵H 行向量中的线性无关部分，另一方面是给出矩阵H 行空间的一组正交基。若线性无关的向量数等于状态变量数，那么系统完全可观，并且余下行向量代表冗余的量测数据。

本文所提可观性分析算法的具体步骤如下：

（1）首先初始化向量j=[j1，…，jm]T=0 和子空间X=span{0}。

（2）从矩阵H 中任选一行向量hk标准化为，令X1=span{u1}，j1=k。

（3）计算H 行向量（除hk以外）到子空间X1的投影，记投影为，以及投影与原向量的误差（或者说是hi到子空间X1的距离），记为，i=1，…，m。

（5）对向量组{u1，hj2}作施密特正交化处理，即，以及，进而得到子空间X2=span{u1，u2}。若对X2重复步骤（3）—（4），同理可得j3和hj3。

（6）继续上述步骤，给定向量组{u1，u2，…，hji}，并对上述向量进行施密特正交化，可得对应的子空间Xi=span{u1，ui}。

（7）对于j=1，…，m，向量hj对子空间Xi的投影为。

从几何的角度看，上述算法步骤（2）—（10）本质上是从H 行向量中选出距离子空间最远的一个作为新的基，将其加入子空间Xi并再次施密特正交化为一组新的正交基Xi+1，周而复始，得到H 行空间的一组正交基。利用最大距离来选择行向量是一种启发式方法，该方法的优点是计算负担小，因此可加快可观性分析的速度。

从代数的角度看，上述步骤（2）—（10）与矩阵的QR 分解[7]在形式上十分接近，最大不同在于本文算法将雅可比矩阵H 的行向量重新进行了排序，因此避免了矩阵求逆的操作，此外，也避免了矩阵迭代过程中由于部分行接近0 而附加的旋转变换。

此外，联系本文第一节的旋转变换与正交分解的理论背景可知，所提算法过程不改变原始矩阵H 行空间的维数，因而算法输出的正交基的数量恰是行空间维数，若其与状态变量数量一致，则系统完全可观。

3 重构可观性的量测数据选择方法

当系统为不可观系统且雅可比矩阵的阶数为n-r 时，上述算法可用于补充筛选r 个量测数据来重构可观的系统或n 阶雅可比矩阵。此时，经过步骤（1）—（10）所筛选出的正交的量测数据集合为Xn-r=span {u1，u2，…，un-r}，然后，以Xn-r为初始数据对其余量测数据所构成的雅可比矩阵Hc继续执行算法步骤（6）—（10）直到筛选出的正交量测数据的数量达到n。至此，通过上文所提算法实现了不可观系统的可观性重构。

4 仿真分析

4.1 5 节点系统算例分析

仿真分析的主要目的是验证基于正交分解的可观性分析算法的有效性。首先采用某5 节点系统[16]拓扑验证算法流程及结果的正确性，其量测装置配置如图1 所示，其中，3 号和5 号节点注入功率数据可测，线路4-5 和线路1-5 的有功潮流可测。

图1 5 节点系统

根据图1 中的测量装置配置情况，该系统的状态估计雅可比矩阵H 为：

矩阵H 的四列分别对应节点1，2，4，5 的状态变量（电压相角），节点3 为平衡节点故不在此列。本文所提算法初始向量为矩阵H 的第一行，对应节点3 的功率注入量测数据，此时有u1=[0，-0.71，-0.71，0]和j1=1。接着计算其余三行到X1=span{u1}的投影，可得对应的误差分别为。最大误差对应测量数据P5，继续执行算法流程，选择向量h2，且j2=2，经施密特正交化后得u2=[-0.43，0.21，-0.21，0.85]。计算矩阵H 的最后两行向量到X2=span（u1，u2）的投影及误差，。上面两个误差值相等，可选矩阵H 的最后一行h4，对其进行施密特正交化后得u3=[-0.75，-0.45，0.45，-0.15]，计算h3到X3=span（u1，u2，u3）的投影及误差，得，算法执行到终止判据。最后输出结果为j=[1，2，4]T，结论是系统不完全可观。

若继续补充量测数据以恢复系统可观性，那么根据上面得到的X3=span（u1，u2，u3），计算候补量测数据到X3的投影与误差，继续执行算法的（6）—（10）步，即可选择最少的候补量测数据来恢复系统可观性。新增加的量测数据雅可比矩阵为：

重构可观性算法运行后P2被选择用于恢复可观性。

4.2 118 节点系统的算例分析

通过118 节点系统[16]进一步说明本文所提算法的计算效率。当迭代次数达到117 时，此时的收敛误差为0.86，增加一次迭代后误差收敛到5×10-5，继续增加一次迭代误差收敛到1.5×10-7，此外，当前集合中正交的量测数据数量已经达到118。由于118 节点系统的雅可比矩阵阶数不超过118，因此继续增加迭代次数失去必要性。从迭代次数可见本文所提算法对于大规模电力系统拓扑具有良好的适应性。

最后，有必要指出本文所提算法从矩阵行空间的角度进行迭代，迭代次数不超过矩阵的行数，而以文献[6]为代表的算法需将Gram 矩阵或增益矩阵进行多次矩阵分解，每一次分解都需要将矩阵中的每一行进行变换进而实现对角化或稀疏化，因此本文所提算法对于行向量的运算次数最少。

5 结语

本文提出了一种基于正交分解的状态估计可观性分析方法，该方法属于直接法，从雅可比矩阵行空间及其正交基的角度，依托投影距离筛选量测数据，简化了可观性分析的计算过程，便于实际工程应用且易于被工程人员掌握。通过算例分析验证所提方法的有效性。