陈泽

(四川大学网络空间安全学院，成都610207)

0 引言

云计算可以协调大量计算机资源，从而提供给客户强大的存储和计算能力，大大提高计算资源的利用率。然而云计算也带来了新的安全问题：云平台可能错误执行客户的应用程序或者安全性无法保证，甚至其自身存在恶意行为，这些都可能侵害到客户数据的隐私性以及完整性以及计算结果的正确性。传统的方法，例如审计依赖于发生错误的频率，而冗余计算无法解决服务器之间相互串通的情况[1]。相比之下，可验证计算协议能够为用户提供一种无需重新本地运行在服务端所部署的程序也可验证结果正确与否的途径，且错误结果通过验证的概率是几乎可以忽略的。然而，虽然可计算协议在近些年来已经有了很大的进展，但适用于任何场景的可验证计算协议的性能开销仍与可应用阶段存在很大的距离。另外，随着同态加密技术的发展，基于同态加密算法构建一个可实现的适用于特定场景的可验证计算协议已成为可能。

矩阵乘在科学以及工程领域中十分普遍。对两个l×l的矩阵而言，传统的算法计算其乘积的复杂度为O(l3)。随着数据量的增大，l可能会达到几万甚至更高，而此时计算其乘积的空间以及时间开销都是个人计算能力难以承受的。本文在现有的基于格理论的同态加密算法基础上，构建了一个具有隐私保护的用于矩阵乘的可验证计算协议。由于格理论上的问题在量子计算机下仍是难解的，本文的协议具有抗量子分析的安全性以及隐私性，且本地的计算开销远小于直接计算矩阵乘所造成的开销。

1 设计原则和研究现状

(1)正确性。在服务器诚实且正确地执行Compute算法的情况下，Verify算法接受服务器返回的结果，且在解码后正是客户端所外包的计算任务的正确结果；

(2)安全性。即可验证性。由于硬件的故障或者软件的漏洞等意外原因，或服务器本身是敌对的或者自私的，其返回计算结果可能是错误的。安全性要求一个错误的结果能够成功欺骗Verify算法的可能性是可忽略的。

(3)高效性。可验证计算协议所产生的本地的计算开销应低于所外包的任务的开销。对矩阵乘的应用场景而言，协议所需的本地计算量应低于O(m3)。

除此之外，隐私对于个体以及商业公司来说，也是十分重要的问题。用户在外包过程中的原数据可能是敏感或者机密的，一些好奇的或带有恶意的云端可能会将这些数据存储起来以备后用。除以上性质外，一个具有隐私保护的可验证外包协议还应具有隐私性，即敌手在多项式时间内分辨出由已知明文和随机串产生的密文的概率是微乎其微的。接下来我们介绍国内外现有的针对矩阵乘的可验证计算协议。

Atallah等人于2010年提出了一种可以用于矩阵乘法的可验证计算协议[3]。该方案主要基于Shamir密钥分享协议。用t表示Shamir密钥分享协议中多项式的次数，对于每个要计算乘积的矩阵对，该协议需要生成16t+4个矩阵对。除此之外，对服务器返回的结果，客户端需要利用插值法依次还原出每个元素，因此该方案的计算复杂度为O(t2m2)。

Mohassel于2011年提出了一种针对矩阵乘法的可验证计算协议[4]。文中使用同态算法(GHV或者BGN)对明文矩阵A和B加密，并将密文发送至服务器；在服务器返回计算结果后，客户利用私钥对其解密获得矩阵C。之后客户生成m维随机向量v，并验证ABv=Uv是否成立。如果成立，则接受该计算结果。总体来看，该方案中客户的计算开销主要来自于其基于的加密算法对矩阵的加密和解密运算。然而其基于的GHV算法的复杂度为O(m3)，与矩阵乘法复杂度相当。后来在文献[5-6]中提出的协议中也应用了此类验证方式，然而文献[5]中仅对原矩阵进行了随机的行列变换，文献[6]中利用随机的掩码矩阵与原矩阵相加来保护用户的数据，这样的方式并没有严格的安全性证明，其隐私性以及安全性都是没有保证的。

除此之外，在文献[7-8]中提出的基于双线性对的验证算法实现了公开验证的性质，即客户可以将验证的工作交给公开的第三方，第三方在无需获知用户私钥和原数据的情况下可以验证结果的正确性。该性质虽然有一定的实用意义，但也为客户带来了很大的额外开销，包括生成满足双线性性质的群，以及对每个元素分别预处理所带来的O(m2)次幂运算。

由表16知，回归方程为：Y=261.509+6.495X1+2.133X2+0.426X3-0.605X4.

2 协议描述

本文中矩阵和向量分别用加粗的大写字母和小写字母表示(例如矩阵A，向量a)。用n表示安全参数，q=poly(n)为模数，Z表示整数集，Zq表示有限域Z/qZ。定义M次分圆多项式ΦM=xd+1，其中M为2的幂次，d=φ(M)=M/2。定义R=Z[x]/ΦM，Rq=Zq[x]/ΦM。定义以下分布：χk表示多项式的系数向量在{-1，0，1}d均匀分布；χσ表示多项式的每个系数选自标准差为σ的离散高斯分布。

为了构造用于矩阵乘的可验证计算协议，我们首先引入Halevi等人于2018年提出的同态加密算法HPS18[9]。该算法是在Fan、Vercauteren所提出的同态加密算法[10]基础上的RNS变种，其算法结构和运行效率较原算法都有了较大的优化提升。该算法的安全性基于环上的误差学习问题(Ring Learning with Errors，RLWE)：用χ表示R上的某个分布，对于e←χ，s∈Rq，在多项式环Rq均匀选取(a，b)，RLWE问题指分辨(a，b)和(a，(a，s)+e)两个分布是困难的。HPS18加密算法的具体步骤如下：

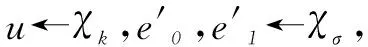
c) Decsk(c)：对于密文c=(c0，c1)，计算h=[c0+c1s]q，还原明文m=[(x·p/q)]p。

d) EvalAddevk(c1，c2)：对于输入的两个密文c1和c2，其同态加的结果为[c1+c2]q；

本文用于矩阵乘的可验证计算协议构建在上述算法之上。在下面描述中，使用矩阵X，Y∈Rl×l表示明文的数据；外包给服务器的函数为计算H=XY。我们的协议具体步骤如下：

a) KeyGen(1n)：安全参数为n，用户端调用KeyG(1n)生成公私钥对(sk，pk)以及计算密钥evk。

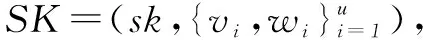
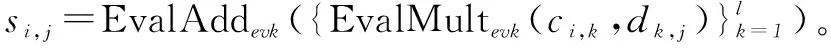
d) Verify(S，SK)：客户端首先对S中的每个元素进行解密：hi，j=Decsk(si，j)。对每个i∈[1，u]，计算Hvi=wi是否成立。若全部成立，则接受此次的计算结果，反之拒绝。

3 协议分析

上述协议的正确性和隐私性是显然的，而其可验证性基于如下引理：

引理1[4]：给定两个不同的矩阵A，A′∈Rl×l(其中R为有限交换环)，随机选取v∈Rl，我们有Pr(Av=A′v)≤1/|R|。

由此可见，服务器以一个错误结果成功欺骗客户的概率为|R|-p。又因为u=poly(n)，该概率对安全参数n而言是可忽略的，可验证性成立。最后，本协议的各项性质以及与现有的一些相关协议的比较如表1所示。

表1 文中协议与其他现有同类协议对比

表1中梳理了文中提到的协议的各项性质。为了简洁起见，表1中的计算开销仅包括了模内加法运算(ta)、乘法运算(tm)以及指数运算(te)所需的时间开销。由此可见，本文中的协议无需使用相较昂贵的指数运算，其效率较大部分同类协议高；由于其基于的困难性问题为RLWE问题，也达到了较高的安全性。

4 结语

本文梳理总结了近年来用于矩阵乘的可验证计算协议，并在现有的同态算法以及验证框架基础上构造了一种高效的并带有隐私保护的用于矩阵乘的可验证计算协议。相比于现有的方案，本方案具有抵抗量子分析的隐私性以及较高的效率。下一步，将针对进一步提高加密以及验证效率和更复杂的应用场景展开研究。