景永强 彭妙娟

摘要：为提高断裂弹性动力学问题数值计算的精度，避免出现病态或奇异方程组，基于改进的移动最小二乘法建立三维弹性动力学问题的积分弱形式，采用罚函数法施加位移边界条件，引入隐式时间积分并且结合三维断裂力学的形函数考虑裂纹尖端的奇异性，探究将改进的无单元Galerkin（improved element-free Galerkin， IEFG）法用于断裂弹性动力学问题的数值计算。通过悬臂梁、柱和矩形板等3个算例，討论节点分布、影响域比例参数、罚因子和时间步长等参数对计算精度的影响，证明IEFG法用于求解三维断裂弹性动力学问题的正确性和有效性。

关键词：

弹性动力学; 断裂力学; 裂纹; 改进的移动最小二乘法; 形函数; 隐式时间积分

中图分类号：O241.82; TB115.1

文献标志码：B

Improved element-free Galerkin method for

three-dimensional fracture elasto-dynamics

JING Yongqiang， PENG Miaojuan

（Department of Civil Engineering， School of Mechanics and Engineering Science， Shanghai University， Shanghai 200444， China）

Abstract：

To improve the accuracy of the numerical calculation of fracture elasto-dynamics， and to avoid the ill conditioned or singular equations， the improved element-free Galerkin（IEFG） method is applied to the numerical calculation of fracture elasto-dynamics. Based on the improved moving least square method， the integral weak form of the three-dimensional elasto-dynamics problem is established. The penalty function method is used to set the displacement boundary conditions. The singularity of crack tip is considered by introducing the implicit time integration and the shape function of three-dimensional fracture mechanics. Three examples（include the cantilever beam， the column and the square plate） are selected to analyze the influence of computing parameters（include the node distribution， the influence domain scale parameter， the penalty factor and the time step） on the calculation accuracy. It is proved that the IEFG method is correct and effective for solving three-dimensional fracture elasto-dynamics problems.

Key words：

elasto-dynamics; fracture mechanics; crack; improved moving least square method; shape function; implicit time integration

0 引 言

断裂弹性动力学问题是断裂力学与弹性动力学耦合的问题，传统的解析方法难以求解，目前可采用的数值方法主要有有限元法和无单元法等。采用有限元法求解断裂力学问题时，在裂纹的发生扩展过程中需要重新划分网格，计算精度较低。无单元法无须划分网格，只需要节点信息。对于含有裂纹的构件，为提高计算精度，无单元法可以在裂纹处布置加密节点，避免对网格和单元依赖的问题，在求解断裂弹性动力学问题时具有一定的优势。

BELYTSCHKO等[1]采用无单元Galerkin法研究三维几何和材料非线性的动力学问题。CHEN等[2]采用无单元Galerkin法研究材料高速撞击发生弹塑性大变形的问题。LEE等[3]采用无单元Galerkin法对裂纹的奇点进行不连续性建模，提出一种改进的裂纹分析技术。RAO等[4]提出一种改进的无单元法，用于均匀、等向、非线性弹性二维固体裂缝的断裂分析。

无单元Galerkin法利用移动最小二乘法构造试函数，因此具有较高的计算精度，但计算过程中形成的方程组有时是病态的或奇异的。陈美娟等[5]提出改进的移动最小二乘法，基函数采用正交函数，可有效避免病态或奇异方程组的产生，不需要求解逆矩阵，可提高计算效率。ZHANG等[6]提出改进的无单元Galerkin（improved element-free Galerkin， IEFG）法，并用于解决三维势问题、波动方程、断裂力学和瞬态热传导问题。CHENG等[7]提出针对三维弹性力学、弹性动力学等问题的IEFG法。SUN等[8]研究共平面方形裂纹，对等向弹性体中二维和三维共平面方形裂纹的相互作用进行数值模拟。PENG等[9]在改进的移动最小二乘法的基础上，提出针对三维黏弹性问题的IEFG法。ZHANG等[10]基于改进的移动最小二乘法，在裂缝尖端使用基函数，提出一种可以解决二维断裂问题的IEFG法。魏庆节等[11]基于改进的移动最小二乘法建立三维弹性动力学问题的形函数，结合三维弹性动力学的Galerkin积分弱形式，采用罚函数法施加位移边界条件，引入隐式时间积分，并提出三维弹性动力学的IEFG法。蔡小杰等[12]基于改进的移动最小二乘法，提出针对弹塑性大变形问题的IEFG法，讨论权函数、影响域比例参数、罚因子、节点数和迭代步数等参数对计算精度的影响。邹诗莹等[13]在IEFG法的基础上，将能反映裂纹尖端附近应力奇异性的特征项引入改进的移动最小二乘法的基函数中，将断裂力学与IEFG法相结合，用于研究线弹性断裂力学问题，并对含反射裂缝的机场复合路面层状体系结构进行数值分析。

刘学聪等[14]基于扩展有限元法提出一种新的裂纹尖端加强函数，组合传统的函数基，继承传统附加函数的特性，使节点的奇异附加自由度减少为2个，可减小总矩阵的规模，提高计算效率。石路杨等[15]引入裂纹交叉汇合加强函数，分析多裂纹的交叉汇合过程，在裂纹附近区域使用广义形函数，并引入线性递增函数消除混合单元，建立求解多裂纹扩展的扩展有限元法，可有效提高裂纹附近的分析精度。杨永涛等[16]基于包含裂纹尖端增强函数的数值流形方法，采用Newmark隐式动力学算法进行时间积分，重点研究动力载荷作用下裂纹动态应力强度因子的求解方法。张洪武等[17]基于精细网格的传统有限元分析方法，针对非均质饱和多孔介质弹塑性动力问题，提出一种广义耦合扩展多尺度有限元法。

分析以上研究发现，在求解断裂力学问题时IEFG法优于有限元法。目前，IEFG法在三维弹性力学、弹性动力学、弹塑性大变形、黏弹性和线弹性断裂力学等方面的研究较多，针对断裂弹性动力学问题，IEFG法的研究很少。本文基于改进的移动最小二乘法，建立三维弹性动力学问题的积分弱形式，采用罚函数法施加位移边界条件，引入隐式时间积分，并且结合三维断裂力学的形函数考虑裂纹尖端的奇异性。采用改进的移动最小二乘法可避免病态或奇异方程组，保证IEFG法的计算精度。三维断裂弹性动力学IEFG法不仅要考虑三维弹性动力学中加速度和阻尼的影响，还要考虑断裂力学裂纹尖端的奇异性。本文结合改进的移动最小二乘法、弹性动力学和断裂力学的无单元Galerkin法，建立三维断裂弹性动力学的IEFG法的离散方程，并推导相应的计算公式，采用悬臂梁、柱和方形板等3个数值算例证明三维断裂弹性动力学IEFG法的正确性和有效性。

1 三维断裂弹性动力学基本方程

三维线弹性动力学的控制方程为

LTσ+b=ρu··+μu·， x∈Ω

（1）

式中：L为微分算子矩阵;σ为应力向量;b为外力向量;ρ为质量密度;u为位移向量;μ为阻尼系数;x为点的集合。L、σ、b和u分别定义为

L=x1000x2000x3x2x10x30x10x3x2

（2）

σ=[σ11 σ22 σ33 σ12 σ13 σ23]T

（3）

b=[b1（t） b2（t） b3（t）]T

（4）

u=[u1（t） u2（t） u3（t）]T

（5）

式中：xi（i=1，2，3）為点x紧支域内的点;σij（i，j=1，2，3）为不同方向的应力;t为时间。

三维线弹性动力学控制方程的边界条件为

ui-i=0， i=1，2，3， x∈Γu

（6）

njσij-ti=0， i，j=1，2，3， x∈Γt

（7）

式中：i为边界Γu上的已知位移;nj为边界Γt的外法线方向的余弦;ti为边界Γt上的已知面力。Γu∪Γt=Γ，Γ为求解域Ω的边界。

三维线弹性动力学控制方程的初始条件为

ui（x，t0）=ui0（x）， x∈Ω（8）

u·i（x，t0）=vi0（x）， x∈Ω （9）

式中：vi0和ui0分别为点x的初始速度和初始位移;t0为初始时间。

三维线弹性动力学控制方程的本构方程为

σ=Dε

（10）

其中：

ε=Lu

（11）

D=E（1-v）（1+v）（1-2v）1v1-vv1-v000v1-v0v1-v000v1-vv1-v00000001-2v2（1-v）0000001-2v2（1-v）0000001-2v2（1-v）

（12）

式（11）即为三维线弹性动力学控制方程的几何方程。

为得到弹性动力学的Galerkin弱形式，采用罚函数法施加位移边界条件，即

∫ΩδuT·ρu··dΩ+ ∫ΩδuT·μu·dΩ+∫ΩδεT·σdΩ+

∫ΓtδuT·bdΩ-∫ΓtδuT·tdΩ+

α∫ΓtδuT·S（u-）dΓ=0

（13）

式中：α为罚因子;

=[1 2 3]T （14）

t=[t1 t2 t3]T（15）

将式（10）和（11）代入式（13），计算得到罚函数法的可行域为

S=S1000S2000S3

（16）

∫ΩδuT·ρu··dΩ+∫ΩδuT·μu·dΩ+∫Ωδ（Lu）T·（Lu）dΩ+∫ΩδuT·bdΩ-∫ΓtδuT·tdΩ+α∫ΓtδuT·S（u-）dΓ=0（17）

当x1、x2、x3有位移约束时，对应的S1、S2、S3等于1，否则等于0。

2 三维断裂弹性动力学的IEFG法

利用改进的移动最小二乘法建立逼近函数。由文献[13]中裂纹尖端的应力场表达式可知，裂纹尖端附近的位移与特征项r（r为点x到裂纹尖端的距离）成正比，应力具有1/r阶奇异性。为有效计算裂纹尖端场的应力数值解，在基函数中加入扩展函数项，由改进的移动最小二乘法得到形函数。基于三维弹性动力学IEFG法，在基函数中加入文献[13]中裂纹尖端位移场表达式中的重要项和重要的梯度项，使IEFG法的计算结果更精确。

结合文献[13]得到三维断裂力学IEFG法的试函数为

pT（x）=1 x1 x2 x3 rcos θ2 rsin θ2

rsin θ2sin θ rcos θ2sin θ

（18）

PI（x）=[w（x-x1）p（x1） w（x-x2）p（x2） …

w（x-xn）p（xn）]

（19）

式中：θ为裂纹的扩展角;n为影响域覆盖点x的节点数;xn为点x的紧支域内的节点;w（x-xn）为具有紧支集特性的权函数。

类似文献[11]中移动最小二乘法的形函数推导，可得到三维断裂弹性动力学的逼近函数为

uα，h（x）=nI=1pT（x）A-1（x）PI（x）uα（xI）

（20）

式中：A-1（x）为由pi构成的对角矩阵。

三维断裂弹性动力学的形函数为

ΦI（x）=pT（x）A-1（x）PI（x）

（21）

将式（21）代入式（20），可得

uα，h（x）=nI=1ΦI（x）uα（xI）

（22）

采用局部基函数扩展法，在基函数中加入特征项r，即

pT（x）=[1 x1 x2 x3 r]

（23）

将求解域离散为有限个节点，节点总数为M。利用改进的移动最小二乘法建立逼近函数，可以得到位移的逼近函数为

ui（x，t）=nI=1ΦI（x）uI（xI，t）， i=1，2，3

（24）

即 u（x，t）=nI=1ΦI（x）uI

（25）

将式（24）和（25）代入式（17）可得

∫ΩδnI=1ΦIuITρnJ=1ΦJu··JdΩ+∫ΩδnI=1ΦIuITμnJ=1ΦJu·JdΩ+∫ΩδnI=1LuITDnJ=1ΦJLuJdΩ-

∫ΩδnI=1ΦIuITbdΩ-∫ΓtδnI=1ΦIuITtdΓ+∫ΓtδnI=1ΦIuITSnJ=1ΦJu··JdΓ+∫ΓtδnI=1ΦIuITSu··dΓ=0

（26）

对式（26）进行积分运算，可以得到三维断裂弹性动力学的离散方程为

MU··（t）+CU·（t）+（K+Kα）U（t）=F（t）+Fα

（27）

其中：

M=（Mij），Mij=∫ΩΦiρΦjdΩ， i，j=1，2，…，M

（28）

U=[uT1（t） uT2（t） … uTM（t）]T

（29）

C=（Cij），Cij=∫ΩΦiμΦjdΩ， i，j=1，2，…，M

（30）

K=（Kij），Kij=∫ΩBTiDBjdΩ， i，j=1，2，…，M

（31）

Bi=Φi，2000Φi，2000Φi，3Φi，2Φi，10Φi，30Φi，10Φi，3Φi，2， i=1，2，…，M

（32）

Kα=（Kij，α），Kij，α=α∫ΓtΦiSΦjdΓ，

i，j=1，2，…，M

（33）

F=（Fij），Fij=∫ΩΦibdΩ+∫ΓtΦjtdΓ，

i，j=1，2，…，M

（34）

Fα=（Fi，α），Fi，α=α∫ΓtΦiSdΓ，i=1，2，…，M

（35）

3 隱式时间积分

隐式时间积分方法可实现求解目标在大时间步长内的无条件稳定，被广泛应用于各种动力学问题中。本文采用Newmark-β法对运动方程进行时间离散。假设时刻t的时间域[0，T]被离散为n个时间步（即Δt=T/n），位移Ut及其对应导数U·t、U··t的值均已知，对U·t+Δt和U··t+Δt进行二阶Taylor展开可得

Ut+Δt=Ut+ΔtU·t+12（1-β2）Δt2U··t+12β2Δt2U··t+Δt

（36）

U·t+Δt=U·t+（1-β1）ΔtU··t+β1ΔtU··t+Δt

（37）

U··t+Δt=2β2Δt2（Ut+Δt-Ut）-2β2ΔtU·t-1β2-1U··t

（38）

式中：β1和β2均为Newmark参数，分别取β1=3/2，β2=8/5。

令α1=2β2Δt2、α2=2β2Δt、α3=1β2-1，可得

U··t+Δt=α1（Ut+Δt-Ut）-α2U·t-α3U··t

（39）

将式（39）代入式（37）可得

U·t+Δt=β1α2（Ut+Δt-Ut）+1-2β1β2U·t+

1-β1β2ΔtU··t

（40）

根据隐式时间积分方法，式（27）可写成

MU··t+Δt+CU·t+Δt+（K+Kα）Ut+Δt=Ft+Δt+Fα

（41）

将式（39）和（40）代入式（41）可得

（α1M+β1α2C+K+Kα）Ut+Δt=

Ft+Δt+Fα+M（α1Ut+α2U·t+α3U··t）+

Cβ1α1Ut+2β1β2-1U·t+β1β2-1ΔtU··t

（42）

4 数值算例

选择悬臂梁、柱和矩形板等3个算例，验证IEFG法的正确性和有效性。3个算例的权函数均为三次样条权函数，将计算结果与Abaqus软件有限元法计算结果进行比较。

为分析IEFG法的精确度，定义均方差为

eI=1NNi=1（uIEFG，i-uAbaqus，i）

（43）

式中：uIEFG，i为IEFG法的计算结果;uAbaqus，i为Abaqus的计算结果;N为节点数。

为讨论Abaqus解的准确性和收敛性，定义方差

eA=1NNk=1（uJ，k-IJ，k）2+（uI，k-IJ，k）2

（44）

式中：uI，k和uJ，k分别为节点分布I和J下第k个节点的数值解;IJ，k为uI，k和uJ，k的平均值。

4.1 受突加线性分布载荷作用的悬臂梁

选取某典型悬臂梁，上、下表面自由，一端固定，另一端受突加线性分布载荷作用，见图1，其中a=120 mm、b=120 mm、c=360 mm、r=30 mm。材料参数分别取ρ=2 405 kg/m3、E=20.69 GPa、ν=0.15，g取9.8 m/s2。在x3=-60 mm和x3=60 mm处施加突加载荷P=1×103 N。

利用有限元软件Abaqus对该算例进行计算，有限元网格采用20节点二次六面体单元C3D20R，分别取9×9×15、15×15×31、15×15×51、17×17×65和33×33×81等5种节点分布，悬臂梁自由端Q点（x1=360 mm、x2=-60 mm）位移数值解的方差见图2。由此可知，随着网格的细化，方差逐渐趋于0，说明Abaqus的数值解收敛。与IEFG方法的数值解进行对比时选择节点分布为33×33×81，Abaqus中悬臂梁的网格划分结果见图3。

根据三维断裂弹性动力学IEFG法的离散方程，采用与Abaqus计算时同样的节点分布，利用MATLAB对悬臂梁Q点位移进行数值计算，不同節点分布时悬臂梁位移的均方差结果见图4。由此可知，随着节点数增加，IEFG法的均方差逐渐减小，计算精度逐渐提高。

影响域比例参数dmax在1.5～3.5范围内取不同值时，悬臂梁位移均方差的变化见图5。由此可知，当dmax在2.5～3.0范围内时，悬臂梁位移的均方差较小，说明此时数值解的计算精度较高。

给定影响域比例参数dmax，取不同时间步长Δt，计算悬臂梁位移的均方差，结果见图6。由此可知，随着时间步长的增大，均方差逐渐增大。当时间步长为1.0×10-6 s时均方差较小，说明此时数值解的计算精度较高。

给定影响域比例参数dmax和时间步长，取不同罚因子α，计算悬臂梁位移的均方差，结果见图7。由此可知，随着罚因子的增大，均方差呈类似抛物线分布。当罚因子α=2.5×1015时均方差较小，说明此时数值解的计算精度较高。

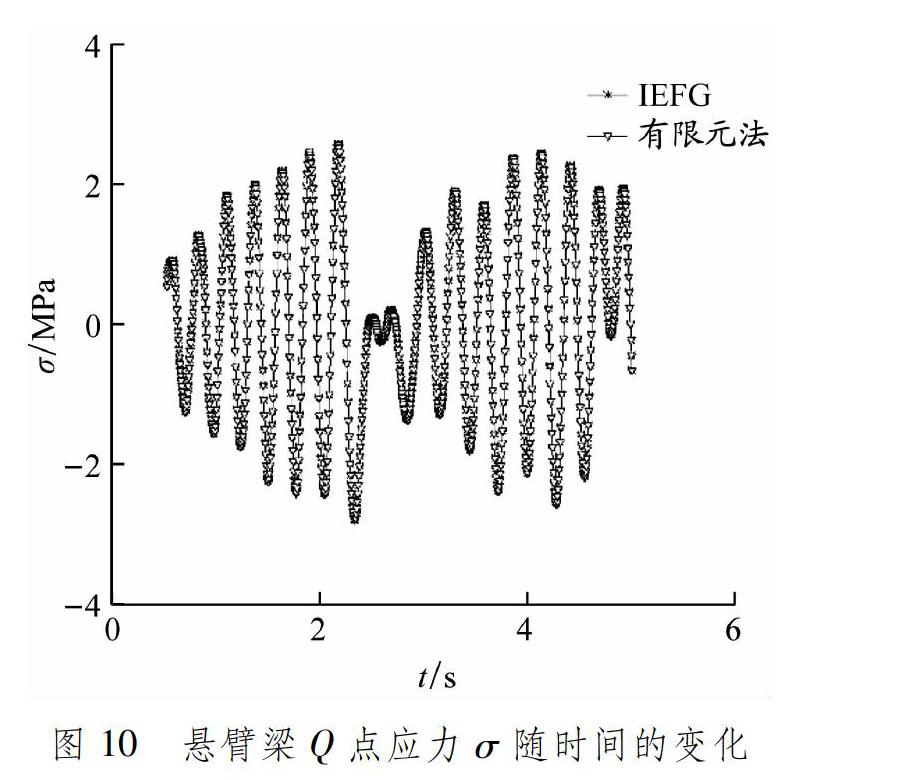
取dmax=2.7、Δt=1.0×10-6 s、α=2.5×1015，Abaqus中节点分布取33×33×81，计算图1中自由端Q点的位移u1、u3和应力σ随时间的变化，见图8～10。由此可知，IEFG法与有限元法的计算结果吻合，证明IEFG法解决三维断裂弹性动力问题的正确性和有效性。

4.2 受突加载荷作用的柱

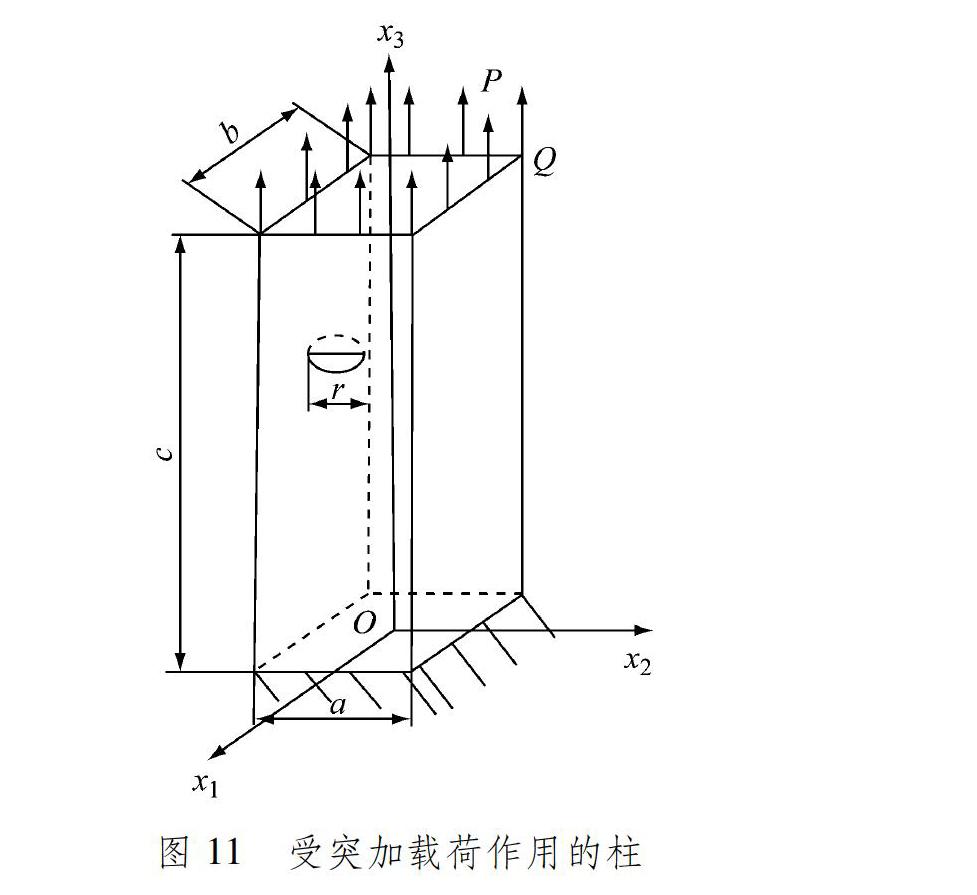
选取单边带有半圆型裂纹的柱形试件，裂纹位于试件中部，裂纹半径r=5 cm，试件下端固定，上端施加单向突加载荷作用，见图11。突加载荷P=20 kPa，材料和几何参数取E=210 GPa、ν=0.35、a=30 cm、b=30 cm、c=120 cm。

利用Abaqus对柱位移进行计算，有限元网格采用20节点二次六面体单元C3D20R，取9×9×17、9×9×31、17×17×64、21×21×71和41×41×81等5种节点分布，计算得到Q点（x1=-15 cm、x3=120 cm）位移的方差，见图12。随着节点数增加，Abaqus数值解的方差趋于0，说明Abaqus的数值解收敛。与IEFG法的数值解进行对比时选择节点分布为41×41×81，Abaqus中柱的网格划分结果见图13。

根据三维断裂弹性动力学IEFG法的离散方程，取dmax=2.8、Δt=1.0×10-6 s、α=2.5×1015，利用MATLAB对柱位移进行数值计算，图11中Q点的位移u1、u3和应力σ随时间的变化见图14～16。由此可知，IEFG法与有限元法计算结果吻合，证明IEFG法的正确性和有效性。

4.3 受突加载荷作用的矩形板

选取带有半圆型裂纹的矩形板，下表面固定，上表面受突加均布载荷作用，见图17，其中r=0.03 m、a=3 m、b=3 m、c=1 m。矩形板的弹性模量E=210 GPa、泊松比ν=0.15，突加载荷P=100 MPa。

利用Abaqus计算矩形板位移，有限元网格采用20节点二次六面体单元C3D20R，取21×21×11，31×31×21，41×41×31，61×61×41和81×81×61等5种节点分布，图17中矩形板Q点（x1=1.5 m、x3=1.0 m）位移的方差见图18。随着节点数增加，方差趋于0，说明Abaqus的数值解收敛。与IEFG法数值解对比时选择节点分布为81×81×61，Abaqus中矩形板的网格划分结果见图19。

根据三维断裂弹性动力学IEFG法的离散方程，利用MATLAB对矩形板位移进行数值计算，取dmax=2.8、Δt=1.0×10-6 s、α=2.5×1015，图17中Q点的位移u1、u3和应力σ随时间的变化见图20～22。IEFG法与有限元法计算结果吻合，证明IEFG法的正确性和有效性。

5 结束语

基于改进的移动最小二乘法，提出三维断裂弹性动力学的IEFG法。通过悬臂梁、柱和矩形板3个算例，对比分析节点分布、影响域比例参数、罚因子和时间步长等参数对计算精度的影响。本文提出的三维断裂力学的IEFG法计算结果与有限元法计算结果吻合，证明该方法的正确性和有效性。

参考文献：

[1] BELYTSCHKO T， KRYSL P， KRONGAUZ Y. A three-dimensional explicit element-free Galerkin method[J]. International Journal for Numerical Methods in Fluids， 1997， 24（12）： 1253-1270. DOI： 10.1002/（SICI）1097-0363（199706）24：12〈1253：：AID-FLD558〉3.0.CO;2-Z.

[2] CHEN Y P， ESKANDARIAN A， OSKARD M， et al. Meshless analysis of high-speed impact[J]. Theoretical and Applied Fracture Mechanics， 2005， 44（3）： 201-207. DOI： 10.1016/j.tafmec.2005.09.007.

[3] LEE S H， YOON Y C. An improved crack analysis technique by element-free Galerkin method with auxiliary supports[J]. International Journal for Numerical Methods in Engineering， 2003， 56（9）： 1291-1314. DOI： 10.1002/nme.611.

[4] RAO B N， RAHMAN S. An enriched meshless method for non-linear fracture mechanics[J]. International Journal for Numerical Methods in Engineering， 2004， 59（2）： 197-223. DOI： 10.1002/nme.868.

[5] 陈美娟， 程玉民. 改进的移动最小二乘法[J]. 力学季刊， 2003， 24（2）： 266-272. DOI： 10.3969/j.issn.0254-0053.2003.02.019.

[6] ZHANG Z， WANG J F， CHENG Y M， et al. Improved element-free Galerkin method for three-dimensional transient heat conduction problems[J]. Science China Physics， Mechanics and Astronomy， 2013， 56： 1568-1580. DOI： 10.1007/s11433-013-5135-0.

[7] CHENG Y M， PENG M J. Boundary element-free method for elastodynamics[J]. Science in China Series G： Physics and Astronomy， 2005， 48： 641-657. DOI： 10.1360/142004-25.

[8] SUN Y Z， LIEW K M. Analyzing interaction between coplanar square cracks using an efficient boundary element-free method[J]. International Journal for Numerical Methods in Engineering， 2012， 91（11）： 1184-1198. DOI： 10.1002/nme.4309.

[9] PENG M J， LI R X， CHENG Y M. Analyzing three-dimensional viscoelasticity problems via improved element-free Galerkin（IEFG） method[J]. Engineering Analysis with Boundary Elements， 2014， 40： 104-113. DOI： 10.1016/j.enganabound.2013.11.018.

[10] ZHANG Z， LIEW K M， CHENG Y M， et al. Analyzing 2D fracture problems with improved element-free Galerkin method[J]. Engineering Analysis with Boundary Elements， 2008， 32（3）： 241-250. DOI： 10.1016/j.enganabound.2007.08.012.

[11] 魏慶节， 彭妙娟. 三维弹性动力学的改进的无单元Galerkin方法[J]. 应用力学学报， 2019， 36（1）： 22-27.

[12] 蔡小杰， 彭妙娟， 程玉民. 弹塑性大变形问题的改进的无单元Galerkin方法[J]. 中国科学， 2018， 48（2）： 53-62. DOI： 10.1360/SSPMA2017-00231.

[13] 邹诗莹， 席伟成， 彭妙娟， 等. 运用改进的无单元Galerkin方法分析机场道面断裂力学问题[J]. 物理学报， 2017， 66（12）： 36-44. DOI： 10.7498/aps.66.120204.

[14] 刘学聪， 章青， 夏晓舟. 一种新型裂尖加强函数的显式动态扩展有限元法[J]. 工程力学， 2017， 34（10）： 10-18. DOI： 10.6052/j.issn.1000-4750.2016.05.0399.

[15] 石路杨， 余天堂. 多裂纹扩展的扩展有限元法分析[J]. 岩土力学， 2014， 35（1）： 263-272. DOI： 10.16285/j.rsm.2014.01.001.

[16] 杨永涛， 徐栋栋， 郑宏. 动载下裂纹应力强度因子计算的数值流形元法[J]. 力学学报， 2014， 46（5）： 730-738. DOI： 10.6052/0459-1879-14-024.

[17] 张洪武， 卢梦凯， 郑勇刚. 非均质饱和多孔介质弹塑性动力分析的广义耦合扩展多尺度有限元法[J].计算力学学报， 2016， 33（4）： 454-461. DOI： 10.7511/jslx201604005.

（编辑 武晓英）