王乐洋，陈 涛，邹传义,2

1. 东华理工大学测绘工程学院，江西 南昌 330013； 2. 武汉大学测绘学院，湖北 武汉 430079

在大地测量数据处理领域中，若观测误差随观测量的大小或物理信号的强弱而变化，则该类误差为乘性误差[1]。例如，现代观测手段中的合成孔径雷达SAR观测值的随机误差表现为乘性误差[2-3]，光电测距EDM(electronic distance measurement)和全球定位系统GPS的观测误差表现为乘性误差或者加乘性混合误差[4-5]。目前，在大地测量领域中关于乘性误差模型参数估计和精度评定的研究成果相对较少[6-9]，且其中尚无文献针对乘性误差模型中存在的病态问题进行研究，因此如何对病态乘性误差模型进行参数估计和精度评定是值得研究的问题。

病态问题广泛存在于测绘数据处理中，模型的病态性会造成参数解的不稳定，甚至严重偏离真值[10]。已有的总体最小二乘病态问题[11]、大地测量反演的病态问题[12]和控制网平差的病态问题[13]等都是基于加性误差模型建立的，而对于乘性误差模型的病态问题尚未发现研究成果。乘性误差模型的最小二乘解法最早由文献[6]提出，文献[7]在文献[6]的基础上，总结了乘性误差模型的最小二乘、加权最小二乘和偏差改正加权最小二乘方法，并推导了参数估计的精度评定公式。若直接采用文献[7]中的3种方法处理病态乘性误差模型，而不考虑系数矩阵的病态性，会使参数估值产生偏差且不稳定。文献[4]为避免系数矩阵病态，将模拟点集中在数字地面模型(digital terrain model,DTM)中的峰值处，其他的点均匀分布，这仅可用来处理模拟数据，无法适用于真实的观测数据。系数矩阵病态会使得系数矩阵的列向量之间存在复共线性，进而引起法方程条件数过大，导致解不稳定[10]。目前，处理病态问题的方法主要有Tikhonov正则化法[14-16]和虚拟观测值解法[17]等。正则化参数的确定方法，主要有广义交叉核实法[18]、岭迹法[19]和L曲线法[20-22]等。广义交叉核实法难以获得最优解，适用性弱；岭迹法虽然计算简单，但有一定的主观性；L曲线法适用性强，并且能获得较为合理的正则化参数，被广泛用于正则化参数的选取，可以很好地用于本文算法中正则化参数的选取。

经分析发现，使用加权最小二乘正则化法求解病态乘性误差模型时，参数估值是观测值的非线性函数，而观测值的协因数阵是参数估值的非线性函数，并且在逐步迭代的过程中参数的每一步估值都具有随机性，使得最终的参数估值与观测值为复杂的非线性关系，只能使用数值方法迭代求解，无法得到解析解。因此本文引入无需求导、无需获取非线性函数具体表达式的SUT法[23-24]对病态乘性误差模型进行精度评定。

综上所述，针对已有文献未考虑乘性误差模型的病态性，本文首先利用Tikhonov正则化方法导出病态乘性误差模型的加权最小二乘正则化解，其次通过SUT法对病态乘性误差模型进行精度评定；最后通过两个模拟数据算例和一个真实数据算例验证本文方法的适用性及优势。

1 乘性误差模型

给定一组带有乘性误差的观测值，相应的乘性误差模型可以表示为[7]

(1)

随机模型为

(2)

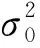
进一步可将式(1)改写为如下形式

y=f(β)⊙(1+εm)

(3)

式中，⊙表示哈达玛乘积符号。

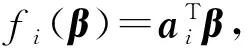
y=(Aβ)⊙(1+εm)

(4)

式中，A=[a1,a2,…,an]T；β=[β1,β2,…,βt]T。

由式(4)可知，在乘性误差模型中，观测值精度与系数矩阵和参数估值的乘积有关：信号Aβ越强，观测值y的误差越大；反之，信号Aβ越弱，误差越小。这明显区别于传统的加性误差模型，即观测值y的误差与系数矩阵和参数估值无关。目前，已有关于乘性误差模型的研究均不考虑系数矩阵A病态[7-8]，然而在大地测量实际数据处理中，系数矩阵A很容易出现病态，此时会引起法方程条件数过大，观测量微小的扰动将会引起参数较大的变化，导致解不稳定。例如，文献[25]针对SAR型噪声的特性采用乘性误差模型进行影像去噪，去噪效果达到70%～93%。此时，若系数矩阵A病态，会引起法方程条件数过大，导致解不稳定，进而影响影像去噪。因此需要针对病态乘性误差模型进行更深入的研究来丰富现代大地测量数据处理理论。

2 病态乘性误差模型参数估计的加权最小二乘正则化迭代解法及精度评定

2.1 病态乘性误差模型参数估计的加权最小二乘正则化解法

为了更方便地进行公式推导，将式(4)改写为如下形式

y-Aβ=(Aβ)⊙εm

(5)

令

(6)

(7)

根据最小二乘准则求解式(6)，得

(8)

β的最小二乘估值为

(9)

根据前文中的分析可知，当法方程N=ATA病态时，由式(9)求得的最小二乘解不可靠。因此，引入正则化因子α，构建如下病态乘性误差模型的正则化准则

(10)

对式(10)中的β求偏导，并令其为0，可得

(11)

将式(6)代入式(11)，可得病态乘性误差模型的加权最小二乘正则化解

(12)

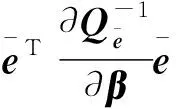
进而可以得到

(13)

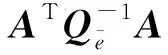
2.2 L曲线法基本原理

在确定本文病态乘性误差模型中的正则化参数时，由于观测值的协因数阵为参数估值的非线性函数，因此观测值的权阵也为参数估值的非线性函数，这使得正则化参数值产生动态变化。

2.3 病态乘性误差模型的精度评定

根据文献[8]，病态乘性误差模型的单位权方差估值可表示为

(14)

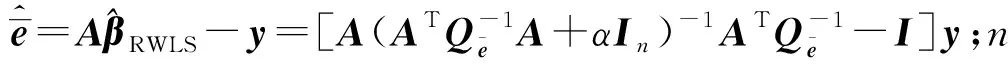
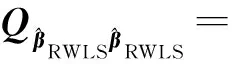
(15)

由偏差的定义[26]，对式(13)两边取期望，可得参数估值的偏差为

(16)

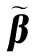
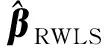
(17)

病态问题中，由于产生了偏差项，此时的均方误差不等于协方差不能作为一个良好的精度评判标准。虽然最小二乘估值是无偏，但已不是最优值[7]。根据均方误差的定义[30-31]，可知均方误差的表达式为

(18)

式中，等式右边第1部分表示参数估值协方差的迹；第2部分表示参数估值偏差平方的迹。

2.4 病态乘性误差模型参数估计的加权最小二乘正则化迭代解法

式(13)的迭代公式如下所示

(19)

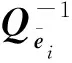
综上所述，本文将病态乘性误差模型的加权最小二乘正则化法迭代解法命名为算法1，具体步骤如下：

(1) 采用最小二乘法求得参数估值的初始值

(20)

(3) 求得正则化参数αi。

(4) 根据式(19)迭代求得病态乘性误差模型加权最小二乘正则化迭代解。

3 病态乘性误差模型精度评定的SUT法

由算法1可以看出，病态乘性误差模型的加权最小二乘正则化迭代解法中，每一步迭代参数估值都是观测值的函数，而观测值的协因数阵又是参数估值的函数，使得最终的参数估值与观测值为一个复杂的非线性函数。本文将这种非线性关系表示为[32-33]

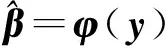
(21)

式中，φ(·)表示参数估值与观测值y之间的非线性函数。

第1步参数迭代估值可以表示为[32-33]

(22)

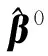
最终的参数估值表达式为[32-33]

(23)

式(23)表明，病态乘性误差模型的加权最小二乘正则化法的迭代过程使得参数估值和观测值之间的非线性关系非常复杂，且迭代的过程使参数的每一步的估值都具有随机性。为了避免复杂的公式运算，本文在病态乘性误差模型加权最小二乘正则化法中引入SUT采样法，旨在获得更精确的参数估值和精度信息。

本文将病态乘性误差模型精度评定的SUT法命名为算法2，步骤如下：

(1) 确定采样的先验统计均值和协方差阵。本文将观测值和对应的协方差阵作为采样的先验统计均值E(y)和协方差阵D(y)。

(2) 基于先验统计均值和协方差阵构造采样点集{χi}(i=0,1,2,…,2n)，生成2n+1个采样点

(24)

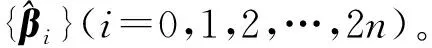
(4) 确定采样点集的权

(25)

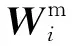
(5) 计算参数估值的均值和均方误差阵

(26)

(27)

(6) 计算单位权方差

(28)

本文首先对病态乘性误差模型加权最小二乘正则化迭代解法进行改化，将病态乘性误差模型中参数估值与观测值表示为嵌套函数的形式，然后引入无需求导、无需了解非线性函数构造的SUT法求解病态乘性误差模型中参数估值的均值、均方误差矩阵和单位权方差。

4 算例及分析

为了比较不同方法下参数估值和精度信息的差异，分别使用文献[7]中的未考虑病态性的三种方法即最小二乘法、加权最小二乘法和偏差改正加权最小二乘法，以及本文提出算法1和算法2进行解算。5种方案及对应的方法见表1。

表1 5种方案及对应的方法

4.1 算例1

为了验证本文公式推导以及算法的有效性，算例1根据文献[34]改编得到，通过利用GPS测量某一区域道路中心线地面点的高程，假定该区域道路中心线地面点高程真值与某一坐标原点的距离除以100符合以下函数模型

y=10+2x+x2+x3+0.5x4

(29)

式中，y为地面点高程的真值；x为高程点与某一坐标原点的距离除以100。

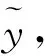
假设地面点高程真值被乘性误差干扰，其中乘性误差向量εm相互独立，且服从均值为0、标准差为0.1的正态分布，即εm～(0,0.12×I31)，相应的乘性误差模型的观测方程为

Y(x)=y(x)⊙(1+εm)

(30)

式中，Y(x)为受乘性误差干扰的地面高程点观测值向量；1为元素全为1的31维列向量；εm为31维乘性误差向量。

由式(30)得到一组地面高程点的数据模拟值见表2。为了说明高程点受乘性误差的影响程度，本文将地面高程点受乘性误差干扰前后的数据绘于图1中。

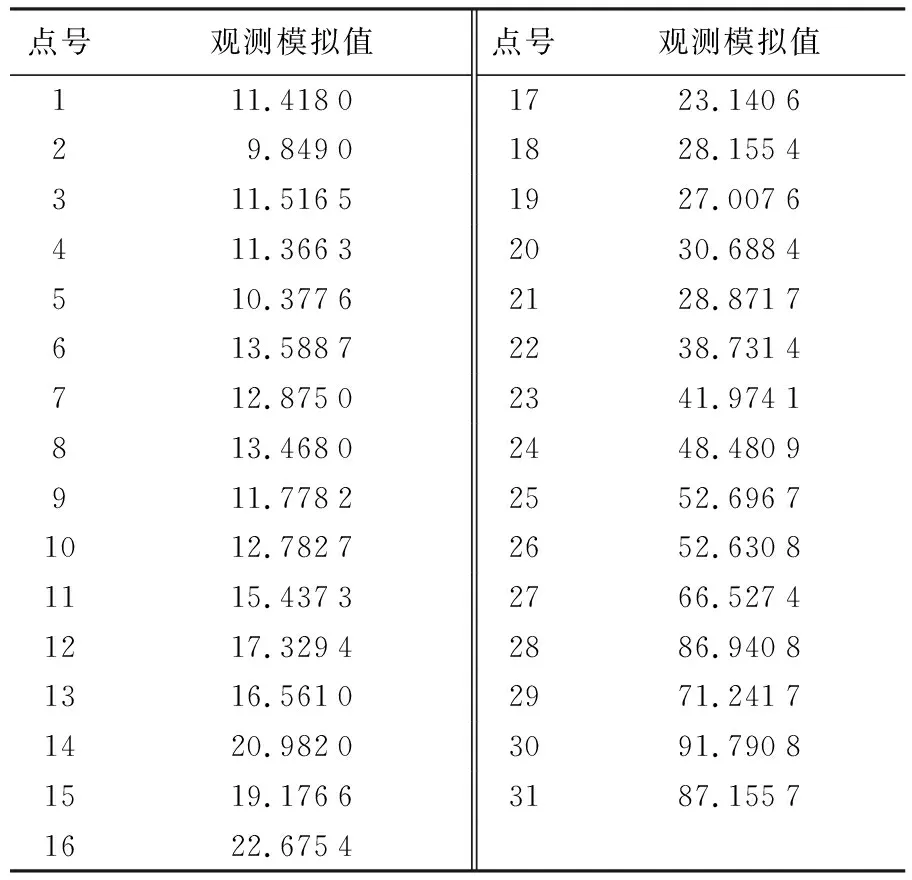
表2 数据模拟值

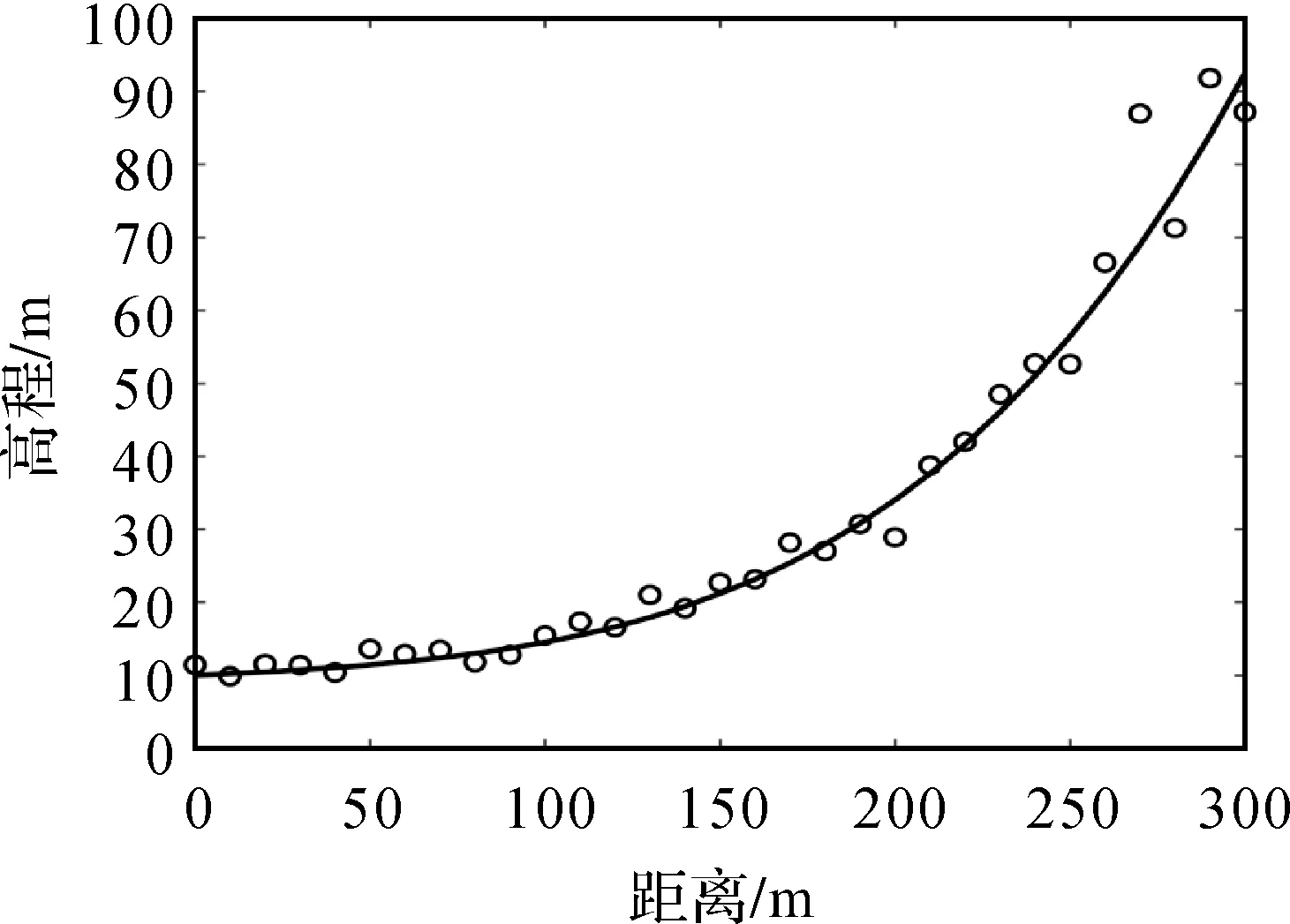
图1 地面高程点受乘性误差干扰前后分布Fig.1 GPS elevation points before and after disturbed by multiplicative error

本算例选取的单位权中误差σ0为0.3。使用表1中的5种方案计算，将参数真值、5种方案计算的参数估值、参数估值与真值的2范数及单位权中误差估值列于表3；5种方案计算的参数估值的均方根误差列于表4。

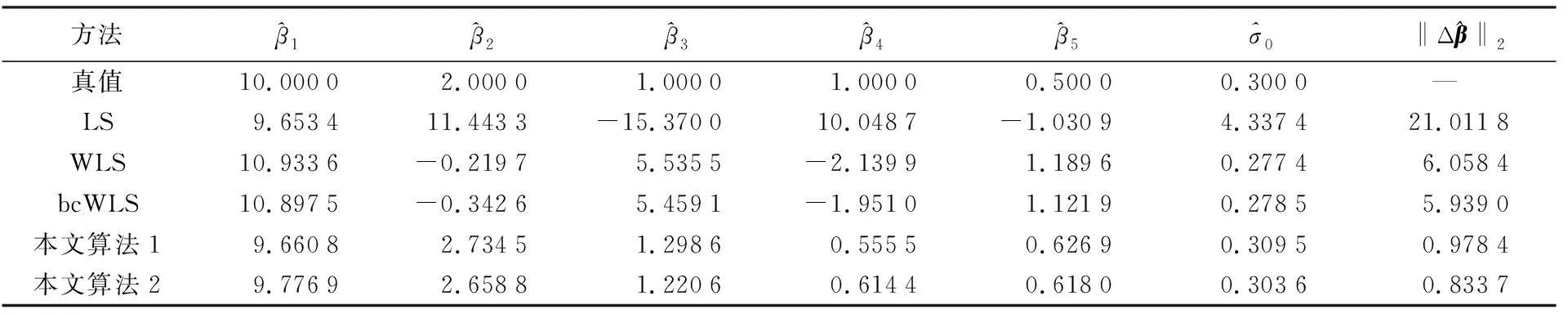
表3 参数估值、参数估值与真值之间的2范数和单位权中误差

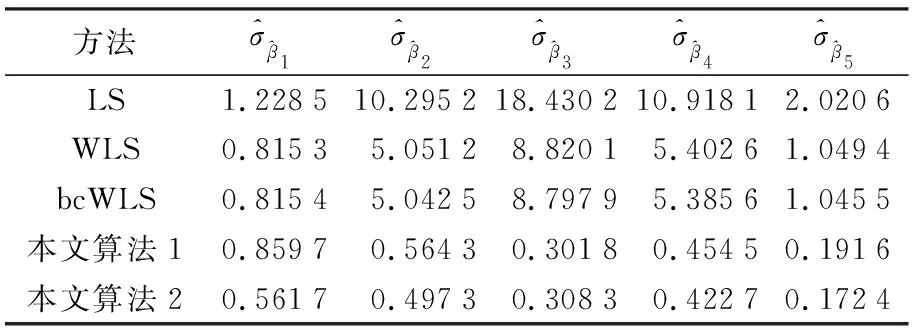
表4 参数估值的均方根误差

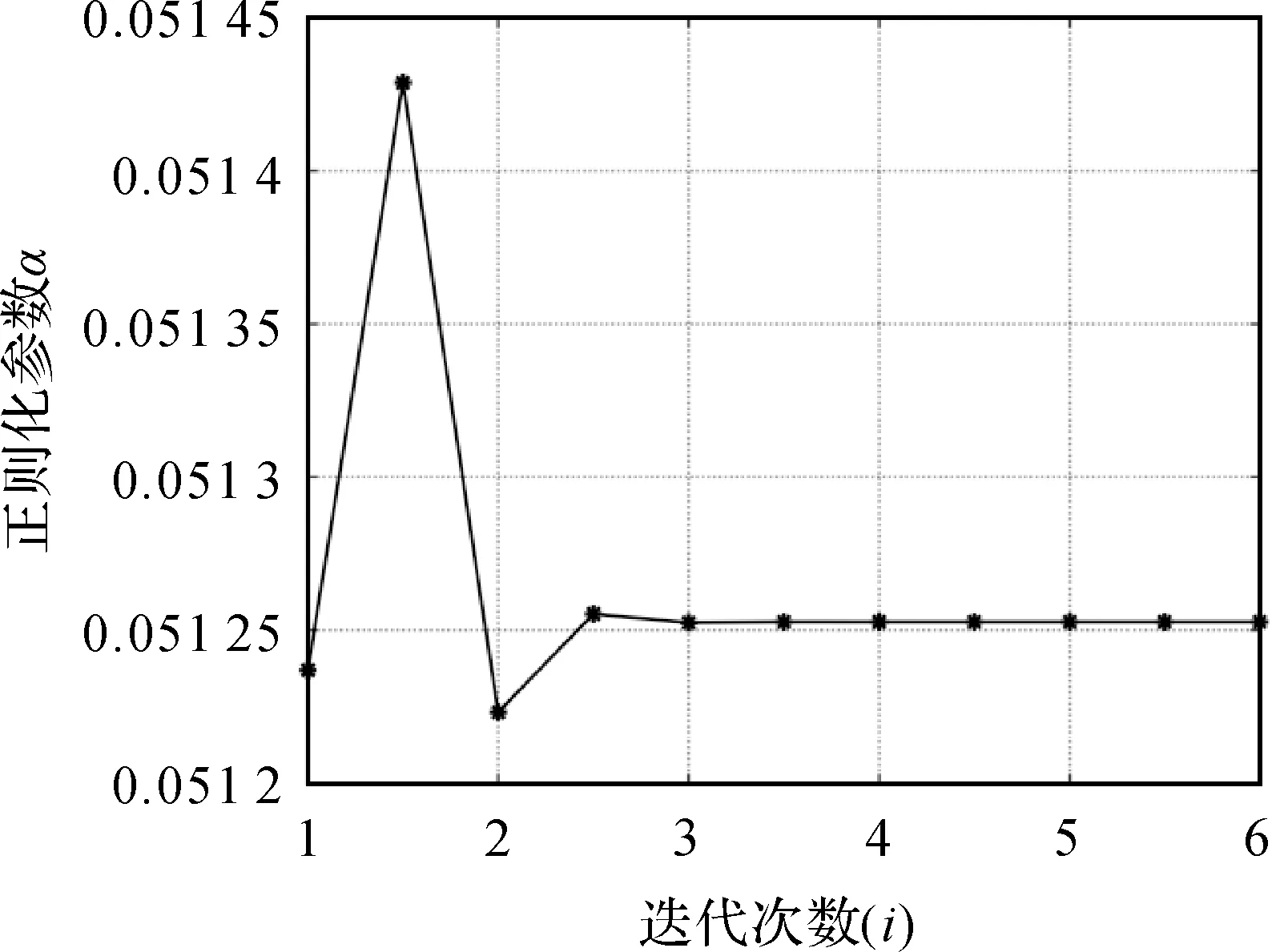
图2 正则化参数α随迭代次数的变化Fig.2 The regularization parameter with the number of iterations

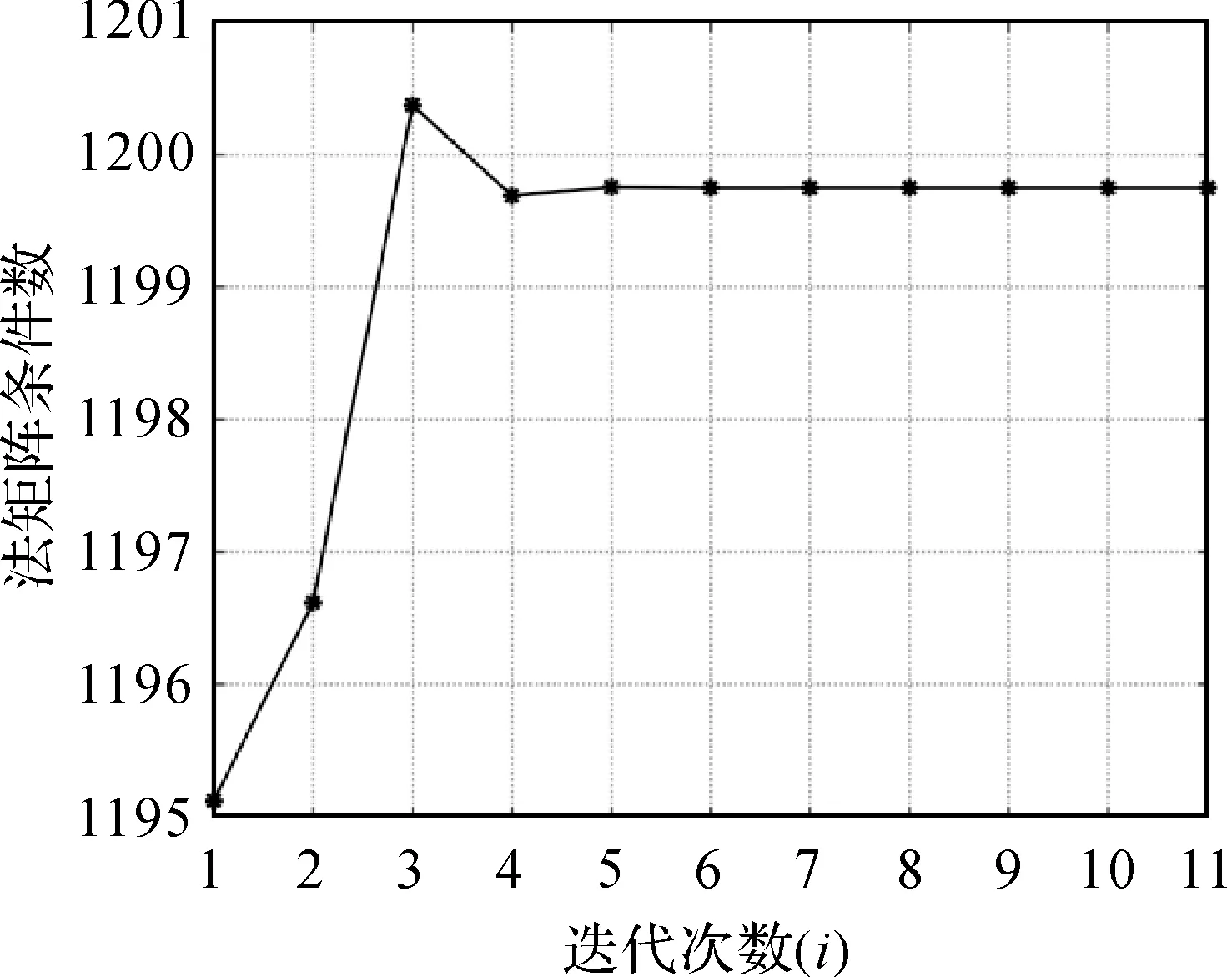
图3 法矩阵条件数随迭代次数的变化Fig.3 The condition number of the normal matrix with the number of iterations

由图1可知，由于地面高程点受到乘性误差干扰，导致点位产生了严重偏离。由表3中参数估值与真值的2范数可知，LS方法求得的2范数结果最大；WLS方法由于考虑了观测值的权得到的结果优于LS法，其2范数为6.058 4；bcWLS方法对WLS方法进行了偏差改正，2范数较WLS方法减小了0.119 4，为5.939 0，但由于未考虑模型的病态性，仍与真值偏离较大。本文算法1和算法2求得的2范数分别为0.978 4和0.833 7，参数估值更接近真值，说明本文算法对于降低病态性有一定的效果。其中，由于算法2考虑了正则化解法逐步迭代过程中每一步的随机性和非线性迭代的过程对参数估值的影响，求得的2范数较算法1减小了0.144 7，表明了本文使用SUT法的可行性。由表3中的单位权中误差可知，由于文献[7]中的方法未考虑模型的病态性，导致求得的单位权中误差偏离真值，而本文算法考虑了这些影响，求得的单位权中误差更接近真值，进一步表明了本文算法的优势。

4.2 算例2

算例2为一个DTM模型的算例，本文主要考虑模型为病态的情况，因此模拟一个病态DTM模型。文献[4]在模拟DTM模型时，为防止法矩阵病态情况出现，在模拟的DTM模型的每个峰值周围采样更多点，并使峰值点之间远离，虽然可以在一定程度上降低病态性，但仅可用来处理模拟数据，无法适用于真实的观测数据。本文依据文献[4]的思路，使用插值法来模拟DTM模型，插值法是模拟DTM模型的主要方法之一[35-36]，本文模拟的DTM模型由下面的插值函数生成

(31)

函数fi(x,y)(i=1,2,3,4)分别为如下

f1(x,y)=exp{-((x-22)2+(y-22)2)/500}

(32)

f2(x,y)=exp{-((x-28)2+(y-28)2)/500}

(33)

f3(x,y)=exp{-((x-25)2+(y-25)2)/500}

(34)

f4(x,y)=exp{-((x-20)2+(y-20)2)/500}

(35)

模拟的DTM模型如图4所示，相应的乘性误差模型的观测方程为

(36)

式中，h(x,y)为受乘性误差干扰的观测值向量；1为元素全为1的1681维列向量；εm为1681维乘性误差向量。

在本文中，假设误差向量εm相互独立、且服从均值为0，标准差为0.1的正态分布，即εm～(0,0.12×I1681)。为了说明DTM模型受乘性误差的影响程度，本文将不含误差的观测值绘于图4中，受乘性误差干扰的观测值绘于图5中。

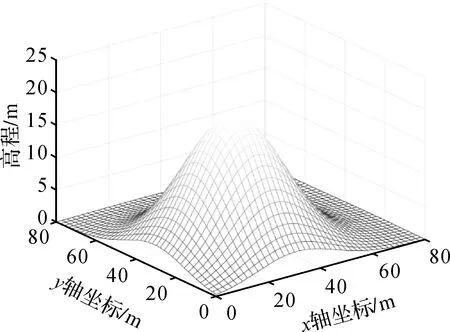
图4 模拟的DTM模型Fig.4 Simulated DTM model

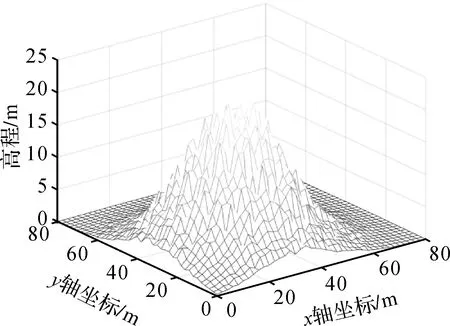
图5 受乘性误差干扰的DTM模型Fig.5 DTM model disturbed by multiplicative error

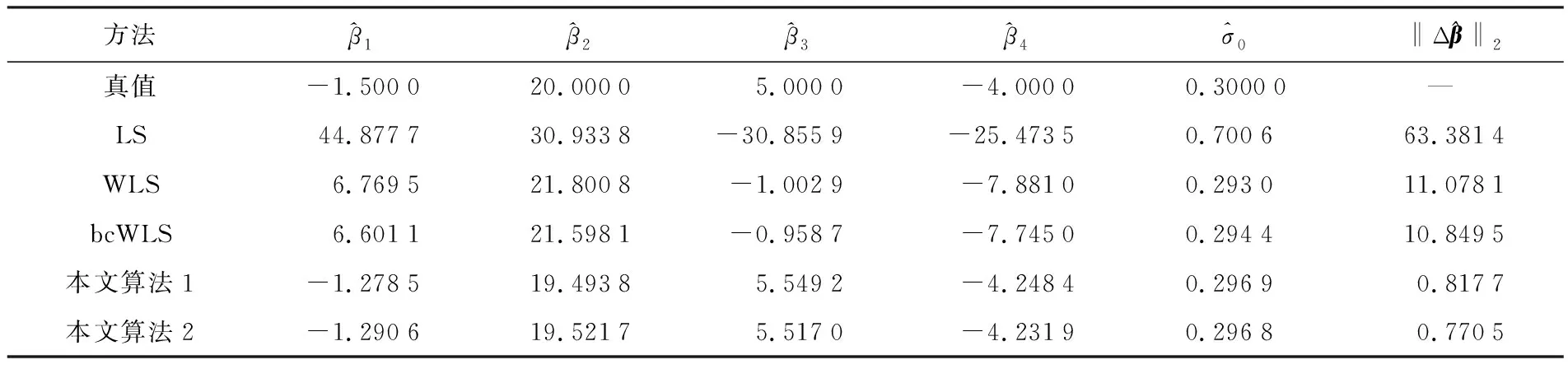
表5 参数估值、参数估值与真值之间的2范数和单位权中误差

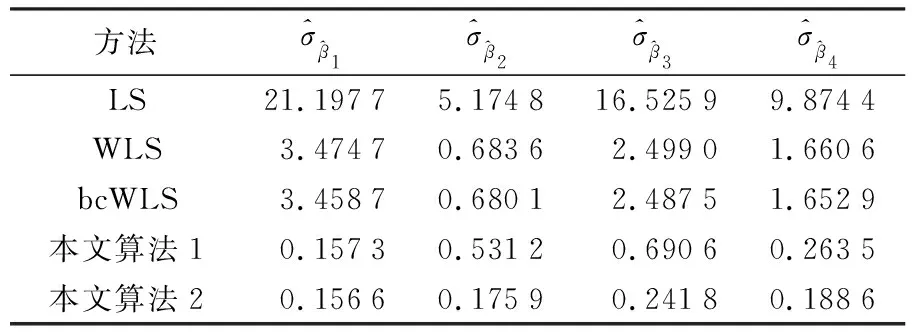
表6 参数估值的均方根误差

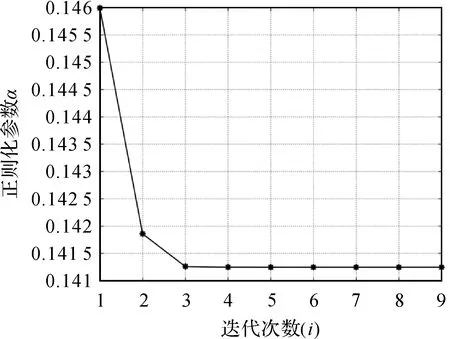
图6 正则化参数α随迭代次数的变化Fig.6 The regularization parameter with the number of iterations

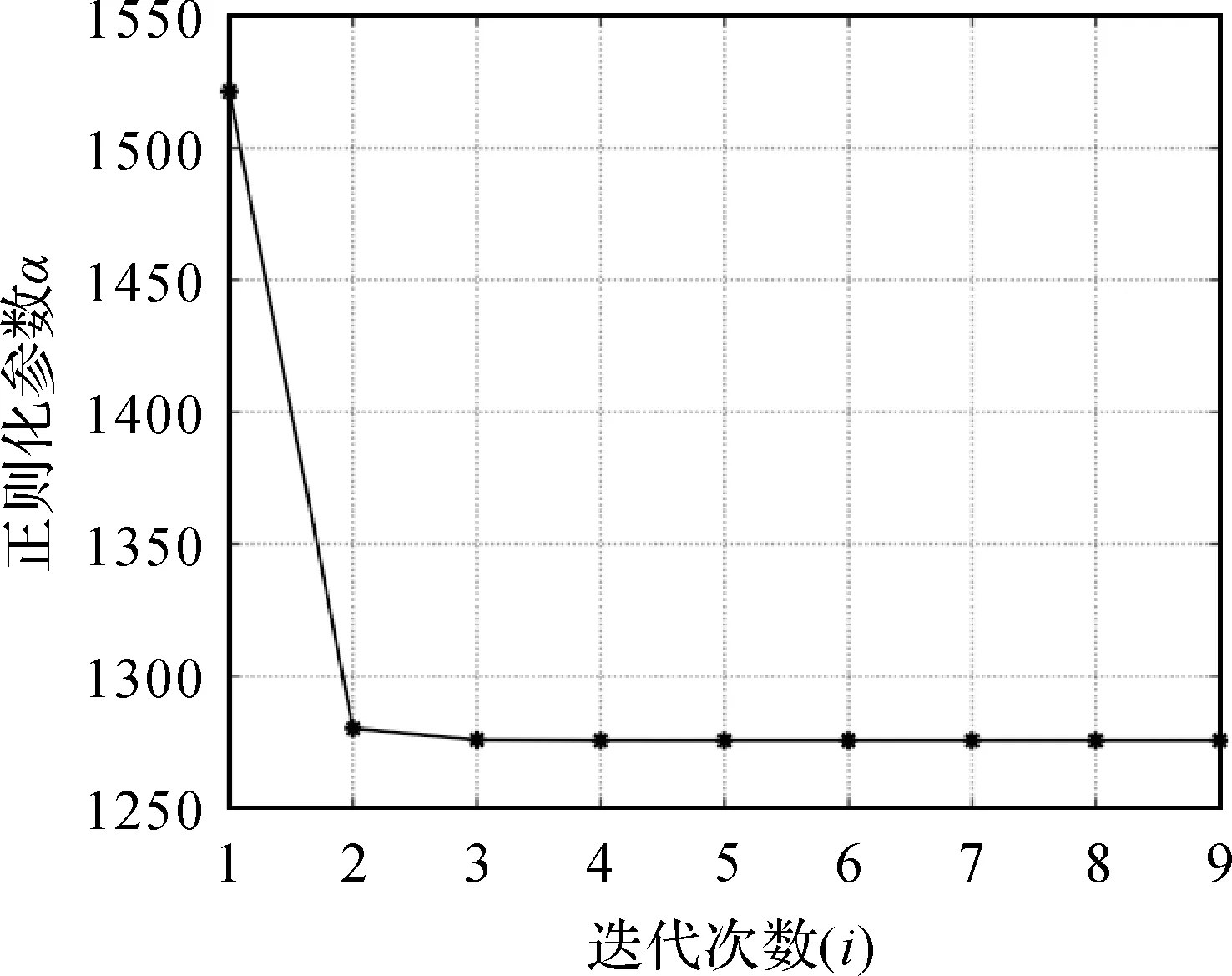
图7 法矩阵条件数随迭代次数的变化Fig.7 The condition number of the normal matrix with the number of iterations

由图4和图5可以发现，尽管本文模拟的DTM模型加入的乘性误差标准差仅为0.1，但对高程产生了较大的影响，此时法矩阵的条件数为5.190 5×104，严重病态。因此，针对病态乘性误差模型数据处理理论需要进行更深入的研究。

由表5可得，由于未考虑模型的病态性，文献[7]中的方法求得的参数估值严重偏离真值，而本文算法求得的结果更接近真值，参数估值的2范数分别为0.817 7和0.770 5，比bcWLS方法小了10.031 8和10.079 0，进一步说明本文算法对于降低病态性有一定的效果。其中，本文算法2考虑到非线性迭代的过程对参数估值的影响，求得的2范数最小，这与算例1得到的结果一致。由表5中的单位权中误差可知，LS方法求得的单位权中误差0.700 6，结果严重偏离真值；WLS方法和bcWLS方法由于考虑了观测值的权，求得的单位权中误差比LS方法更接近真值，为0.293 0和0.294 4；本文算法考虑了病态性对单位权中误差的影响，求得的单位权中误差最接近真值。

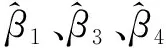
4.3 算例3

为进一步说明本文方法的可行性和适用性，算例3为一个病态数字高程模型真实数据算例。数字高程模型是一种承载地面高程信息的空间数据模型，是DTM模型的一个分支，本文主要利用SRTM(shuttle radar topography mission)提供的免费DEM数据集，通过在网站http:∥srtm.csi.cgiar.org/srtmdata/下载了2304个点的三维坐标数据来说明本文算法在实际应用中的优势。SRTM数据是由航天飞机雷达测量生成的LiDAR影像数据[37]，且LiDAR数据的噪声已被证明具有乘性噪声性质[38]，因此本文含有6个未知参数的数字高程DEM乘性误差模型如下

H(xi,yi)=F(xi,yi)⊙(1+εm)

(37)

式中，(xi,yi)表示地面点经纬度坐标；H(xi,yi)表示该点对应的高程，单位为米；εm表示乘性误差向量。

F(xi,yi)的具体形式如下[7]

(38)

由于SRTM数据均是在等精度测量中获取，因此在定权时假设未知的单位权中误差和乘性误差相等，即乘性误差的权阵为单位阵。本文获取的受乘性误差干扰的数字高程模型如图8所示，分别使用表1中的5种方案计算，WLS方法和bcWLS方法由于受病态性的影响，系数矩阵奇异，参数估值不收敛；LS方法、本文算法1和2方法拟合的数字高程模型如图9、图10和图11所示。将3种收敛方案计算的参数估值和单位权中误差估值列于表7，参数估值的均方根误差列于表8。

表7 参数估值和单位权中误差

表8 参数估值的均方根误差

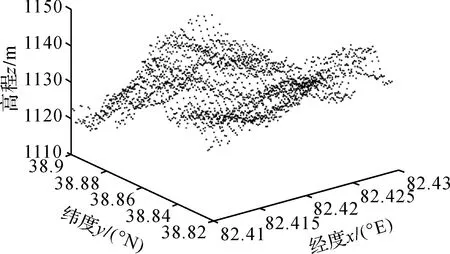
图8 受乘性误差干扰的数字高程模型Fig.8 Digital elevation model disturbed by multiplicative error

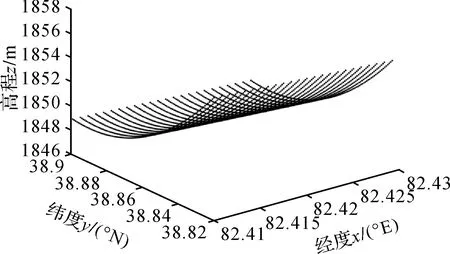
图9 LS方法求得的数字高程模型Fig.9 Digital elevation model obtained by the LS method

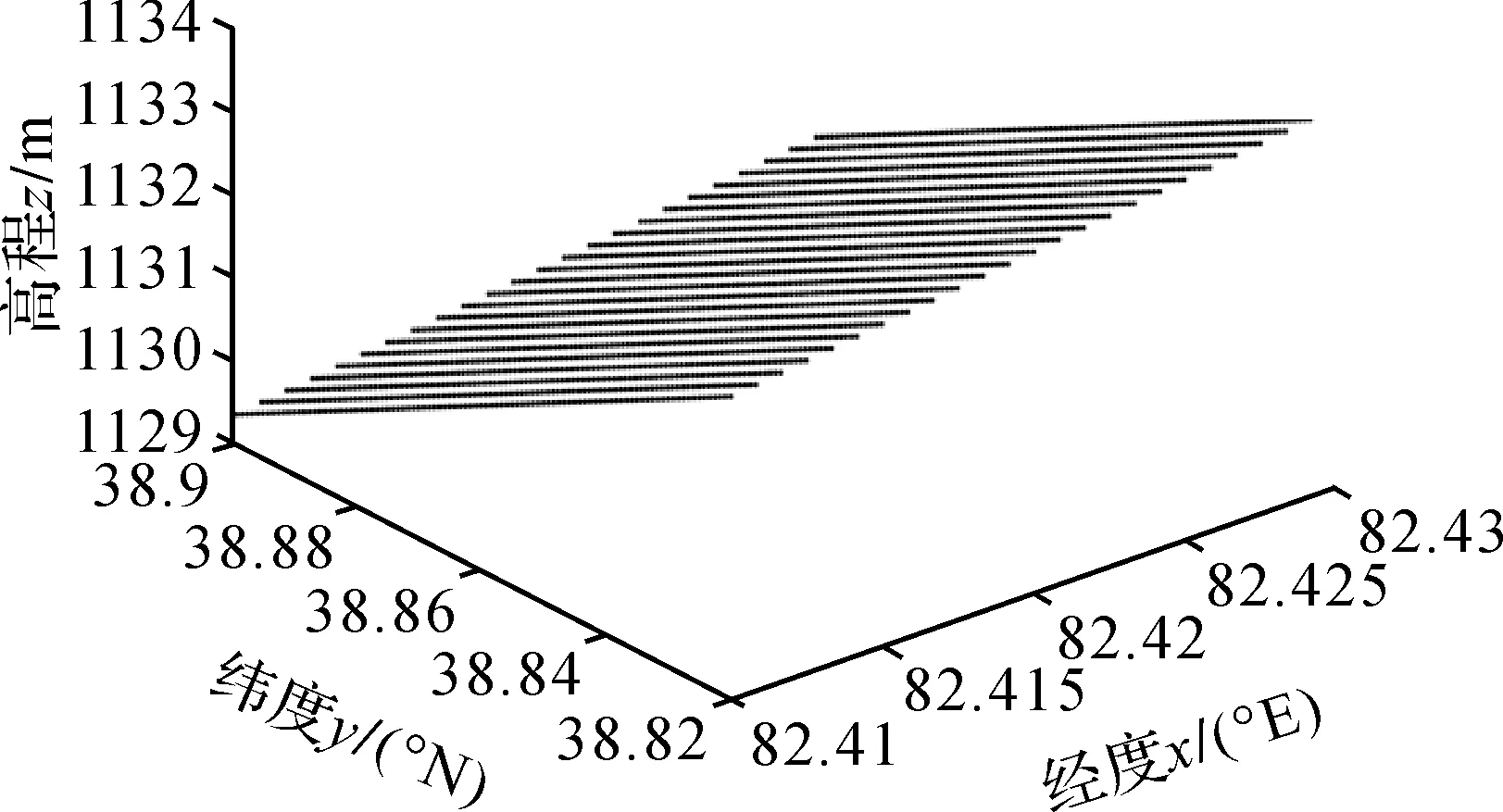
图10 RWLS方法求得的数字高程模型Fig.10 Digital elevation model obtained by the RWLS method

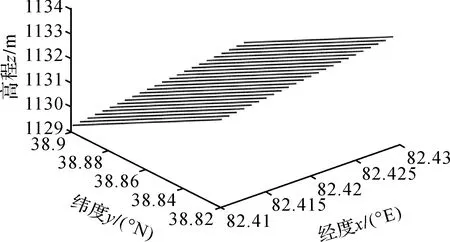
图11 SUTRWLS方法求得的数字高程模型Fig.11 Digital elevation model obtained by the SUTRWLS method

由图8和图9可以发现，LS方法求得拟合高程的结果严重偏离原始的数字高程模型，这是由于LS方法未考虑观测值的权且模型为病态性所导致的。本文算法考虑了病态性的影响，在处理实际数据时更具优势，从图10和图11来看，求得拟合高程的结果能够较好地拟合图8的高程。说明现有文献未考虑病态性的方法无法处理实际数据，因此顾及模型病态性带来的影响是十分必要的。

由表7可以看出，LS方法求得的参数估值和单位权中误差过大，不符合实际情况，进一步说明了LS方法无法处理实际数据，本文算法在处理实际数据的优势。由表8也可以看出，LS方法求得参数估值的根均方误差最大，本文算法远小于LS方法。其中，在本文算法中，由于算法2考虑了非线性迭代过程对参数估计带来的影响，使用SUT法求得的参数估值的均方根误差小于算法1，这也验证了本文算法的适用性和优势。对比算法1和算法2在参数估值上并没有很大差别，这可能是因为参数估值较小；而参数估值的均方根误差却差别很大，这是因为算法1根据误差传播定律求得的均方根误差只能反映参数估值的一阶精度信息，而算法2采用的SUT法为二阶精度评定方法，求得参数估值的精度信息为二阶精度。

5 结 论

为了完善乘性误差模型数据处理理论，本文在分析已有研究的基础上，将乘性误差模型扩展至病态乘性误差模型，推导了病态乘性误差模型参数估计的Tikhonov正则化迭代解公式。考虑到迭代过程中参数估值与观测值之间存在复杂的非线性关系，引入SUT法对病态乘性误差模型进行精度评定。最后，通过算例的验证与分析得到以下几点结论：

(1) 本文推导的病态乘性误差模型参数估计的Tikhonov正则化迭代解法可以得到比未考虑模型病态性的方法更准确的参数估值，且参数估值的精度更高。

(2) 通过将加权最小二乘正则化迭代过程表示成非线性函数，引入的SUT精度评定方法能够得到更为合理的精度信息。

(3) 本文提出的方法是基于函数f(·)为β的线性函数的情况下推导的，若将函数f(·)扩展至非线性函数，需要进一步研究。