从射影几何视角分析北京高考解析几何试题

2021-05-12北京市第五中学通州校区101101田朋朋

中学数学研究(广东) 2021年7期

北京市第五中学通州校区(101101) 田朋朋何伟

近年来,各地高考试题中以射影几何中极点极线、中心射影理论为背景的圆锥曲线题目层出不穷.本人在文[1]中分析了2019年北京高考数学文科解析几何试题命制的背景为射影几何中极点极线理论下的反演变换.本人在文[2]中借助射影几何中的极点极线、中心射影理论揭示了一类圆锥曲线中三直线斜率等差性质的本质,并推广出十个优美结论.分析试题背后的命题思路,有助于学生对试题结果进行猜想和假设,从而更好的书写过程和运算结果.同样对于教师,如果了解试题命制背后的思维逻辑,可以通过对高考试题进行横向、纵向研究,命制与高考相似的变式训练,对学生进行有针对性的思维训练,提高学生的逻辑思维能力.

1 射影几何相关理论

1.1 点列交比

若A,B,C,D四点共线, 则这四点A,B,C,D的交比(AB,CD) 定义为四条有向线段的比: (AB,CD) =若(AB,CD) =-1,则称点C,D调和分割点A,B,或称点A,B与点C,D调和共轭,A,B,C,D为调和点列.如图1.

特别地有: (1)最左(右)侧点到同侧三点的线段成调和关系:

(2)一线段被它的中点和这直线上的无穷远点调和分割.

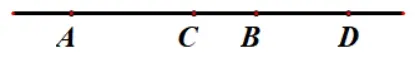
图1

图2

1.2 线束交比

若a,b,c,d是共点的四条直线, 则(ab,cd) =叫做a,b,c,d的交比.若四直线a,b,c,d满足(ab,cd)=-1,则称a,b,c,d调和共轭.如图2.

特别地有: (1)如果任意一条直线s截a,b,c,d四条直线于点A,B,C,D,则有(ab,cd)=(AB,CD).

(2) 若公共点记为P, 习惯上将(ab,cd) 记为P(AB,CD).

(3)若共点四直线a,b,c,d的斜率分别为k1,k2,k3,k4,则(ab,cd)=

(4)交比经中心射影后不变.

1.3 极点极线理论

如图3, 给定二次曲线C, 如果两点P,Q(P,Q不在曲线C上) 的连线与二次曲线交于两点M1,M2, 且(M1M2,PQ) =-1, 则称P,Q关于二次曲线C调和共轭,或称点Q与点P关于二次曲线C互为共轭点.

不在二次曲线上的一个定点关于一条二次曲线调和共轭点的轨迹是一条直线.若定点P关于二次曲线的共轭点的轨迹是一条直线,这条直线叫做点P关于此二阶曲线的极线,P点叫做这条直线关于此二次曲线的极点.若点P在二次曲线上,则点P的极线即为二次曲线在P点处的切线.

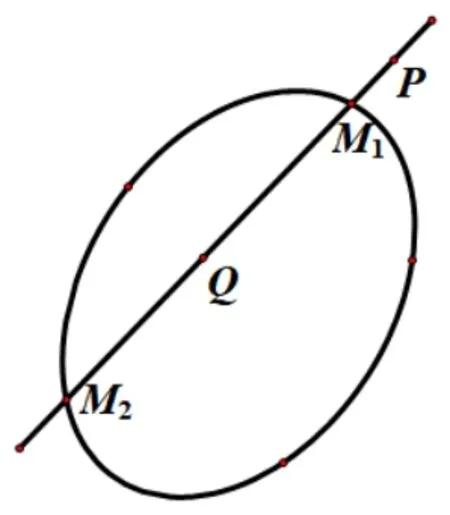
图3

图4

如图4,P为不在二次曲线上的点,过点P引两条割线依次交二次曲线于点E,F,G,H, 连接EH,FG交于点N,连接EG,FH交于点M,则MN为点P对应的极线.特别地,若P是二次曲线上的点,则过点P的切线即为极线.同理直线PN为点M对应的极线,直线PM为点N对应的极线.

在《高等几何》[3]中, 点P(x0,y0) 关于二次曲线C:Ax2+Bxy+Cy2+Dx+Ey+F=0 的极线方程为

即(2Ax0+By0+D)x+(Bx0+2Cy0+E)y+Dx0+Ey0+2F=0.特别地有:

(3)对于抛物线y2=2px,与点P(x0,y0)对应的极线方程为y0y=p(x0+x);

(4)圆锥曲线的焦点与准线是一对特殊的极点与极线.

限于文章篇幅,上述1.1 中的(1)和(2);1.2 中的(3)和(4);1.3 中的(1-4)在此不做证明,证明过程请参见文[4].

2 命题背景分析

试题1(2020年高考北京卷第20 题) 已知椭圆过点A(-2,-1),且a=2b,

(1)求椭圆C的方程;

(2)过点B(-4,0)的直线l交椭圆C于点M,N, 直线MN,MA分别交直线x=-4 于点P,Q,求的值.

分析如图5, 因为椭圆方程为= 1, 所以a2= 8, 点B(-4,0) 的极线为x==-2, 可知定点A(-2,-1) 在点B(-4,0) 的极线x=-2 上, 设极线x=-2 与线段MN交于点D,由极点极线的定义可知A(BD,MN) =-1,又因为交比在中心射影下不变,所以有A(BD,MN) =A(BB∞,PQ) =-1(B∞为点B的无穷远点).即线段PQ被点B和点B的无穷远点调和分割,所以点B为线段PQ的中点,因此

图5

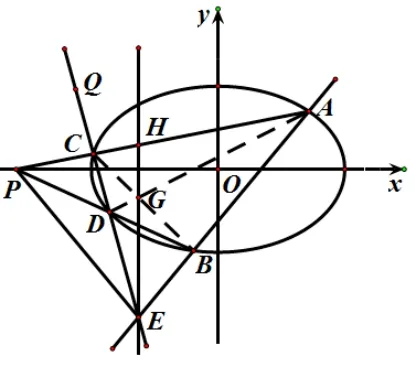
图6

试题2(2018年北京卷文科第20 题) 已知椭圆M:= 1(a ＞b ＞0) 的离心率为焦距为斜率为k的直线l与椭圆M有两个不同的交点A,B,

(1)求椭圆M的方程;

(2)若k=1,求|AB|的最大值;

(3) 设P(-2,0), 直线PA与椭圆M的另一个交点为C, 直线PB与椭圆M的另一个交点为D, 若C,D和点共线,求k.

分析本题与试题1 有着相同的几何背景,都是以椭圆为基础的中心射影结构.如图5,将本试题中椭圆上的四个点A,B,C,D退化为三个点(点B,D,E重合)后,就是图5 的几何结构.只不过试题2 是在解决以点E为中心射影的四条直线斜率关系问题,试题1 是在解决同一中心射影下交比不变的问题.

又因为直线EH垂直于x轴, 所以可认为kEH=∞, 则有= 1, 即kEP - kEC=kEB - kEP, 即2yE -4(yE -=k-2yE,解得k=1.

试题3(2018年高考北京卷理科第19 题)已知抛物线C:y2= 2px经过点P(1,2),过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于点M,直线PB交y轴于点N.

(1)求直线l的斜率的取值范围;

(2)设O为原点,为定值.

分析从射影几何的眼光下看,椭圆、双曲线、抛物线可看作圆在某一平面上的投影,三种曲线的各自定义、统一定义及其几何性质有着密切的联系.本试题与试题1 有着相同的几何背景,只不过将试题1 中的椭圆换成抛物线、x轴上的定点B(-4,0)换成y轴上的定点Q(0,1).

图7

具体分析过程如下: 如图7,连接OP交AB于点C,则直线OP方程为y= 2x.因为抛物线的方程为y2= 4x,所以点Q(0,1) 的极线为y= 2x, 即为直线OP.所以有P(AB,CQ) =-1,又因为交比在中心射影下不变,所以有P(MN,OQ) =P(AB,CD) =-1,即点M,N调和分割点Q,O.因此有

试题4(2017年高考北京卷理科第18 题)已知抛物线C:y2=2px过点P(1,1).过点作直线l与抛物线C交于不同的两点M,N, 过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点.

(1)求抛物线C的方程,并求其焦点坐标和准线方程;

(2)求证:A为线段BM的中点.

分析本题与试题3 的几何背景完全一致, 只不过本题中第二条截线为过点M且垂直于x轴的垂线; 试题3 中第二条截线为y轴.根据交比在中心射影下的不变性,本题第(2)问的结论又与试题1 完全一致.

图8

具体分析如下: 如图8, 连接OP交MN于点C, 则直线OP方程为y=x.因为抛物线的方程为y2=x,所以点的极线为y=x, 即为直线OP.所以有P(DC,MN) =-1.并且当点D,C,M,N为一组调和点列时, 以点P为中心的线束中直线的交比等于以点O为中心的线束之中直线的交比, 即P(DC,MN) =O(DC,MN) =-1.又因为交比在中心射影下不变,所以有O(DC,MN) =O(A∞A,MB) =-1(A∞为点A的无穷远点),即线段MB被点A和点A的无穷远点调和分割,所以点A为线段BM的中点.