浙江省宁波效实中学(315012) 鲁 勤 童益民

三面角模型是立体几何中的一个重要模型,三面角模型中蕴含了面角(线线角)、线面角与二面角,如何求这些角的大小以及它们之间的大小关系,成为高考的常规题型.通过对三面角模型的研究,可以得到一些定理,通过这些定理的灵活运用,可以较快的解决问题.同时对三面角模型的研究,可以提高学生对各类角的整体认识,提高他们的综合解题能力,培养数学建模的意识,发展数学核心素养.

一、几个定理的呈现

1.1 三面角余弦定理如图1, 由射线PA,PB,PC构成的三面角P - ABC中, ∠APC=α,∠BPC=β,∠APB=γ, 二面角A-PC -B的大小为θ, 则cosγ=cosαcosβ+sinαsinβcosθ.

图1

图2

图3

证明(1)当时,如图2,过射线PC上一点H作HM⊥PC交PA于M点,作HN⊥PC交PB于N点.在ΔMNP和ΔMNH中分别用余弦定理,得

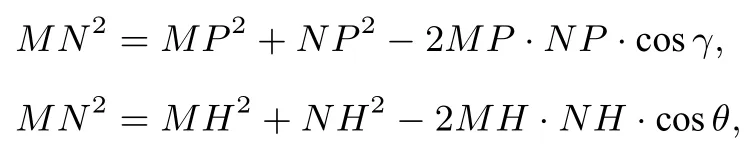
两式相减得MP2-MH2+NP2-NH2-2MP ·NP ·cosγ+2MH ·NH ·cosθ= 0, 所以2MP ·NP ·cosγ=2PH2+ 2MH · NH ·cosθ, 两 边 同 除 以MP · NP, 得cosγ=cosαcosβ+sinαsinβcosθ.

两式相减得MN2- M1N2=MP2- M1H2+NP2-NH2-2MP · NP ·cosγ+ 2M1H · NH ·cosθ, 所 以MM12=PH2-2MP ·NP ·cosγ+2M1H ·NH ·cosθ,所以NP ·cosγ=NH ·cosθ,两边同除以NP,得cosγ=sinβcosθ,符合cosγ=cosαcosβ+sinαsinβcosθ.

(3) 当α=时, cosγ= cosαcosβ+sinαsinβcosθ显然成立;

(4)当α ∈时, 可反向延长, 根据(1)(2)可证,略.

由(1)(2)(3)(4)可得,三面角余弦定理即证.三面角余弦定理中取二面角A-PC -B的大小θ=可得三余弦定理.

1.2 三余弦定理如图4, 已知平面α与斜线PA,AO⊥α,PB ⊂α,可得cos ∠APB=cos ∠APO·cos ∠BPO.

证明作OE⊥PB于E点, 连接AE, cos ∠APB=,cos ∠APO=所以cos ∠APB=cos ∠APO·cos ∠BPO.

推论1 最小角定理直线与平面所成角是直线与平面内所有直线所成角中最小的角.

证明如图4, 根据三余弦定理可得cos ∠APB≤cos ∠APO,所以∠APB≥∠APO,即证.

图4

图5

2.1 三面角正弦定理如图1, 由射线PA,PB,PC构成的三面角P - ABC中, ∠APC=α, ∠BPC=β,∠APB=γ, 二面角A - PC - B的大小为θ1, 二面角A-PB-C的大小为θ2,二面角B-PA-C的大小为θ3,则

证明在射线PA上取点D,作DO⊥平面PBC.

(1) 点O不在射线PB与PC上时, 如图5, 作OE⊥PB,OF⊥PC,连接DE,DF,

(2)点O与点P重合,显然成立.

(3)点O在射线PB或PC上时,如图6,作OE⊥PB,连接DE,

由(1)(2)(3)可得,三面角正弦定理即证.三面角正弦定理中取二面角A-PC -B的大小θ1=可得三正弦定理.

2.2 三正弦定理如图6,已知二面角A - PB - C中,D是PA上的点,DO⊥平面PBC,OE⊥PB,可得sin ∠DPO=sin ∠DPE·sin ∠DEO.

图6

证 明因为 sin ∠DPO=sin ∠DPE=所 以sin ∠DPO= sin ∠DPE ·sin ∠DEO.

推论2 最大角定理二面角是所有线面角中的最大角.

证明当二面角大于或等于时, 显然成立; 当二面角小于时, 如图6, 根据三正弦定理可得sin ∠DPO≤sin ∠DEO,所以∠DPO≤∠DEO,即证.

二、几个定理的应用

题1(2018年高考浙江卷第8 题) 已知四棱锥S -ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成角为θ1,SE与平面ABCD所成角为θ2,二面角S-AB-C的平面角为θ3,则

A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1

C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1

解析根据最小角定理可得θ2≤θ1,排除选项A 与C,根据最大角定理可得θ3≥θ2,排除选项B,可得答案D,当然通过作图计算,也可得θ3≤θ1.

题2(2019年高考浙江卷第8 题)设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱V A上的点(不含端点).记直线PB与直线AC所成的角为α,直线PB与平面ABC所成的角为β,二面角P -AC-B的平面角为γ,则

A.β ＜γ,α ＜γB.β ＜α,β ＜γ

C.β ＜α,γ ＜αD.α ＜β,γ ＜β

解析根据最小值定理可得β ＜α; 根据最大角定理得到β小于二面角P - AB - C的大小, 因为二面角P-AC-B与二面角P-AB-C的大小一样,所以β ＜γ,可得答案为B.

题3(2009年高考浙江卷理科第17 题) 如图7, 在长方形ABCD中,AB= 2,BC= 1,E为DC中点,F为线段EC(端点除外) 上一动点.现将ΔAFD沿AF折起, 使平面ABD与平面ABC垂直.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是_____.

图7

解析因为平面ABD⊥平面ABC,DK⊥AB, 所以DK⊥平面ABC, 在三面角A - DBF中, 根据三余弦定理, 可得cos ∠DAF= cos ∠DAB ·cos ∠BAF, 所以所以AK=

题4(2020年高考浙江卷第19 题) 如图8, 三棱台ABC - DEF中, 平面ACFD⊥平面ABC, ∠ACB=∠ACD=45°,DC=2BC.

(1)证明:EF⊥DB;

(2) 求直线DF与平面DBC所成角的正弦值.

解析本题直观上是一个棱台中的角度问题,但本质上是一个三面角C-ABD的角度问题.

图8

(1) 作DG⊥AC于G点, 连接BG, 如图8.因为平面ACFD⊥平面ABC, 所以DG⊥平面ABC, 根据三余弦定理, 得cos ∠DCB= cos ∠DCG ·cos ∠BCG, 所以cos ∠DCB=即∠DCB= 60°,因为DC= 2BC,可得BC⊥DB,因为EF//BC,所以EF⊥DB.

(2) 因为DF//AC, 所以直线DF与平面DBC所成角就是直线AC与平面DBC所成角, 因为∠ACB=∠ACD= 45°,所以AC在平面DBC上的射影为∠BCD的角平分线, 设AC与平面DBC所成角为φ, 根据三余弦定理得cos 45°= cosφ·cos 30°, 所以cosφ=所以即直线DF与平面DBC所成角的正弦值为

三、探究与拓展

探究1根据三面角余弦定理,已知三个面角可以求出二面角,根据三面角正弦定理,已知两个面角和一个相对二面角,可以求出另一个相对二面角,那么已知三个面角是否可以求出线面角呢?

结论1在三面角P -ABC中,∠APB=α,∠APC=β,∠BPC=γ,直线PA与平面PBC的所成角的大小为φ,则cosφ=

证明如图9,在射线PA上取点D,作DO⊥平面PBC,OE⊥PB,OF⊥PC,连接DE,DF.

因为P,E,O,F四点共圆,则

图9

图10

探究2在三面角的三条射线上取三个点,得到一个三棱锥,能否得出三棱锥的体积公式?

结论2在三棱锥P -ABC中,∠APB=α,∠APC=β, ∠BPC=γ, 则VP-ABC=PA · PB · PC ·

证明如图10,设直线PA与平面PBC的所成角的大小为φ,根据结论1,

所以

所以

题5(2016年高考浙江卷理科第14 题)如图11,在ΔABC中,AB=BC= 2,∠ABC= 120°.若平面ABC外的点P和线段AC上的点D, 满足PD=DA,PB=BA, 则四面体PBCD的体积的最大值是_____.

图11

解析设∠PBD= ∠ABD=α, ∠PBC=β,∠CBD= 120° - α=γ.在ΔABD中, 根据正弦定理,可得所以BD=根据结论2,可得

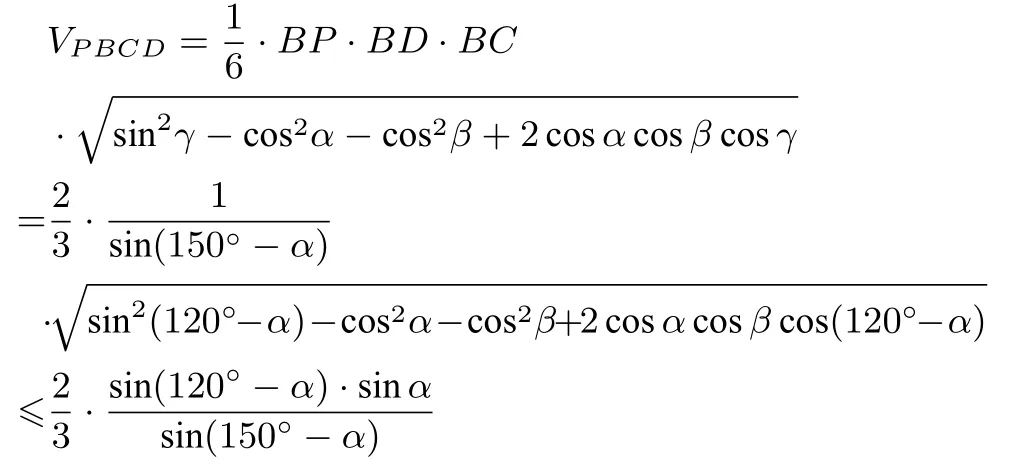
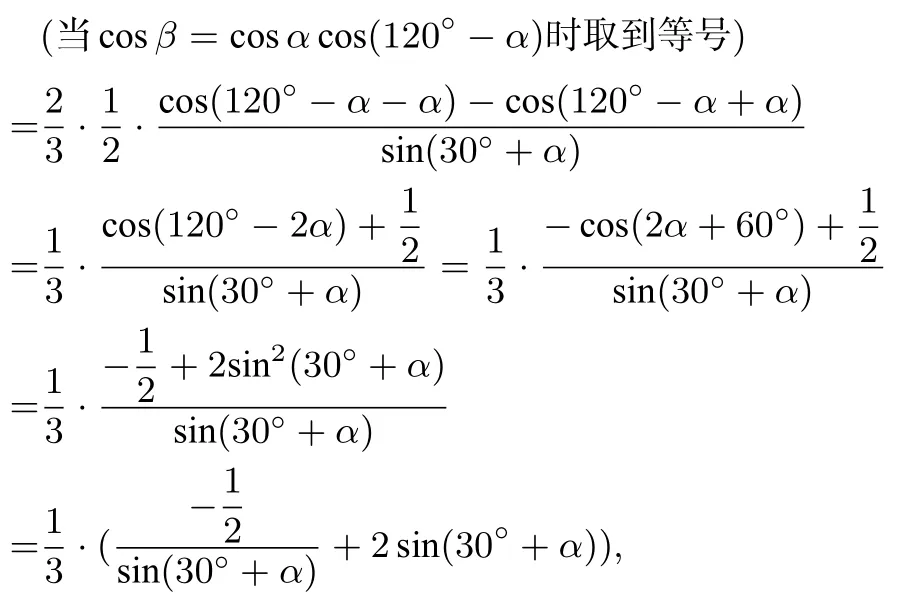
所以当α=60°时,VP BCD取到最大值为

四、总结

以上是基于三面角模型中角度问题的研究,从三面角余弦定理到三余弦定理,再到最小角定理,同样从三面角正弦定理到三正弦定理,再到最大角定理,系统的了解了其中所涉及的一系列定理,最后从探究与拓展的角度给出关于线面角和体积的两个结论,整体上去把握三面角模型中所涉及的问题.文中给出的几个例题,从解法上来说不是最常规的解法,但从三面角模型的角度问题能较快的得到答案,也是值得研究的地方.