文|鄢晓钦

解题能力是学生学业水平的一个重要体现，在解题的过程中可以检测到学生对数学基础知识、基本技能、基本思想、基本活动经验的掌握程度；同时检验教学是否充分落实了“四基”的培养。学生面对数学问题，运用数学知识，通过观察、分析、对比、推理、计算等方法能否顺利解决问题，其中体现出的就是学生的数学解题能力。因学生个体学业水平不同导致解题能力各异，于是，如何提高学生的解题能力，成为一个长期研究的具有实际意义的课题。但纵观各级各类相关课题研究，发现一线教师把更多的视角放在了数学解题技巧和解题方法的训练上，这在一定程度上确实在短期提升了学生的解题能力；但从长远来看，并没有对学生的解题能力达到质的提升，究其原因何在？我带领我的数学团队从数学的本源进行研究。数学是什么？数学是研究数量关系和空间形式的科学，而数学思想是数量关系和空间形式反映到人的意识再经过思考后的产物，它是对数学的本质认识。因此数学思想是数学的精髓，应用在解题中能准确把握到解题的关键点，是从知识到能力的转化器，它会在关键处启迪学生的思路，让学生的解题走向直观化、简约化、系统化，从根源上提升了学生解决数学问题的能力。本文将结合实例来阐述如上观点。

一、数形结合——让解题走向直观化

解题的直观化指的是能将抽象的数学问题进行直观地呈现，抽象是数学的本质，但学生的年龄特点决定了他们是以直观形象思维为主来思考问题的。当学生面对用枯燥文字和简单的数学符号呈现出的数学问题或用单一的图形表达复杂数学关系时，用形象思维去理解抽象的数学问题是解题的直接障碍。数形结合思想是将原本抽象、机械的数式与直观可感的图形进行有机融合，让学生经历从图到数，再从数到图的转化过程，提炼出核心的数量关系，帮助学生深入理解算理。它的本质是用数的规范和精确阐明形的属性，用形的直观和生动来表达数的关系，将抽象的数学表达与直观的图形结合起来。在解题时能根据需求渗透数形结合数学思想，让抽象的数与形进行互换，形象思维与抽象思维进行融合，能化抽象为具体，让解题走向直观化，降低思维的难度，顺利解题。而且数形结合的直观想象，也是数学十大核心素养中重要的数学素养，在解题的过程中能得到很好地培养，并借此进一步提升了学生的解题能力。

对本题做了一个前测，40位学生参加，正确率为42.5%，在访谈中让学生回顾解题思路，学生的反馈是题目太难，无从思考，凭感觉和猜测完成的。本题表述精简、数据单一，难在哪里呢？难在解答时需要学生有很强的空间想象能力和抽象思维能力，要能从精简的表述中提炼出关键的数量关系进行分析进而解决。数形结合数学思想的渗透，突破了解题的难点，将抽象的数学问题用形象的图形呈现，在直观的观察中，把握住了解决问题的本质。

二、代换——让解题走向简约化

解题简约化指的是将复杂的解题方法用简约的方式替代，以求达到高效的解题效果。“代换”作为一种数学思想，在小学更多的意为“等量代换”，指的是用一个量取代与之相等的量。因为当两种事物的量刚好在某方面平衡时，可以互相替代，替代的目的是为了将求解对象化为统一，将两个未知量统一为一个未知量求值，然后间接求出另一个未知量。代换是代数思想的基础，在运用中提取出代换的两个要素：代换对象和被代换对象，它们代换之后，能直观地看出数学问题中量与量之间的关系，让繁杂的思路简约化、让抽象的问题具体化，让复杂的计算简单化，帮助学生分析问题，理清解题思路。

如：请计算出下图阴影部分的面积。（单位：厘米）

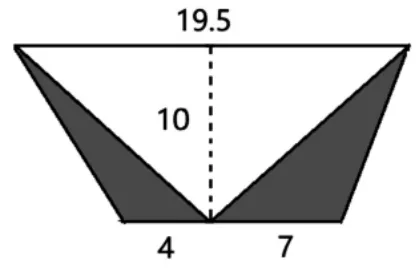
学生按照常态的解题思路是：阴影部分的面积等于梯形的面积减去里面空白部分三角形的面积：

S梯形=（a+b）h÷2 =（4+7+19.5）×10÷2=152.5（平方厘米）

S三角形=ah÷2 =19.5×10÷2=97.5（平方厘米）

S阴影部分=152.5-97.5=55（平方厘米）

在解决问题的过程中，运用了求两个平面图形面积的计算公式，相应就有了大量的数据计算，知识点与数据的增加加大了解题的难度。而且常态的解题方法体现了学生浅层次的数学思维和思考问题的能力，不利于培养和提高学生的解题能力。因此，可以引导学生换一个角度，运用等量代换的数学思想，感受解题的简约化。

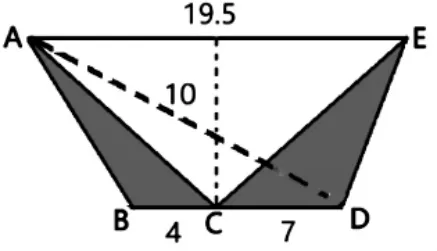
如图，在原题图形中添加了一条辅助线AD，通过观察，发现△CDE 与△ACD 是同底等高的两个三角形，它们的面积相等，可以进行代换。因此，要求阴影部分的面积，就可以直接求△ABD 的面积：S=ah÷2=（4+7）×10÷2=55（平方厘米）。

等量代换数学思想的渗透运用，让学生感受到代换思想的意义，体会便捷解题的同时，形成代换的解题意识，形成代换的解题思路和敏锐的策略意识，简约解题，提升数学的思考能力，从本质上提升解决数学问题的能力。

三、建模——让解题走向系统化

系统化解题指的是将同一种类型的数学问题进行归类建模，然后用相应的方法解决此类问题，达到解决一个问题走向解决一类问题的效果。建模即建立模型，为了更深刻地认识理解某一事物，对事物作出抽象和表述的过程。数学上的建模是建立数学模型，运用抽象和简化的数学方法除去实际问题的非本质属性，保留其重要元素和本质属性，形成一种数学结构。因此，数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养。数学建模是数学学科重要的核心素养，培养学生数学建模的能力，将建模的数学思想渗透到解决数学问题中，会让同一类型的问题找到其相同的特征，运用模型的公式、方法分析其中的数量关系，让复杂的问题模型化，提升学生解决问题的能力。

如行程问题中常有几种类型：

1.相向也相遇的情况。

甲乙两人同时驾车分别从AB 两地相对开出，甲车每小时行驶50 千米，乙车每小时行驶60 千米，5 小时后两车相遇，AB两地相距多少千米？

2.相向未相遇的情况。

AB 两地相距550 千米，甲乙两人同时驾车分别从AB 两地相对开出，甲车每小时行50千米，乙车每小时行驶60 千米，4 小时后两车相距多少千米？

3.相向相遇又相距的情况。

AB 两地相距550 千米，甲乙两人同时驾车分别从AB 两地相对开出，甲车每小时行50 千米，乙车每小时行驶60 千米，6小时后两车相距多少千米？

这三道不同类型的现实问题，通过数学建模的方式，可以归纳为同一类型的数学问题，即行程问题。第1 题是数学中行程基础的相遇问题，首先通过数学抽象，提炼出数学的信息和问题，知道甲乙两车的速度和两车的相遇时间，求AB 两地相距的路程，也就是两车已经行驶的路程。其次，通过画图、分析解决了数学问题，方法一：50×5+60×5=550（千米）；方法二：（50+60）×5=550（千米），优化推出第二种方法。最后在解决问题的过程中帮助学生建立起行程中相遇问题的数学模型：速度和×相遇时间=路程。

第2 题是两车相向行驶但未相遇的情况，学生明确用总路程-已经行驶的路程=未行驶的路程=两车相距的路程。但总路程如何求出？运用第1 题建立的数学模型，求路程用公式：速度和×相遇时间=路程，求出两车共同行驶的路程，然后列式 计 算：550-（50+60）×4=110（千米）。在这个过程中，数学模型的运用，成功地将数学问题纳入对应的模型问题，难点就得以突破。

第3 题是相向相遇又相距的情况，运用“速度和×相遇时间=路程”这个数学模型公式，首先求出了两车一共行驶的路程，然后用路程-路的总长度=两车相距的路程，（50+60）×6-550=110（千米）。

三道看似不同类型的数学问题，通过分析，在解答中找到了它们的共性，并将它们构建成一种模型的数学问题，它们是行程问题中的不同形式，只是将数学信息和问题进行不断地变化，变化中抓住解题的本质，都是行程问题，都要求出两车已经行驶的路程，运用重要的模型公式：速度和×相遇时间=路程，让问题迎刃而解。数学模型的成功建构，会让学生今后面对同类问题时，能自觉地将问题纳入已有的模型问题中，运用模型问题相对应的方法来解决数学问题，将具体问题转化为数学模型进行数据量化，完成对问题的解答。在这样解决问题的过程中，学生通过一道题，运用迁移的方法，解决一种类型的问题，让问题归类形成系统性，进一步提高了解决问题的能力。

综上所述，依托相应的数学思想，准确理解题意、把握问题的本质、提取数量关系、分析解答数学问题，从中锻炼了学生的数学思考和解决问题策略的运用，让解题的走向直观化、简约化、系统化。直观化降低了解题的难度；简约化感受了解题的便捷并提升了解题的数学思维；系统化构建了数学问题模型。三种解题能力的形成，真正促使学生从浅层面解决数学问题到灵活、深层次解决问题，本质上提升了解决问题的能力，这也是数学育人的真正追求。