文|方 芳

【教学内容】

苏教版五年级下册第96、97 页。

【教学过程】

一、确定圆面积的范围，初步感知极限思想

师：今天我们一起来研究“圆的面积”，先来完成一份《学习单》，通过数和算，你能发现圆的面积与它的半径有什么关系吗？

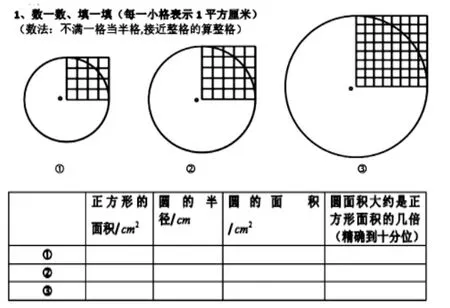
生：圆的面积大约是正方形面积的3 倍多。

生：圆的面积大约是r2的3倍多一些。

师：那如果半径是20 呢？如果这个圆再大呢？如果这个圆无限大呢？

生：圆的面积大约在r2的3倍与4 倍之间。

小结：看来这种方法并不能准确得到圆的面积，只能得到圆面积的范围。

【设计意图：在探究圆面积的过程中，首先引领学生感受圆面积的大小范围，巧妙地将“圆的面积大约是它半径平方的几倍”转化成“圆的面积大约是正方形面积的几倍”，让探究更具有可操作性和可视性。借助半径为4、5、8的三个圆以及继续想象半径为20 的圆，通过数方格的方法，初步感知圆的面积和r2之间是“3倍多一些”的关系，但这还不是很准确，因此教学中为了让学生更加清晰地感受到半径变大后圆的面积与r2的关系，随后提出猜想，如果这个圆无限大呢？学生经过思考后提出S=πr2的猜想。这样的教学过程能够让学生初步接触极限思想，感觉到无限大的圆就是一种极限情况，初步感知和体验极限思想的魅力。】

二、推导圆的面积公式，相机渗透极限思想

1.实践运用刘徽割圆术，探究圆与正多边形的关系。

师：同学们，今天的研究将围绕历史上三位著名的数学家展开。我们先来听第一则“刘徽与圆面积公式”的故事。公元263年，我国数学家刘徽在为《九章算术》作注时，称：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”你们听过吗？

操作一：正向操作，将正方形的纸剪成一个圆形。

师：你能将正方形的纸剪成一个最大的圆形吗？可以怎样剪？

师：有的同学是对折剪一个半圆，有的同学对折两次再剪，想一想，怎样剪才能让展开的图形更接近圆呢？

生：对折无数次。

师：的确，对折的次数越多，剪直线段，就越接近圆。如果能将纸片对折无数次，再用剪刀沿直线段剪开，就会得到一个近似的圆。

几何画板演示正多边形逼近圆的过程：

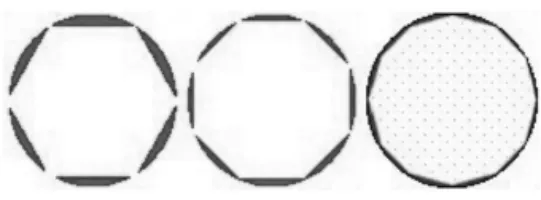
师：通过剪圆的过程我们感受到“方中有圆”，这对求圆的面积有启发吗？

生：可以把圆的面积看成一个正多边形的面积。

操作二：反向操作，将圆形的纸剪成正多边形。

师：现在反过来，你能把一张圆形纸片剪成正多边形吗？

（学生操作）

师：通过操作我们可以发现，圆对折的次数越多，正多边形和圆面积的差值越小，如果无限次对折，那么面积就相等了。

师：现在你们能再说说数学家刘徽所说的话是什么意思吗？

生：“割之弥细，所失弥少”就是随着圆内接正多边形的边数不断增加，正多边形的面积与圆的面积就越来越接近，当边数多到不能再加的时候，圆内接正多边形就与圆一样了。

【设计意图：学生经历两次操作，探究圆和正多边形的关系，利用正多边形来不断逼近圆的面积。两次操作从圆的外部和内部分别逼近圆，也涉及到阿基米德的“双侧逼近法”。通过几何画板的直观演示和对刘徽割圆术的进一步理解，让学生了解到数学家也是利用求圆内接正多边形的面积来求圆的面积，圆被分割得越细，正多边形的面积就越接近圆的面积，在极限状态下，正多边形的面积就等于圆的面积。正是有了两次实际操作的经历，学生对“割圆术”的理解不仅仅停留在字面意思，还能在亲身亲历中应用割圆术的原理，对极限思想的运用有更深的体会。】

2.经历开普勒分割变形法，转化图形推导面积公式。

师：刚才数学家刘徽的故事告诉我们求圆面积的过程是把圆转化成正多边形来研究的，那怎样计算圆的面积呢？我们来看第二个数学家的故事。17 世纪，德国著名天文学家、数学家开普勒在一次喝酒时发现酒桶各异，于是开始思考葡萄酒桶体积的算法，要解决这个问题，就要先求出圆的面积公式。经过思考，他想出了一种方法，叫做“分割变形法”，即把圆转化成已经熟悉的图形。你们想直接看他的方法还是自己先试一试？

（学生自主活动后汇报）

方法一：将圆转化成平行四边形。

生：我把圆平均分成8 份。

生：我平均分成了16 份。

生：我平均分成了32 份，更像长方形了。

师：当我们将圆平均分成8份，通过分割拼接可以得到这样的图形（图a），当圆被平均分成16 份时，我们可以将其转化成这样的图形（图b），当圆被平均分成32 份时，就转化成这样（图c）。仔细观察，你有什么发现？（转化后的图形越来越接近于长方形，转化前和转化后的图形的面积相等）

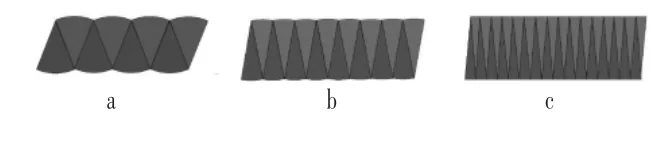
师：如果再继续分下去，转化后的图形会怎样变化？面积呢？

师：将这个圆平均分成无数份时，转化后的图形就成了（长方形）。此时转化前的图形和转化后的图形有什么联系？（面积不变）求圆的面积就转化成求这个长方形的面积。长方形的面积怎么算？

生：长方形的面积=长×宽，长=圆周长的一半，宽=圆的半径，所以长方形面积＝πr×r＝πr2。

师：刚才通过转化的方法将圆转化成与它等积的我们熟悉的长方形来研究，推导出了圆的面积的计算方法。还有不同方法吗？

方法二：将圆转化成三角形。

生：正多边形沿半径分割出来的图形可以看成一个一个等腰三角形，我们算出一个三角形的面积，再乘小三角形的个数。具体来说就是小等腰三角形的底＝圆的周长÷分成的份数n，它的高相当于圆的半径，所以S＝2πr÷n×r÷2×n＝πr×r＝πr2。

生：也可以转化成三角形或梯形，都需要想象分成无数份进行计算。

师：同学们特别厉害，自己想出了这么多转化计算的方法，现在我们来看看开普勒的方法。（出示图，图略）刚才这位同学的推导过程就有数学家开普勒的分割变形法的影子，很多同学都能想到极限的情况下可以把曲线看成直线，化曲为直，你们真了不起！

【设计意图：在学生推导圆面积的计算公式时，开普勒的分割变形法也已经悄然发生，学生在不知不觉中亲身经历了数学家的推导方法，体味到成功带来的喜悦，也更加真切感受到数学的极限思想。数学家的方法就是学生感受数学思想的一个有力支点，让学生借助数学家们的探究过程了解、体会数学中的极限思想和化曲为直的思想。】

3.材料阅读重温数学经典，了解阿基米德同心圆法。

师：最后一起来看第三位数学家阿基米德与圆面积公式的故事。公元前3 世纪，古希腊数学家阿基米德在《圆的度量》中说：圆面积等于“一条直角边长等于圆半径，另一条直角边长为圆周”的直角三角形面积。他是这样发现圆面积计算公式的，如下图，将圆从圆心开始直到边缘分成一些细窄的同心圆环，并逐一展开叠成一个直角三角形，将圆无限细分时，圆面积与直角三角形面积就近似相等。

师：看完阿基米德的方法，你有什么收获和感受？

生：我觉得不一定要拼成一个直角三角形，摆成等腰三角形也是一样的道理。

生：阿基米德也要把圆进行无限分割，找到一个极限状态。

生：数学家们很厉害，想出了很多不同推导圆面积计算公式的方法。

【设计意图：数学史中，不同的数学家不断创新，创造了很多方法探索圆面积的计算公式，在学生已经了解不同的圆面积公式推导方法的基础上，再次提出新的方法，让学生领悟数学家们的创新精神，学习数学家们对知识孜孜不倦追求的态度，同时也对圆面积计算公式的认识进行升华，进一步体会极限思想。】

三、回顾探究活动过程，深刻领悟极限思想

师：同学们今天研究得特别好，学习了这么多圆面积推导的方法，个个都是小数学家。那这么多的方法中你最喜欢哪种方法？为什么？在学习中感受到哪些数学学习的方法和思想？

生：我喜欢转化成长方形的方法，我觉得长方形的面积很好算，而且和圆的半径很好关联，计算方便，感受到了极限的思想方法。

生：我喜欢阿基米德的方法，很有创意，也要想象极限情况。

生：我觉得看成小三角形算再乘个数的方法简单，算其中一部分再算整体，算一个小三角形时也是按照极限情况算的。

师：的确，这几位数学家和同学们的方法都蕴含了一种重要的数学思想——极限思想。下面我们一起来看两个问题，看看你能不能解决。

问题1：已知一个圆的周长是31.4 米，求这个圆的面积。

问题2：将一个圆沿半径剪开，平均分成若干个完全相同的小扇形，割拼成近似的长方形，这个长方形和圆相比，说法正确的是：A.面积不变，周长增加；B.面积不变，周长减少；C.面积不变，周长不变。

师：课后，给你的爸爸妈妈介绍一下圆面积公式的推导过程，也去查一查还有哪些推导圆面积的方法，比如意大利数学家卡瓦列里的“棉线法”等等。

【设计意图：课堂小结和练习环节让学生回顾所有的推导过程，选出自己喜爱的方法，既是对计算方法的巩固，又是对数学思想方法的再感悟。练习中仍然选择经典的历史问题，学生翻译并解决，感受世界和中华古代文明的博大精深，同时注意把面积和周长联系在一起，让学生利用周长的一半×半径的方法解决。最后查阅其他方法的任务则是引导学生向数学家们学习，不要停下研究的脚步，延续学生对数学史的兴趣和热情，延续对数学极限思想的感悟。】