Jiangyuan Qu,Nana Qi,*,Kai Zhang,Lifeng Li,Pengcheng Wang

1 Beijing Key Laboratory of Emission Surveillance and Control for Thermal Power Generation,North China Electric Power University,Beijing 102206,China

2 Key Laboratory of Power Station Energy Transfer Conversion and System(North China Electric Power University),Ministry of Education,Beijing 102206,China

3 Shanxi Hepo Power Generation Company Limited,Yangquan 045011,China

Keywords:Wet flue gas desulfurization Gas–liquid flow Eulerian–Lagrangian model Flow pattern Transport processes Absorption

ABSTRACT Wet Flue Gas Desulfurization(WFGD)unit based upon spray scrubber has been widely employed to control SO2 emissions from flue gas in coal-fired power plant.To clarify the dependence of desulfurization performance on inter-phase transfer behaviors with non-ideal contacting patterns of flue gas and slurry droplets,three regions in spray scrubber are distinguished in terms of gas-slurry flow structures using CFD method in the Eulerian–Lagrangian framework.A comprehensive model is established by involving the transfer process between two phases and chemical reactions in aqueous phase,which is validated with the measured data from a WFGD scrubber of 330 MW coal-fired power unit.Numerical results show that the overall uniformity degree of flue gas in whole scrubber is largely determined by the force-balanced droplets in the middle part of scrubber,which is dominated by counter-current mode.Both momentum transfer behavior and SO2 chemical absorption process present the synchronicity with the evolution of gas-slurry flow pattern,whilst the heat transfer together with H2O evaporation has little effect on overall absorption process.Three regions are firstly defined as Gas Inlet Region(GIR),Dominant Absorption Region(DAR)and Slurry Dispersed Region(SDR)from the bottom to top of scrubber.SO2 is mainly scrubbed in DAR,which provides much more intensive interaction between two phases compared to GIR or SDR.A better understanding of the desulfurization process is obtained from the fundamental relationship between transport phenomena and chemical reactions based upon the complicated hydrodynamics of gas-slurry two-phase flow,which should be useful for designing and optimizing the scrubber in coal-fired power unit.

1.Introduction

Sulfur dioxide(SO2)is known to have detrimental impacts on air quality and human health,which causes a series of environmental pollutants such as acid rain and sulfate particulate matters[1,2].Wet Flue Gas Desulfurization(WFGD)technology has been widely employed to control SO2emissions from coal-fired power plants since the acidity of aqueous solution can be neutralized by alkaline absorbents,including Ca(OH)2[3],Mg(OH)2[4],CaCO3[5],seawater[6]and ammonia [7].As a result,various types of wet scrubbers,such as packed column[8],bubbling bed[9]and spray scrubber[10],have been developed to absorb SO2from the flue gas in coal-fired power units.Up to now,the spray scrubber using limestone as SO2absorbent is the most common WFGD technique due to low operational cost and high absorption efficiency[1,11,12].The significant advantage of spray scheme is to generate large interfacial area,which is beneficial to the wet scrubbing system for SO2dissociation[13–15].The desulfurization process taking place in the spray scrubber can be represented by the following overall reaction[12]:

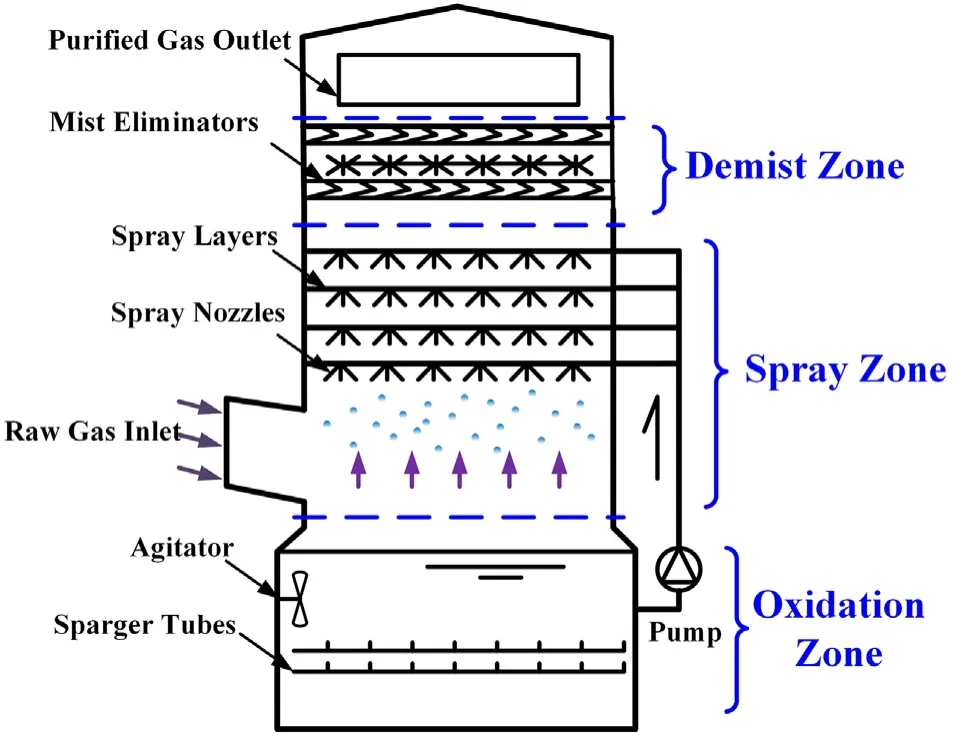
Fig.1.Schematic of WFGD spray scrubber.

As illustrated in Fig.1,a typical WFGD spray scrubber is comprised of spray zone,demist zone and oxidation zone.In the spray zone,the slurry droplets containing limestone are injected from the atomization nozzles positioned on spray layers,and the raw flue gas from the inlet of scrubber contacts with these falling droplets in an approximate counter-current mode.The SO2in flue gas is partially absorbed into the droplets,which associates with the complicated processes of gas-slurry heat transfer,H2O evaporation and acid–base reactions [16].Then these droplets entrained by flue gas are captured in the demist zone,and the purified gas leaves from the scrubber.Meanwhile,the acidified droplets in the spray zone are collected into the oxidization zone,which provides sufficient residence time of slurry for the rate-determining reactions including CaCO3dissolution,S(IV)oxidization and CaSO4·2H2O crystallization[10,17].Clearly,the kernel to design,scale up and optimize the WFGD scrubber is to fully understand the SO2absorption into alkaline solution accompanying with the complicated mass transfer between flue gas and slurry droplets in the spray zone.

A single slurry droplet is the essential unit of SO2absorption in the spray zone.For the pure physical absorption,the mass-transfer resistance within a droplet comes from both gas and liquid sides according to classical two-film theory.The gas-side resistance is commonly evaluated by Frössling correlation in the spray scrubber[15,17],while the liquid-side mass transfer resistance,however,is affected by the complex droplet hydrodynamics,such as internal circulation and oscillation.The original penetration theory proposed by Higbie is much more suitable for estimating the mass-transfer resistance in a stagnant droplet[18].On the assumption that the droplet contents could be wellmixed during oscillation,a generalized penetration theory proposed by Angelo et al.[19],called as the surface-stretch model,was verified with the experimental data[20],which was widely employed to estimate the physical mass-transfer coefficient in liquid side during absorption process [10,21–23].For the SO2absorption by alkaline solution within a droplet,the mass transfer of SO2from gas to liquid is coupled with the dissociation of dissolved SO2,which can be considered as instantaneous equilibrium reactions[14,23,24].Accordingly,the above reactions remain totally in the liquid film,with the result that the overall absorption rate is limited by mass transfer process[13,25].

Taking the WFGD scrubber as a unit operation,the one-dimensional axial dispersion model has been used to predict the overall SO2absorption process.Based on the SO2absorption into a single droplet of limestone slurry,Brogren and Karlsson [17]proposed a process model of the spray zone including both instantaneous equilibriums and finite-rate reactions and found the SO2mass transfer was largely liquid-side controlled.Kiil and his colleagues [8,26,27]proposed their process model for describing the rate-determining steps in a pilot-scale falling film absorber and obtained the profiles of gaseous SO2concentration as well as the effect of HCl and organic acid buffers on the desulfurization efficiency.To optimize the industrial desulfurization process,many researchers [11,14,21–24]have developed various models and elucidated the effect of process parameters,such as gas velocity,droplet size,liquid-to-gas ratio,pH value,initial SO2concentration and spraying mode,on the SO2removal efficiency of WFGD scrubber.However,the one-dimensional axial dispersion model is insufficient to represent the scaledependency of complicated fluid dynamic phenomenon in largescale devices [13,28],such as the uneven distribution of gas-slurry flow originating from the lateral inlet of flue gas in the WFGD tower[5].

With the development of computer technology and numerical method,Computational Fluid Dynamics(CFD)has become an effective approach to consider the SO2absorption by droplets coupled with the transport of mass,momentum and energy between flue gas and slurry phases[16,29].The CFD modeling for gas–liquid flow in spray scrubber is generally divided into Eulerian–Eulerian(E–E)and Eulerian–Lagrangian(E-L)approaches,where the difference is based on the treatment method for droplet movement.The former adopts a continuum description of liquid phase,which is thus governed by a set of Navier–Stokes equations[4,10,30],while the later considers the liquid phase as a collection of a discrete number of droplets obeyed Newton's second law of motion.For the gas-slurry flow in the spray zone,the E-L model is more suitable for describing the discrete flow characteristics of slurry droplets in detail[16,29,31].On the one hand,several investigations[16,32–35]qualitatively analyzed the two-phase flow field of flue gas and slurry droplets for predicting the overall SO2absorption performance of WFGD spray scrubber.Montanes et al.[32]suggested the synergistic rings could improve an overall absorption performance of 4%for the WFGD scrubber of 350 MW coal-fired power unit.Chen et al.[33]pointed out the deflectors increased the removal efficiency from 89.6%to 96.7%in the scrubber of 660 MW unit based on the model validated by a pilot-scale device.Qin et al.[34]obtained the gas–liquid distribution and the effect of operation condition and structural parameter on the SO2removal efficiency in the dual-loop spray scrubber of 200 MW coal-fired unit.These works concentrated on the influence of geometrical structure on the overall SO2removal efficiency of industrial-scale device,consequently the reactions in slurry phase are ignored or somewhat simplified,which cannot accurately predict the evolution of chemical properties such as pH value in slurry droplet.Marocco and Inzoli[16]established a comprehensive model considering the multiphase hydrodynamics,H2O evaporation and SO2absorption coupled with the thermodynamics of aqueous chemistry,which was used to predict the overall SO2removal efficiency validated against the measured data in a pilot-scale reactor.Later,Marocco[35]illustrated the impact of spray layer combination mode on the absorption performance of an industrial desulfurization unit.On the other hand,only a few studies[7,30,36]concerned about the uniformity of gas and droplets in the scrubber.Zhang et al.[7]quantitatively described the uniformity of gas flow by the coefficient of maldistribution in a full-scale scrubber.Wang et al.[30,36]theoretically proposed the“droplet self-adjustment”effect in order to explain the flow distribution mechanism of gas and droplets in the spray scrubber.Noted the above investigations[7,30,36]ignored the SO2chemical absorption for simulating the gas–liquid transfer process.

To the best of our knowledge,there exist few studies explained the dependence of intricate absorption-reaction phenomena on the non-ideal contacting patterns in full-scale WFGD scrubbers.In order to obtain a deeper insight into commercial desulfurization process,a detailed evolution for gas-slurry hydrodynamics and SO2chemical absorption needs to be paid more attention in different regions of the spray zone.The aim of this paper is to better understand the desulfurization performance of industrial-scale unit based on the fundamental relationship between transport process and chemical reactions of gas-slurry two-phase flow.A comprehensive CFD model is established by involving inter-phase momentum exchange,heat transfer,H2O evaporation and SO2absorption combined with reactions in slurry phase,which is validated by the measured data from a WFGD scrubber of 330 MW coal-fired power unit.Three regions are distinguished in terms of the unique characteristics of each gas-slurry flow pattern,which is expanded to grasp the dependence of SO2absorption performance on the complicated hydrodynamics of two phases in WFGD scrubber.

2.CFD Modeling and Computational Procedure

A comprehensive CFD model is established by considering the chemical reactions and transfer phenomena between flue gas and slurry droplets in the WFGD spray scrubber.To balance the accuracy of engineering application and effort of computation,the main assumptions are described as follows[11,16,32–35]:

(1) The rate-determining reactions are ignored in the absorption process;

(2) All chemical reactions involved are assumed to be in equilibrium instantaneously;

(3) Each droplet is treated as a non-rotary rigid sphere;

(4) The collision and coalescence between droplets are neglected;

(5) CO2absorption process into droplet is ignored.

2.1.Chemical reactions in SO2 absorption process

The chemical reaction model for describing SO2absorption process is established to predict the concentrations of main dissolved species in slurry phase.Assuming that the gaseous species are chemically inert,all the reactions associated with SO2absorption take place in the aqueous phase[11,21].Moreover,based on Assumptions(1)and(2),the kinetic controlled reactions including S(IV) species oxidation,CaCO3dissolution and CaSO4·2H2O crystallization can be neglected due to the relatively short residence time of slurry droplet in the spray scrubber[15,16,24].Accordingly,six equilibriums are consisted in the chemical reaction model as below:

In this model,the dissolved species taken into account are H+,OH−,SO2,aq,,Ca2+,Mg2+and Cl−,among of which the concentrations of Ca2+,Mg2+and Cl−are regarded as constants[5,8,26],while the others are determined by the chemical equilibriums combined with the balances of mass and electric charge[15–17,22].Table 1 summarizes the acid–base equilibrium constants for Eqs.(2)to(7),where[X]represents the molar concentration of dissolved compound X,and Tdis the temperature of slurry droplet.

Following Zhu et al.[15]and Warych and Szymanowski [22],the mass balances of S(IV),S(VI)and carbonate species are obtained by:

where NSO2is the molar flux of SO2from gas bulk to droplet,which will be discussed in Section 2.3.3.

The charge balance reflects the electroneutrality of all ions in slurry droplet[4,16,35],which is expressed as:

During CFD simulation,the concentrations of dissolved species in each time step are calculated by Eqs.(2)to(11),which form a set of non-linear algebraic equations.To determine the initial condition of slurry injection,the dissolution equilibrium of CaCO3and electroneutrality of ions in the oxidation zone are considered,which is represented by the following auxiliary reaction system[16]:

where KCaCO3is taken from Plummer and Busenberg[38].

2.2.Governing equations for gas-slurry flow

The Eulerian–Lagrangian framework is employed to simulate the multiphase transfer phenomena and chemical reactions,where flue gas and slurry droplets are treated as the continuous phase and discrete phase,respectively.

2.2.1.Continuous phase(flue gas)

The Eulerian approach is used to account for the conservation laws of flue gas,which is considered as a perfect mixture composed of SO2,H2O vapor and inert species,i.e.,N2,O2and CO2.The governing equations for mass,momentum,energy and local mass fractions of gaseous species are written as follows:

Table 1 Acid–base equilibriums in the chemical reaction model

where the subscripts i and j stand for the Einstein notations to denote the spatial directions.The source terms Smass,Smomand Senare the contributions of the mass-,momentum-and energy-transfer between flue gas and slurry droplets,respectively,which will be discussed in Section 2.3.

For a fully specified set of equations,the closure laws are required for fluid viscous stress.Based on the assumption of Newtonian fluid,the stress tensor τ in Eq.(15)is estimated by the following constitutive relation:

where δijis Kronecker delta function(when i=j,δij=1;i ≠j,δij=0),μ represents the dynamic viscosity of flue gas assigned as 1.96×10−5kg·m−1·s−1.

The motion of flue gas is simulated by the Reynolds-averaged equations,in which the Realizable k-ε turbulence model is adopted to solve Reynolds stresses.The transport equations for turbulence energy k and dissipation rate ε are expressed as:

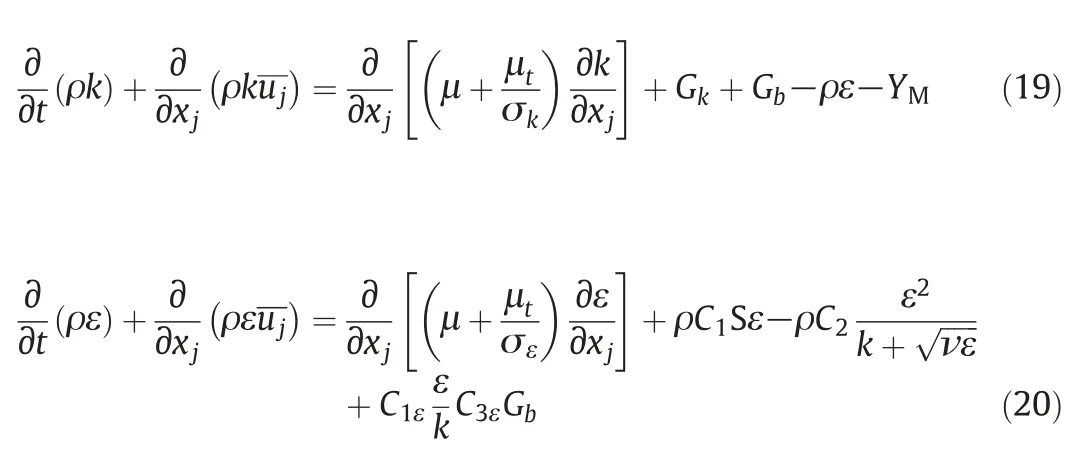
The details of model coefficients in Eqs.(19)and(20)are referred to Shih et al.[39].

2.2.2.Dispersed phase(slurry droplets)

The Lagrangian approach is used to describe the motion of slurry droplets,which are considered as the homogeneous mixture mainly including water and dissolved SO2(SO2,aq)according to Assumption(1)that the rate-determining reactions are ignored in absorption process.The histories of physical and chemical quantities in slurry droplets are solved by Discrete Phase Model (DPM) [31,40].For a single droplet,the equation of motion relating droplet velocityto trajectoryis defined as below:

The governing equations of force,energy and mass for the droplet i are formulated as[31,33]:

where mdand cddenote the mass and specific heat of slurry droplet,respectively.

2.3.Transfer behaviors between gas phase and slurry droplets

In order to close the governing equations in Section 2.2,the transfer behaviors between flue gas and slurry droplets in the spray scrubber are obtained as the following sections.

2.3.1.Momentum transfer

For the forces acting on droplet in the spray zone,it is appropriate that only the drag force is considered in the solution of gas-slurry momentum exchange [30,41,42].Accordingly,the momentum source term of each droplet in Eq.(22)becomes:

where CDis the drag coefficient depended primarily on the Reynolds number for droplet,which is evaluated by the correlation from Morsi and Alexander[43]:

where a1,a2and a3are constants depending on the range of Reynolds number,and Reddenotes the Reynolds number based on the droplet diameter (dp) and the slip velocity between gas and slurry dropletwhich is defined as:

2.3.2.Heat transfer

The gas-slurry energy exchange mainly comes from the convective and latent heat transfer[16,32].The former is related to the temperature difference between the bulk of flue gas and surface of droplet,whilst the latter is governed by the pressure gradient of H2O vapor.For a single droplet,the source term associated with heat transfer process is given as:

where λ and Pr represent the thermal conductivity and Prandtl number of flue gas,respectively.

2.3.3.Mass transfer

Both SO2absorption and H2O evaporation are considered in the mass transfer between flue gas and slurry droplets.The source term in Eq.(24)is expressed as below:

For the H2O evaporation process,the Stefan flow can be ignored due to the slow evaporation rate of droplet in the spray scrubber[21,32].Thus,the evaporation rate of H2O for the droplet i is formulated as:

where Sc is the Schmidt number expressed as Sc=μ/ρ,and DH2O,gis the binary diffusion coefficient in gaseous mixture evaluated with the empirical correlation by Fuller et al.[46]:

For the SO2chemical absorption process,the hydrolysis and dissociation reactions of dissolved species are assumed in equilibrium state throughout the droplet[21–24].As shown in Fig.2,the mass-transfer resistance in the layers of gas and slurry droplet is dominant in SO2chemical absorption process,because the resistance from the kineticcontrolled reactions in liquid bulk can be neglected[14,33].Accordingly,the absorption rate of SO2from gas bulk to droplet i is calculated as:

where E is the enhancement factor characterized the reinforcement effect of above reactions compared to physical mass transfer [13,25],which is referred to Brogren and Karlsson [17]and Warych and Szymanowski[22],is the Henry's constant for SO2calculated by the correlation of Maurer [37],andcorrespond to the mass-transfer coefficients in gas and liquid sides,respectively.

The mass-transfer coefficient of SO2in the bulk of flue gasis determined by the following correlation[22,24,44]:

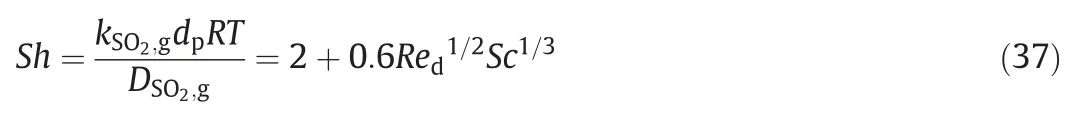
As to the mass-transfer coefficient in liquid side,is obtained from the surface stretch model developed by Hsu and Shih[20]:

Fig.2.Schematic of two-resistance theory for SO2 absorption process.

where α is the correction factor assigned as 0.78,is the diffusion coefficient of SO2in liquid side evaluated by Newton et al.[47],and σd-gis the surface tension of droplet referred to Desch et al.[48]:

2.4.Numerical strategy for simulating chemical reactions and gas-slurry transfer behaviors

As illustrated in Fig.3,the inter-phase coupling method is employed to simulate the transfer behaviors of momentum,heat,and mass between flue gas and slurry droplets,and chemical reactions in aqueous phase.The detailed strategy is as follows:

(1) The flow field of flue gas is solved in the Eulerian framework by Eqs.(14)to(20);

(2) In the obtained flow field of flue gas,the physical quantities of slurry droplets are calculated by Eqs.(21)to(24)through tracking the finite number of representative trajectories in the Lagrangian framework,called parcels[31,40];

(3) The source terms in the governing equations are determined by Eqs.(25) to (40),meanwhile the set of non-linear algebraic equations for the chemical reaction model comprised of Eqs.(2) to (13) is activated to evaluate the concentrations of dissolved species in slurry droplet;

(4) The gas flow field is acquired again considering the counteractions from the slurry droplets.Then the histories of droplet parameters and the gas flow field are solved alternately with the continuously updated source terms.

The calculation of gas-slurry transfer behaviors is accomplished until the iterations entirely reach the convergence criterions.In order to verify the convergence of CFD solution,the desulfurization efficiency η and pressure drop ΔP in the spray scrubber are monitored during each iteration.In the view of engineering application,the solution is supposed to be converged when η and ΔP vary lower than 0.1% and 20 Pa,respectively.

All numerical simulations are conducted using the commercial CFD solver in a platform of Intel 2.60 GHz Xeon with 32 GB RAM.The models describing the chemical reactions and gas-slurry transfer behaviors in the spray scrubber are coded into a set of user defined subroutines to update the chemistry compounds mentioned in Section 2.1 and the source terms in Section 2.3.In the Eulerian framework for flue gas,the velocity–pressure coupling SIMPLE-Consistent algorithm is employed to solve the finite-volume differential equations,and the spatial discretization scheme for the convective terms is the second order upwind.In the Lagrangian framework for slurry droplets,the physical time step of DPM calculation is prescribed as 20 mm in the length scale for integrating the ordinary differential equations based on sensitivity analysis.

3.SO2 Absorption Performance in a Scrubber of 330 MW Coal-fired Power Unit

In order to predict the desulfurization process using the CFD model for both chemical reactions and gas-slurry transfer behaviors,the numerical error is evaluated based on sensitivity analysis,and this model is validated by using the measured data from an industrial-scale spray scrubber.

Fig.3.Diagram of inter-phase coupling method.

Fig.4.Schematic of computational domain and layout of nozzle arrays.

3.1.Geometric configuration and process parameters

Fig.4a shows the industrial-scale WFGD spray scrubber of 34.85 m height with a diameter of 13.1 m,which is in operation from a 330-MW(e) coal-fired power unit established in Shanxi province,China.This WFGD system has a desulfurization capacity for 1.25 × 106m3·h−1of flue gas on dry basis.The geometric configuration of scrubber and process parameters under the design condition are listed in Tables 2 and 3,respectively.

Since the key issue of this study is to further understand the SO2absorption process in the WFGD scrubber,the spray zone is simulated extensively compared with the mist eliminator(ME)in the demist zonetreated as a porous block and the free surface in the oxidation zone set as the bottom of scrubber.The computational domain is depicted in Fig.4b,where the bottom of scrubber locates in the plane of z=0.The lowest spray layer,denoted as spray layer 1st,has a 9.75 m clearance to the bottom.Fig.4c exhibits the layout of nozzle arrays from the top view.There are 125 swirl atomizing nozzles installed in each spray layer,which are single-orifice (−z direction) under the main pipe and near the wall,whilst the dual-orifice nozzles(−z and+z directions)are in the rest area.The ME is considered as a perfect collector for the slurry phase,which means that no droplet is entrained by flue gas above the ME.

Table 2 Geometric configuration of WFGD scrubber

Table 3 Process parameters of WFGD scrubber under the design condition

3.2.Initial and boundary conditions

To initialize the chemical reaction model in Section 2.1,[H+]0,[Mg2+]0,[Cl−]0andin slurry are obtained by measuring the samples withdrawn from the oxidation zone[8].Herein the subscript 0 denotes initial state.The measured data are listed in Table 3,where[H+]0is obtained by the pH meter (PHBJ-260,Leici,China),and[Mg2+]0,[Cl−]0andare determined through the titration method using EDTA,AgNO3and BaCl2,respectively.Then[OH−]0andare estimated by Eqs.(2) and (5),respectively.Under the forced oxidation condition,almost all S(IV)species convert into S(VI)ones in the oxidation zone [4,22,24],as a result,[SO2,aq]0,andare assigned as 0.Besides,[CO2,aq]0,and [Ca2+]0are calculated by Eqs.(6) and (7) combined with Eqs.(12)and(13).

Flue gas enters the spray scrubber from the Mass Flow Inlet with uniform velocity,where the turbulent kinetics energy and turbulent dissipation rate of inflow are estimated by the empirical correlations[30].Purified gas outlet is prescribed as the Pressure Outlet with the operating pressure of 0.1 MPa.No-slip and adiabatic wall condition is imposed to the inner walls and the surfaces of pipelines and synergistic rings.

Slurry droplets are discharged from the spray nozzles at a 90°conical angle.The boundary conditions(BC)for droplets are set as“escape”at the inlet and bottom of scrubber,where the tracked parcels are excluded from further calculation.Following Weiss and Wieltsch [29]and Marocco[35],the ideal elastic reflection BC is assigned at the internal surfaces to predict the droplet-wall interaction.The size distributions of poly-dispersed streams are represented by 10 discrete diameters from 0.5 mm to 5 mm at equally spaced intervals.Rosin-Rammler model is employed to describe the size distribution of slurry droplets as below[45]:

where Y(dp)is the cumulative mass fraction of droplets with diameters greater than dp,deis the size constant and n is the spread parameter.deand n are respectively assigned as 2.5 mm and 3.0 in this study.

3.3.Sensitivity analysis

To simulate WFGD spray scrubber using Eulerian–Lagrangian approach,numerical results are supposed to be more accurate by using higher grid resolution in the Eulerian frame and more representative trajectories in the Lagrangian frame.However,the expensive effort is required during the calculation[40,49].To obtain a numerical solution independent from the numbers of cells and parcels,the sensitivity analysis is conducted based on desulfurization efficiency η and pressure drop ΔP selected as the indicators.

Fig.5.Schematic of geometry discretization with different sizes of tetrahedral cells.

Fig.6.Performance parameters of scrubber depending on number of cells.

The computational domain is discretized with tetrahedral cells as shown in Fig.5.Flue gas is supposed to be forced to rapidly turn and accelerate in the vicinity of pipelines and synergistic rings,where the grid system is further refined to more accurately capture the information in flow field.Five grid systems are yielded with the number of tetrahedral cells from 0.95 million to 3.9 million.As shown in Fig.6,η varies below 0.1%and ΔP changes lower than 20 Pa when the number of cells is more than 2.4 million.To get a tradeoff between the calculation accuracy and computational effort,the grid system with 2.4 million cells is used in the following simulations.

Fig.7 displays the sensitivity of numerical solution toward the variation of parcel numbers for each nozzle(Np).Both η and ΔP increase when Npis lower than 200,which indicates that the number of parcels is not enough to meet with a reasonable statistical error for the interaction between two phases[40,49].In the range of Npfrom 200 to 800,however,η and ΔP vary lower than 0.1%and 20 Pa,respectively.Accordingly,the solution of Np=200 is acceptable under the design condition in Table 3,corresponding to the total number of 105parcels in the whole scrubber.

Fig.7.Performance parameters of scrubber depending on parcel numbers.

Fig.8.Comparison of measured and simulated desulfurization efficiencies for the WFGD scrubber in a 330 MW coal-fired unit.

3.4.Model validation

To validate the CFD model describing chemical reactions coupled with gas-slurry transfer behaviors,desulfurization efficiencies are predicted by compared to the corresponding measured data from the spray scrubber in Section 3.1.Fig.8 shows the desulfurization efficiency gradually declines with the increase of inlet SO2concentration cSO2,in,which is consistent with Neveux and Moullec [11]and Zhong et al.[14].The predicted desulfurization efficiencies are higher than the measured values,yet the deviation of η is lower than 1%,manifesting that the CFD model is credible to simulate the complex reactions together with gas-slurry transfer behaviors in the industrial device with an acceptable accuracy.

4.Results and Discussion

Based on the validated CFD model,the gas-slurry flow patterns are studied in different regions within a full-scale WFGD scrubber.Then chemical reactions and gas-slurry transfer behaviors are explored based on the region identification to obtain a better understanding of industrial desulfurization process.

4.1.Region identification based on gas-slurry flow pattern

Under the operational condition presented in Table 3,the profiles of gas velocity and slurry concentration are shown in Fig.9.The velocity of raw gas from the inlet gradually decreases when gas contacts with slurry droplets(Fig.9a).Above the inlet of flue gas,e.g.the plane of z=8.5 m,the gas-flow“channeling”with high velocity still appears around the wall with low slurry concentration.With the further increase of elevation,the velocity of gas channeling decreases ascribed to the modification from the falling droplets and synergistic rings[32,33],which can be observed in the plane of z=12.5 m or z=16.5 m.As presented in Fig.9b,slurry phase is dilute around the inlet due to the impaction of high-speed gas flow,which is also observed experimentally by Chen et al.[33].The region from the inlet to the spray layer 1st contains almost all falling droplets,resulting in higher slurry concentration in the cross section.Above the spray layer 1st,however,slurry concentration decreases obviously with the increase of scrubber height(e.g.from the plane of z=11.5 m to z=14.5 m),because the droplets are merely provided by the upper spray layers.It should be stressed that slurry phase is in very low concentration when the scrubber height is higher than 16.5 m.Herein droplets fulfill the re-entrainment criterion and their corresponding gas-slurry slip velocitiesare close to 0,where the transfer intensity between two phases is rather weak[42].As a result,the following discussion focuses on the transfer behaviors and reactions from the height of 0 to 16.5 m,which can be defined as the spray zone in this scrubber.

Fig.9.Distributions of(a)gas velocity and(b)slurry concentration in spray scrubber.

The motion of two phases is determined by the interaction between flue gas and slurry droplets.Falling in the upward plug flow of flue gas,spray droplets are supposed to attain the terminal velocity immediately in a typical counter-current mode[11,30,41].The force balance for a single droplet can be derived from Eqs.(22)and(25):

In an actual WFGD scrubber,however,slurry droplets are no longer in the force-balanced state in Eq.(42),mainly because the gas-slurry contacting pattern always deviates from the ideal counter-current mode[11,13].To clarify the two-phase flow pattern within the scrubber,three regions are distinguished in terms of gas-slurry flow structures represented by the velocity vector of flue gas in Fig.10 and the axial velocity distribution of slurry droplets in Fig.11.

In the Region I from the height of 0 to 6.5 m,raw gas tends to traverse through the scrubber in the lateral direction(see Fig.10).Then 3-D vortices with complex hydrodynamic structures are formed due to the interaction between two phases.For slurry phase in Fig.11,a certain number of droplet trajectories deflect from the vertical direction influenced by raw gas.Owing to the direction change of flue gas,the droplet velocity(ud)increases gradually until force-balanced state is achieved again.A remarkable feature in this region is the presence of flue gas vortices.

In the Region II from the height of 6.5 to 9.75 m,the lateral direction of gas flow gradually turns to upward because of adequate drag force from slurry phase[7],while droplets move downwards and their corresponding velocities slightly fluctuate during the falling process,implying that these droplets are approximately in the force-balanced state[11,30,41].Clearly,this region is dominated by the counter-current condition.

In the Region III from the height of 9.75 to 16.5 m,the bias gas flow is formed when flue gas upwards passes through the synergistic rings and pipelines.Nevertheless,the maldistribution of gas phase can be mitigated by slurry injections right away.For slurry phase,a certain number of droplets move upwards from the dual-orifice nozzles,leading to the local co-current mode in this region.Furthermore,the proportion of droplets in the force-balanced state decreases with the increase of scrubber height because more droplets are still in the initial stage of spray[36].It is proposed that the gas-slurry flow pattern in this region is significantly influenced by the morphology and direction of slurry injection.

Fig.10.Schematic of gas flow structure and vector of flue gas.

Fig.11.Schematic of slurry flow structure and axial velocity distribution of droplets.

4.2.Uniformity characteristics of gas-slurry distribution

Relative Standard Derivation(RSD)is introduced to investigate the uniformity degree of gas-slurry flow over the cross section in the spray zone.RSDgfor gas velocity and RSDsfor slurry concentration are defined as[7,30]:

where wgis the vertical velocity of flue gas,csis the slurry concentration,and N is the total number of statistical samples.The subscript m and i denote the mean value and the sample index in the cross section.

Fig.12.Profiles of uniformity degree for gas and slurry along the height of scrubber.

The statistical data of RSDgand RSDsare presented in Fig.12.RSDgin Region I is much higher than that in other two regions because of the backflow from gas vortices.The profile of RSDsimplies more severe maldistribution of slurry because slurry phase is dilute around the inlet of flue gas.The above results indicate that the gas-slurry uniformity degree is largely influenced by flue gas from the inlet in this region.

In Region II,RSDgsharply decreases from 1.06 to 0.37 with the raise of height from 6.5 m to 9.75 m,implying that the uniform degree of gas flow is improved.As to slurry,the profile of RSDspresents a unimodal distribution with a peak close to the spray layer 1st at z=9.75 m,since the droplets from the upper layers could hardly cover the area below the pipelines.RSDsbecomes relatively stable as 0.35 or so and is evidently lower than the corresponding values in other two regions.This finding suggests the uniformity degree of gas flow is determined by the modification originating from the force-balanced droplets in this region.

In Region III,not only the interaction between two phases,the gasslurry distribution is also affected by the pipelines of spray layers.For flue gas,RSDgfirstly decreases from 0.37 to 0.28 with the height of 9.75 m to 12 m,because the modification of uniformity is still dominated by the droplets.Above the elevation of 12 m,however,the uniformity degree slightly deteriorates until flue gas passes through the top spray layer since the effect of droplets is gradually reduced by the perturbation of pipelines.For slurry phase,the profile of RSDspresents a multimodal distribution with the peaks below the corresponding pipelines.Although RSDsfluctuates throughout Region III,the maldistribution of slurry tends to be aggravated with the increase of scrubber height,which is caused by the decreasing proportion of droplets in the force-balanced state and the reduction of slurry coverage area in the cross section.

In general,even though the gas distribution could be disturbed by the pipelines of spray layers,the falling droplets still play a more significant role in gas flow modification.Consequently,the uniformity degree of flue gas in the whole scrubber is mostly modified by the slurry droplets in Region II,which is consisted with Wang and Dai[30,36].However,slurry cannot be evenly sparged into the scrubber largely because the uniformity degree of slurry is restricted by the spray conditions such as the morphology of slurry injection,number of nozzles and layout of nozzle arrays[4].This implies that the more uniform distribution of slurry droplets in Region II is beneficial to improve the uniformity degree of flue gas in the whole scrubber.

4.3.Momentum and heat transfer between flue gas and slurry droplets

The pressure drop of flue gas is one of important performance parameters for the WFGD scrubber relating to the momentum transfer between flue gas and slurry droplets under the counter-current spray mode[30].Theoretically,the pressure drop of gas phase is determined by the sum of drag force originating from slurry droplets,and thus the pressure gradient of flue gas in the poly-dispersed spray system is formulated as[41,42]:

where the subscript i presents the index of droplet group with the same initial diameter.Based on the findings in Section 4.1,the volumetric rate of slurry per unit cross-sectional area(Li)can be treated as a constant in Region I or II.The drag coefficient(CD,i)changes remarkably little in the present scrubber since the Reynolds number for falling droplet is mainly in the range of Red>400[50].

To obtain the characteristics of inter-phase momentum exchange under different gas-slurry contacting patterns within the industrialscale scrubber,both the averaged total pressure and corresponding pressure gradient of flue gas are investigated with different liquid-togas ratios(L/G)in Fig.13.In general,the total pressure decreases monotonically as a function of elevation,whereas the pressure gradient is quite different in three regions.

Fig.13.Profiles of(a)averaged total pressure of flue gas and(b)pressure gradient along the height of scrubber.

In Region I,the total pressure varies slightly in Fig.13a,and its gradient in Fig.13b is much lower than that in Region II.As stated in Section 4.1,a certain number of droplets deviate from the force-balanced state due to the gas vortices existing in this region.The backflow of flue gas reduces the magnitude of slip velocity between two phasesMoreover,the droplet velocity(ud)increases during its falling process,while slurry holdup decreases mirrored by the raise of ud[41].In agreement with Eq.(45),the decreasingand increasing udgives rise to a lower flow resistance for flue gas.In Region II,the total pressure sharply decreases in the linear relationship with the elevation and presents the synchronicity with the evolution of RSDgin Section 4.2.Correspondingly,the pressure gradient is more stable and much higher than that in other two regions.It qualitatively suggests that Region II is operated in an approximate counter-current mode.In Region III,the total pressure eventually achieves a stable state and the corresponding gradient decreases in the axial direction,indicating that the momentum transfer between two phases is weakened gradually.The primary reason may be the decline of slurry flow rate Liwith increasing the elevation of scrubber as mentioned in Section 4.1.Besides,more slurry droplets are still in the initial stage of injection with the increase of elevation,leading to the decrease ofwhich is another reason for the reduction of pressure gradient.

As shown in Fig.14,the evident gradients for both gas temperature and H2O vapor concentration merely appear around the inlet of flue gas,and flue gas is cooled down and saturated with H2O soon below the spray layer 1st.It can be inferred that SO2absorption performance and gas-slurry flow pattern are less affected by the heat transfer combined with H2O evaporation in the spray zone,which coincides with Marocco and Inzoli [16]and Montanes et al.[32].For this reason,many researches[4,30,33–36]neglected the variation of temperature or moisture content for flue gas in their CFD simulations of desulfurization processes,which were based on the assumption of incompressible flow.Although these models could predict the hydrodynamics or absorption performance for the scrubbers to some extent,either the density of flue gas or the evolution of droplet size could not be represented accurately.

Fig.14.Distributions of(a)temperature and(b)relative humidity for flue gas in three regions.

4.4.SO2 chemical absorption process

According to the operational parameters listed in Table 3,the SO2concentration in flue gas and pH distribution in slurry droplets are exhibited in Fig.15.Intuitively,SO2concentration declines with the increase of scrubber height in Fig.15a,while the higher concentration presents around the inlet ascribed to the bias flow of flue gas,which is consistent with Qin et al.[34].Correspondingly,the overall pH in slurry phase decreases during the falling process in Fig.15b as a result of the SO2dissolution in aqueous phase[8,21–23].

To obtain a comprehensive insight into the chemical absorption process in an industrial-scale apparatus,the evolution of SO2mass transfer together with chemical reactions in aqueous phase is investigated in the above three regions.Fig.16 summarizes averaged SO2concentration and the corresponding gradient along the height of scrubber.The profile of averaged pH value in slurry phase is presented in Fig.17.It can be found that SO2concentration is close to 0 and the pH level of entrained droplets cuts down to about 3.8–4.2 when the elevation is higher than 16.5 m above the spray zone.As a result,SO2concentration gradient tends to 0 in this pneumatic conveying condition.It quantitatively demonstrates SO2absorption process is almost completed in the spray zone.

Fig.17.Profile of averaged pH value in slurry phase along the height of scrubber.

Fig.15.Distributions of(a)SO2 concentration in flue gas and(b)pH value in slurry droplet under the design condition.

Fig.16.Profiles of(a)averaged SO2 concentration in gas phase and(b)concentration gradient along the height of scrubber.

In Region I,the SO2concentration declines when the height decreases from 6.5 m to 0 in Fig.16a due to the relatively long residence time of gas vortices.However,the pH in slurry phase decreases into a steady state without significant dissolution of S(IV)species as shown in Fig.17,which is similar to Kiil et al.[8]and Brogren and Karlsson[17].In agreement with Eqs.(34)and(35),a weakened chemical reinforcement together with a decreased absorption driving force leads to a lower SO2concentration gradient in Fig.16b,which is proportional to SO2mass transfer rate.Combined with the uniformity analysis of gas-slurry distribution in Region I as discussed in Section 4.2,the contacting pattern of two phases and distribution of SO2concentration are largely affected by the hydrodynamics of raw gas from the inlet.Hence,Region I can be defined as Gas Inlet Region(GIR).

In Region II,similarly to the corresponding profile of total pressure in Fig.13a,SO2concentration declines sharply in an almost linear relationship with increasing elevation in Fig.16a,which manifests an intensive transport condition for SO2and elucidates the synchronicity with momentum transfer process.As shown in Fig.17,the pH value in slurry phase decreases by about 0.5 during the droplet falling process due to the dissolution of S(IV)species and rapid accumulation of H+,leading to the decline of mass-transfer coefficient in liquid side[11,17].In conclusion,the chemical absorption of SO2mainly occurs in Region II,which is attributed to both the sufficient gas-slurry interface and significant mass-transfer driving force in the counter-current condition.Therefore,Region II can be designated as Dominant Absorption Region(DAR).

In Region III,the droplet pH maintains about 4.5 to 5.2.This stable and high pH level in slurry phase gives rise to greater chemical reinforcement and higher absorption capacity compared to those in Region II(DAR).However,SO2concentration gradient drops off precipitously in Fig.16b,which is largely due to the decreasing gas-slurry interfacial related to slurry flow rate(Li)in Section 4.3 and the reducing absorption driving force in Fig.16a.In a word,the droplets close to nozzles have better absorption performance,whereas the spray layers are most likely to provide fresh absorbent for Region II.Accordingly,Region III can be named as Slurry Dispersed Region(SDR).

In summary,the gas-slurry contacting pattern in Region II(DAR)is dominated by the counter-current mode with large amount of forcebalanced slurry droplets,which is more favorable to SO2absorption compared to other two regions.However,the contacting pattern between flue gas and slurry droplets is affected by the lateral raw gas in Region I(GIR)and the spray conditions in Region III(SDR)as mentioned in Section 4.1,these two regions provide the initial conditions of transfer process and chemical reactions in DAR.Accordingly,the overall desulfurization performance of WFGD scrubber is directly affected by the uniformity degree of gas-slurry two phases in DAR,which is more or less resulted from the complicated hydrodynamics in both GIR and SDR.

5.Conclusions

Based upon the Eulerian–Lagrangian framework,the chemical reactions associated with SO2absorption process and other gas-slurry transfer phenomena are investigated in an industrial-scale WFGD spray scrubber.Flow regions are identified to explore the dependence of desulfurization performance on inter-phase transfer behaviors between two phases in the spray zone.The main results are as follows:

(1) The CFD modeling for chemical reactions and gas-slurry transfer behaviors is validated by the operational data of desulfurization efficiency from a WFGD scrubber of 330 MW(e) coal-fired power unit.

(2) Three regions are identified based on the flow pattern of gas and slurry phases.The feature of Region I in the lower part of scrubber is the presence of flue gas vortices influenced by the hydrodynamics of raw gas,Region II in the middle part of scrubber is dominated by counter-current mode due to the droplets approximately in force-balanced state,and the gas-slurry flow pattern in the upper part of scrubber(Region III)is significantly influenced by spray conditions.

(3) Falling droplets play the most significant role in gas flow modification,and the overall uniformity degree of flue gas in scrubber is mainly determined by the droplets in the middle part of scrubber(Region II).It suggests that the improved slurry distribution in this region is beneficial to promote the uniformity degree of flue gas in the whole scrubber since slurry cannot be evenly sparged into the scrubber restricted by spray conditions.

(4) The behaviors of inter-phase momentum exchange and SO2transfer associated with acid–base reactions present the synchronicity in three regions in dependence of the corresponding gas-slurry flow patterns.Comparatively,the heat transfer combined with H2O evaporation merely appear around the inlet of flue gas,which less affects the desulfurization performance and gas-slurry hydrodynamics in the spray zone.

(5) Three regions are identified as Gas Inlet Region(GIR),Dominant Absorption Region (DAR) and Slurry Dispersed Region (SDR)from the bottom to top of scrubber.The evolution of hydrodynamic structure in GIR or SDR provides the initial conditions of transfer process and chemical reactions in DAR.However,the overall desulfurization efficiency of WFGD scrubber is determined by the absorption conditions in DAR with more intensive interactions between two phases compared to other two regions.

Nomenclature

ADprojected area of droplet,m2

Adsurface area of droplet,m2

CDdrag coefficient

cdspecific heat of droplet,kJ·kg−1·°C−1

Dkdiffusion coefficient,m2·s−1

dpdiameter of droplet,m

E enhancement factor

e internal energy per unit mass,kJ·kg−1

g acceleration of gravity,m·s−2

H Henry's constant,Pa·m3·kmol−1

h convective heat transfer coefficient,W·m−2·°C−1

hksensible enthalpy of gaseous species k,kJ·kg−1

Jkdiffusion flux of gaseous species k,kg·m−2·s−1

Kiequilibrium constant of dissolved species i

Ktotoverall mass-transfer coefficient,kmol·m−2·s−1·Pa−1

kgmass-transfer coefficient in gas side,kmol·m−2·s−1·Pa−1

keffeffective conductivity,W·m−1·°C−1

klmass-transfer coefficient in liquid side,m·s−1

L volumetric rate of droplet per unit cross-sectional area,m3·m−2·s−1

mdmass of droplet,kg

Npnumber of tracked parcels from each nozzle

Pipartial pressure of gaseous species i,Pa

p static pressure of fluid,Pa

R universal gas constant,kJ·kmol−1·°C−1

T temperature,°C

u velocity,m·s−1

ε turbulence energy dissipation rate,m2·s−2

η desulfurization efficiency,%

μ dynamic viscosity of flue gas,kg·m−1·s−1

ρ density,kg·m−3

σd-gsurface tension of droplet,N·m−1

τ shear stress,kg·m−1·s−2

ωimass fraction of gaseous species i

Subscripts

d droplet

g gas phase

l liquid phase

0 initial value

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (51706070 and U1910215),and the Fundamental Research Funds for the Central Universities(2018ZD03,2020MS008 and 2020MS078).