张晓闻, 任勇峰

(中北大学仪器与电子学院， 太原 030051)

粒子群算法(particle swarm optimization, PSO)[1]是一种模拟鸟群觅食行为的优化算法，近年来，由于该算法简单，参数设置少，容易跳出局部最优，搜索到全局解被广泛应用。传统粒子群算法为不同的交互对象构造两种不同的版本，全局最好模型(globalbest，Gbest)及局部最好模型(localbest，Lbest)。而近年来，学者们研究了很多不同的改进算法，文献[2]中以Shi和Eberhart的粒子多样性为基础，给出了多种求解位置多样性、速度多样性及种群多样性的方法，都取得了很好的效果。其他方面，文献[3]中提出一种融合优质粒子分布的粒子群优化算法，在“社会”部分加入以分布估计算法为基础的优质粒子，该优质粒子是根据统计学习概率模型而产生的。文献[4]为了在扩大粒子搜索空间时避免陷入局部最优，利用了正弦函数独有的振动特性，在位置公式中加入正弦三角函数因子。有的学者根据反推理论，从反向学习的角度出发，文献[5]利用反向学习策略进行改进，用反向解代替当前解，择优进行下一次迭代。文献[6]在反向学习的基础上，引入折射原理思想，对粒子群算法进行改进。还有研究学者利用小生境邻域[7]的思想进行改进粒子群算法，其思想是粒子的邻域结构随着迭代次数的变化而变化。因此针对不同的问题提出适合该问题的邻域结构，如文献[8]提出了利用拓扑结构构造局部邻域解。文献[9]提出了一种带有粒子聚合度的改进粒子群算法，该算法中融合了聚合度和惯性权重的概念，聚合度反映粒子聚集的程度，作用是使粒子跳出局部最优。文献[10]针对PSO算法的不确定动态多目标优化问题，在位置更新公式中引入动态变异算子，通过分段线性函数参数化实现不确定动态多目标优化。文献[11]通过历史数据学习模型避免算法陷入局部最优。文献[12-14]通过聚类模型和自适应模型改进算法，从而实现算法的收敛速度和搜索精度的平衡。

在以上改进算法中，都忽略了一个问题，无论学习机制、拓扑结构、引入算子模型及邻域思想如何等，只是将各项学习之间看作相互独立的个体，都忽略了学习机制之间的关系。为了使粒子的多样性得到进一步利用，避免粒子群体过早收敛，现在树状拓扑结构的基础上，将空间中的粒子利用拓扑结构分类，得到局部最优解，利用四元数理论，将3种学习机制：自身最优、全局最优和局部最优作为四元数的3个虚部向量，将四元数项作为相关项信息加入到粒子群算法中，用于调节3种记忆粒子之间的相互关系。粒子群算法的应用广泛，可用于信号处理、图像处理、滤波器等多个领域。

1 相关理论

1.1 树状拓扑结构

文献[15]提出一种逐级寻优拓扑结构(Tree-PSO，TPSO)，主要是一种基于树状的拓扑结构，如图1所示，该结构中由子节点之间交流比较，得到上一层父节点，直到找到全局最优值。

图1 TPSO拓扑结构及节点分布Fig.1 TPSO topology and node distribution

1.2 四元数理论

四元数[16]是一个表示超复数的数学概念，它的构成是实部加上3个虚部单位i、j、k。每个四元数都可由1、i、j、k线性表出，则四元数的一般表达式为q=a+bi+cj+dk，其中a、b、c、d都为实数。当a=0时，q=bi+cj+dk称为纯四元数。近些年，四元数的应用广泛，现利用四元数虚部的相关关系，对粒子群算法进行改进，无论在理论创新和实际应用中，都提供了新思路。

2 算法原理

2.1 基本思想

树状拓扑结构是结合粒子的3个最优值来改变粒子的飞行方向，但无论是个体、局部还是全局的记忆适应值，都忽略了一个问题，就是三者之间的相关性，为了将三者之间的联系用来调节粒子的飞行方向，提出了一种结合四元数理论的改进粒子群算法，利用TPSO作为模型，将个体最优、局部最优和全局最优作为四元数的3个虚部，将四元数作为关联项加入粒子群速度公式的“社会”部分。同时在公式中使用了惯性权重和收缩因子，以保证群体可收敛到全局最优值。

当a=0,b=c=d=1时，将单位纯四元数q=i+j+k代入PSO公式，则改进算法的速度与位置公式为

vi+1,j=χ[wvi,j+c1r1(pi,j-xi,j)+c2r2(pn,j-xi,j)+

c3r3(pg,j-xi,j)+c4r4(qi,j-xi,j)]

(1)

xij(t+1)=xij(t)+vij(t+1)

(2)

式中：x为位置；v为速度；i为当前粒子；j为当前维数；t为当前迭代数；qi,j=pi,j+pn,j+pg,j，pi,j记录粒子个体的最佳解，pn,j记录局部邻域内的粒子最佳解，pg,j记录全局粒子的最佳解；χ为收缩因子；w为惯性权重；c1为调节个体最优的加速系数；c2为调节局部最优的加速系数；c3为调节全局最优的加速系数；c4为调节三者关系的加速系数；r1、r2、r3、r4∈(0,1)且相互独立。

2.2 算法步骤

根据改进算法的设计，下面给出算法的步骤。

步骤1对算法的基本参数进行初始化。

步骤2根据优化函数，计算适应值，并比较记录pi,j、pn,j和pg,j。

步骤3根据步骤2中记录的pi,j、pn,j和pg,j，计算四元数项。

步骤4将四项记录值代入式(1)、式(2)，得到最新迭代次数下的粒子速度和位置。

步骤5根据循环终止条件判断是否满足终止，否则返回步骤2。

在每次迭代中，粒子向全局最优、局部最优及个体最优学习的同时，还保留着三者之间的相关性，此方法使粒子的多样性得到充分利用，避免种群陷入了局部最优而导致无法找到最优解。

2.3 算法收敛性证明

基本微粒群算法中给出了判断PSO收敛性的两个假设条件及全局收敛准则[17-19]。在保证算法有效的前提下，设D为算法迭代方式，用来得到下一次的迭代值，则由D得到的当前迭代值应优于前一次迭代值。因此，提出下列假设以满足算法。

假设1f[D(z,ξ)]≤f(z)，并且如果ξ∈S，S∈Rn，则f[D(z,ξ)]≤f(ξ)。

假设2对于样本空间S的任意Borel子集A，若其测度v(A)>0，则有

(3)

式(3)中：μk(A)为由测度μ(k)所得到的A的概率。

由假设1和假设2给出算法为全局收敛的充要条件。

(4)

式(4)中：P[zk∈Rε]为第k步算法生成的解zk∈Rε的概率。

根据以上假设及定理，证明改进的PSO算法的收敛性。

证明：定义函数D为

(5)

式(5)中：g(xi,k)为改进PSO算法的更新方程。具体为

xi,k+1=g(xi,k)=g1(xi,k)+g2(xi,k)+g3(xi,k)+g4(xi,k)+g5(xi,k)

(6)

式(6)中：g1(xi,k)=xi,k+ωvi,k，g2(xi,k)=c1r1(pi,k-xi,k)，g3(xi,k)=c2r2(pn,k-xi,k)，g4(xi,k)=c3r3(pg,k-xi,k)，g5(xi,k)=c4r4(qi,k-xi,k)，xi,k为第k代时的微粒i的位置，则由定义函数D可知，改进PSO满足假设1。

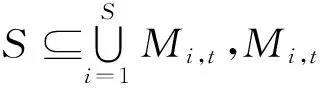
Mi,k=(1+ω-φ1-φ2-φ3-φ4)x(t)-ωx(t-1)+piφ1+pnφ2+pgφ3+qφ4=xi,j,k-1+ω(xi,j,k-1-xi,j,k-2)+φ1(pi-xi,j,k-1)+φ2(pn-xi,j,k-1)+φ3(pg-xi,j,k-1)+

φ4(q-xi,j,k-1)

(7)

3 仿真实验

3.1 测试函数

选择的6个基准测试函数(其中两个单峰值函数，两个多峰值函数及两个多峰固定维度测试函数)如表1所示，对算法进行验证，寻找函数的最小值，并将基本PSO、EDAPSO、TPSO和本文算法对基准函数优化的结果进行比较分析。通过实验的数据来观察在同一测试函数下算法的收敛效率和搜索精度。

3.2 参数设置

根据实验所需参数，对参数的设置如下：最大迭代次数为1 000,惯性权重ω=0.8，收缩因子χ=0.729。粒子规模=30。经实验得到，在本文算法中，c1、c2、c3代表粒子分别向个体最优、局部最优和全局最优学习的随机数，c4代表向三种粒子相关项学习的随机数。当c1=1.4,c2=1.4,c3=1.8,c4=1.4时，取得的效果较好。

3.3 实验结果

3.3.1 仿真实验分析

为了便于考查不同算法的性能，将PSO、EDAPSO、TPSO和本文算法进行比较，将每个算法分别对表1的6个测试函数独立运行30次，记录每种算法在各个函数下的最大值、最小值、平均值及平均时间，具体实验结果如表2所示。对比表2中数据，表明本文算法相对于PSO、EDAPSO和TPSO具有明显的优势。由于在本文算法中加入了四元数为关联的三个记录值，比较表中的数据可以发现，对比最小值结果和函数的最优值，本文算法尤其在F1、F3、F5和F6中可收敛于全局最优值。对于单峰值函数，比较几种算法的平均值可以得出，平均值至少提高10倍，对于F2函数，收敛的平均值有了质的提升，即本文算法在搜索的精度上比其他三种算法高，粒子的多样性得到充分利用。

表1 基准测试函数Table 1 Benchmark function

表2 函数测试结果Table 2 Function test results

对于多峰值函数，在整个函数搜索空间中会包含大量的局部极值，对于PSO算法来说，容易使其陷入局部极值，而本文算法由于利用了TPSO的树状结构，同时加入了四元数项，以使粒子的多样性得到充分利用，使得算法在学习过程中达到了平衡，更容易跳出局部最优值，从而能继续搜索全局最优值。对于多峰固定维测试函数，因其解空间维度较低，不同算法得到的解差异不大，虽然都没有找到真值，但本文算法搜索结果更优。通过几种算法应用于同一约束函数的收敛曲线如图2所示，明显看出本文算法的收敛性优于其他3种算法。

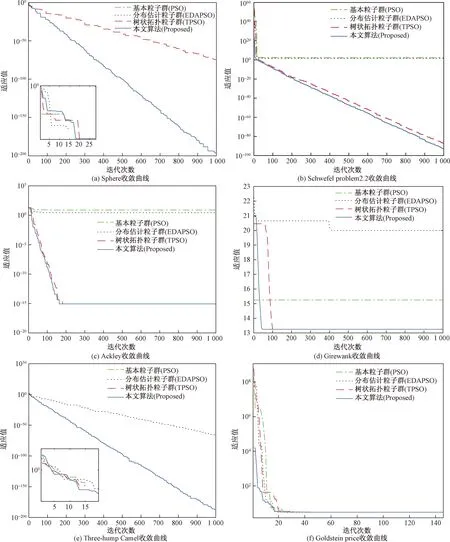
图2 算法的收敛曲线对比Fig.2 Convergence curves comparison of algorithms

3.3.2 物理实验分析

文献[20]中利用粒子群优化算法结合伽马校正，来评估所获得的红外图像增强结果。借鉴此经验，选取图像集中的3幅图像进行对比度增强实验，增强后效果如图3所示：将本文算法与PSO算法进行对比度图像增强算法比较，采用5个图像质量准则进行性能评价，评价结果如表3～表5所示。评价准则包括：峰值信噪比(peak signal to noise ratio, PSNR)；结构相似度指数测度(structural similarity, SSIM)；信息保真度准则(information fidelity criterion, IFC)；视觉信息保真度(visual information fidelity, VIF)；特征相似性(feature similarity, FSIM)。所有这些准则都被广泛应用于图像对比度增强领域，对各种图像对比度增强方法进行性能评价。物理实验中PSO算法的参数设置如下:种群大小为30，最大迭代次数为1 000，c1、c2、c3代表粒子分别向个体最优、局部最优和全局最优学习的随机数，取c1=1.4,c2=1.4,c3=1.8。

图3 测试图像对比Fig.3 Test image comparison

表3 测试图像1对两种方法性能评估Table 3 The performance evaluation of two approaches using test images 1

表4 测试图像2对两种方法性能评估Table 4 The performance evaluation of two approaches using test images 2

4 结论

改进的粒子群算法在TPSO树状结构的基础上，选择局部最优的粒子节点，与个体最优粒子和全局最优粒子之间相关联，通过四元数的数学概念，将这三者设为四元数的三个虚部向量，作为社会部分，加入速度公式中。对改进的算法通过理论证明算法具有全局收敛性，通过仿真实验对算法的收敛性进行可视化说明，改进的PSO算法不但减缓粒子群优化算法的收敛，而且有效地解决了搜索精度不高和容易陷入局部最优值的问题。在算法效率上通过与PSO、EDAPSO和TPSO进行分析比较，具有显著的算法性能，既验证了它的理论可行性，又仿真了算法的实验可行性。对所提算法与其他进化算法优化对比度增强进行比较，选择两个不同数据集中的图像进行主观与客观评价，最后结果得出，无论在主观定性方面还是客观定量方面，本文算法的效果都要优于其他算法。