Yu-Guo Su(苏玉国), Fei Yao(姚飞), Hong-Bin Liang(梁宏宾), Yan-Ming Che(车彦明),

Li-Bin Fu(傅立斌)2, and Xiao-Guang Wang(王晓光)1,†

1Zhejiang Province Key Laboratory of Quantum Technology and Device,Department of Physics,Zhejiang University,Hangzhou 310027,China

2National Laboratory of Science and Technology on Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

Keywords: Majorana’s stellar representation,Bloch sphere,high-dimensional projective Hilbert space,mixedspin

1. Introduction

It is acknowledged that the evolution of an arbitrary twolevel state can be exactly represented by the trajectory of a point on the Bloch sphere.[1-3]Applied to a quantum state in a high-dimensional Hilbert space, this geometric interpretation seems difficult to imagine. Although we can map the quantum pure state to a higher-dimensional geometric structure,this process is no more an intuitive and legible way to comprehend it. Fortunately, the Majorana’s stellar representation(MSR)builds a wide bridge between the high dimensional projective Hilbert space and the two-dimensional Bloch sphere.[4]Employing the MSR,which represents a quantum pure state of spin-J systems in terms of a symmetrized state of 2J spin-1/2 systems, one can generalize this geometric approach to large spin systems or multilevel systems. Majorana’s perspective is that the evolution of a spin-J state can be intuitively described by trajectories of 2J points on the two-dimensional(2D)Bloch sphere,with these 2J points generally coined as Majorana stars(MSs),rather than one point on an intricate high-dimensional geometric structure. Therefore, this representation spontaneously provides an intuitive way to study high spin systems from geometrical perspectives, which has made the MSR a useful tool in many different fields, e.g., classification of entanglement in symmetric quantum states,[5-12]analyzing the spectrum of the Lipkin-Meshkov-Glick model,[13,14]studying Bose condensate with high spins,[15-22]and calculating geometrical phases of large-spin systems.[23-25]In addition,the MSR can be employed in quantum metrology[26,27]and in describing polarization states of N photons.[28]

Moreover, the MSR provides many useful insights into high dimensional quantum states. The Berry phase, which is a unique character of a quantum state[29]and has become a central unifying concept for the quantum state,[30,31]unveils the gauge structure associated with cyclic evolution in Hilbert space.[32]When it comes to an arbitrary two-level state, the Berry phase is simply proportional to the solid angle subtended by the close trajectory of a point on the Bloch sphere,while every star in the MSR will trace out its own trajectory on the Bloch sphere for a cyclic evolution of a large spin state.For example, the Majorana stars can be driven moving periodically on the Bloch sphere and making up the so-called“Majorana spin helix”[21]by the spin-orbit coupling in highspin condensates. Consequently, by asking what the explicit relation between the Berry phase and the Majorana stars’helixes or loops is,it has turned into a significant topic in recent years.[23,24,33-35]

Except for the Berry phase, entanglement is another important unique character of a many-particle quantum state. Although the classification and measure are quite complex[10,36-39]for the multiqubit states, the MSR naturally provides an intuitive way to consider the multiqubit entanglement,[40]since a spin-J state is equivalent to a symmetric 2J-qubit state. The distribution of the Majorana stars not only discloses the relationship between the symmetry of the state and the multiparticle entanglement measures, including geometric measures[9,41-43]and Barycentric measures,[7]but also can be employed to investigate entanglement classes,[44,45]entanglement invariants,[46]and so on.Hence, it is another challenging task to connect the quantum entanglement of the qubits to the distribution of the Majorana stars on the Bloch sphere.

Furthermore, it is interesting to apply this approach to study the multiband topological systems. For a two-band system, e.g., the Su-Schrieffer-Heeger (SSH) model,[47-49]the geometrical meaning of topologically different phases can be revealed by their distinct trajectories,[50,51]with mapping the Bloch state into a 2D Bloch sphere. As a paragon topological model,[52]the SSH model supports either topologically trivial or nontrivial phase, characterized by the quantized Berry phase 0 or π,[29,53,54]which is verified in the recent cold atom experiment.[55]

From Refs. [4,56,57], an arbitrary pure state for spin J can be represented by

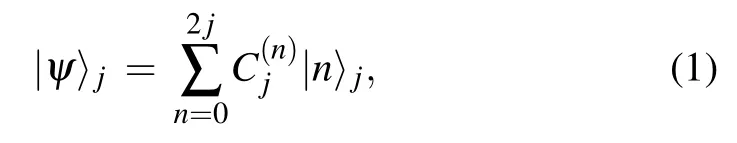
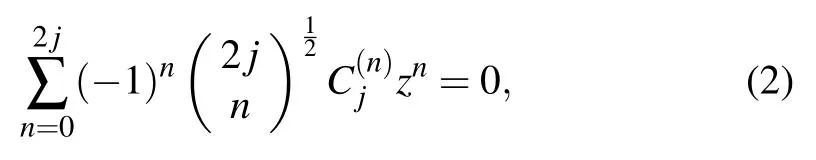
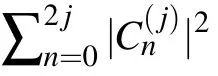
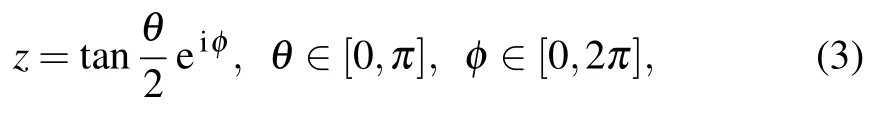
where θ and φ are the spherical coordinates.

The work of Brody and Hughston[58,59]gives an intuitive formalism around higher-dimensional geometries of pure states. They formulated the principles of classical statistical inference in a natural geometric setting and gave a number of examples of features in the state spaces for higher-dimensional systems. The two-spin coupling system(a large spin coupling with a small spin)is significant in many physical fields,such as quantum criticality[60]and quantum dynamics.[61]However,the representation of a two-spin coupling system has been studied fragmentarily,[62-65]which did not generalize to an arbitrary spin-s and was not visible enough. In this work, we choose mixed-spin (s,1/2) systems as paragons to take advantage of the fact that it can be decomposed into two spins:spin-(s+1/2)and spin-(s −1/2). Benefiting from the MSR,we represent an arbitrary pure state on a Bloch sphere. Besides, we propose a practical method to decompose the arbitrary pure state that can be regarded as a state of a pseudo spin-1/2. For the arbitrary pure state of mixed spin, the system can be decomposed into two spins: spin-(s+1/2) and spin-(s −1/2). Consequently, the arbitrary pure state of the mixed spin can be regarded as a state of a pseudo spin-1/2.In this way, the mixed spin decomposes into three spins,and our task is resolving these star equations and obtaining(2s+1)+(2s−1)+1=4s+1 sets of stars.

Our study provides an intuitive perspective of a two-spin(s and 1/2) system and unveils the intrinsic property of the two-spin system on a Bloch sphere, which shall deepen our comprehension of the spin-(s,1/2) system. The paper is organized as follows. In Section 2, we study the fundamental theory of the MSR to describe an arbitrary pure state of spin-(s,1/2),through coupling bases. In Section 3,we give a concise example of the MSR of the mixed-spin (1/2,1/2) systems. In Section 4,we show more applications of our method in the mixed-spin (s,1/2) systems. A brief discussion and summary are given in Section 5.

2. Theory of Majorana representation for mixed-spin(s,1/2)systems

In this section, we will study the fundamental theory of the MSR for the mixed-spin (s,1/2) systems. Firstly, we illustrate with the mixed spin-(1/2,1/2)system to give a legible view of our main logic.Besides,we introduce the coupling bases to present an arbitrarily mixed spin-(s,1/2)state as two independent spins. Finally, benefiting from the new form, a two-level system can be constructed to describe the arbitrary pure state.

For two spin-1/2 particles,an arbitrary pure state can be represented by

We can rewrite Eq.(4)

For a more general case,we can treat the system as a twolevel energy system, which can be represented as two sets of stars on a Bloch sphere if it is a pure state. To normalize the states,we rewrite Eq.(5)as

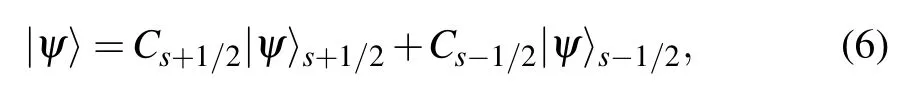
where|ψ〉s+1/2and|ψ〉s−1/2represent the normalized analogous triplet and the normalized analogous singlet. We write the whole initial state as a superposition of two orthogonal states|ψ〉s+1/2and|ψ〉s−1/2. We also have the normalization condition|Cs+1/2|2+|Cs−1/2|2=1,so we only have one independent variable to describe the relation between them,which means that it needs one set of stars on the Bloch sphere to be represented. Based on Eqs.(2)and(6),we can treat the state as a pseudo spin-1/2 and have the star (root) of the pseudo spin

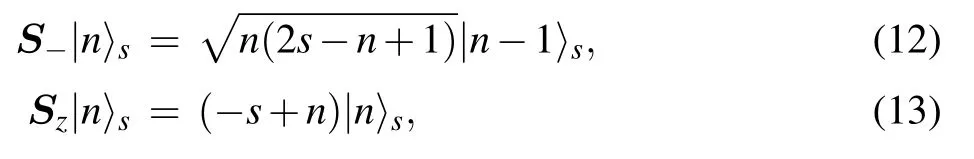
where the angular momentum S = Sx+Sy+Sz, the raising(lowering)operator S+=Sx±iSyand|n〉s≡|−s+n〉sis the basis state. Besides, we write the uncoupling basis state as |n〉s⊗|1〉1/2≡|n〉1|1〉2, |n〉s⊗|0〉1/2≡|n〉1|0〉2, and n=0,1,...,2s.

Then we have the Hamiltonian

From Eqs.(10)-(14),we can rewrite the Hamiltonian as

which reveals the relation between the analogous triplet and the analogous singlet. Because the orthogonality of |ψ〉s+1/2and |ψ〉s−1/2do not constrain the phase difference between them, we choose zero phase difference and keep the star of the pseudo spin on the prime meridian in MSR. Noticing the completeness condition,if one obviates the state only has components in some parts of the whole sectors,one finds that the mapping is injective. Therefore,we need(2s+1)sets of stars to represent the analogous triplet,(2s−1)sets of stars to represent the analogous singlet, and one set of stars to combine the two parts on a Bloch sphere.

From Eqs.(1)and(2),we can get all stars

where the two-dimensional matrix

for n=1,...,2s,A0=A2s+1=(s2+2s+3/4).From Eq.(16),we diagonalize Anand then get the eigenvalue j±(j±+1)(j±=s±1/2)of the An,and the relationship between the coupling and the uncoupling representations

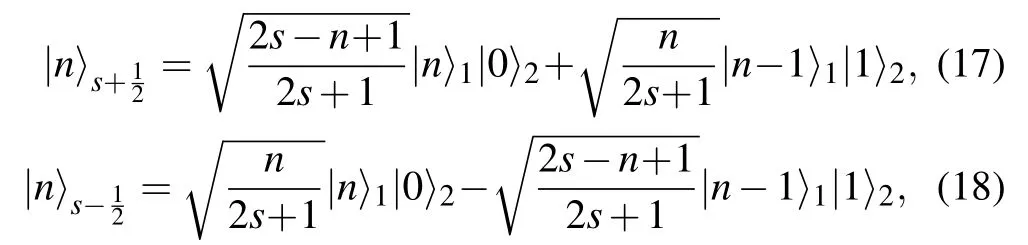
where n=1,...,2s,|n〉s+1/2and|n〉s−1/2denote the coupling basis states.

From Eqs.(17)and(18),we can get the uncoupling basis states

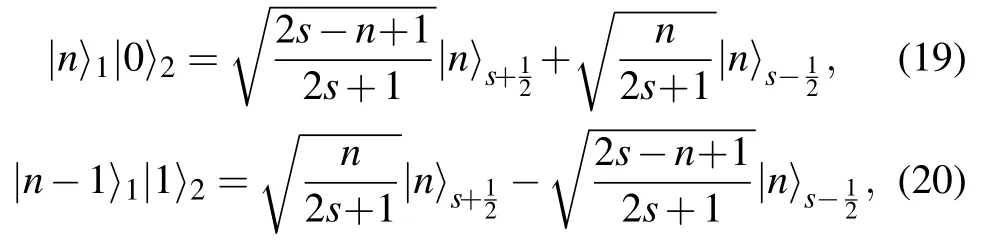
where n=1,...,2s.

For a mixed spin-(s,1/2) system, using Eqs. (19) and(20),we can rewrite the arbitrary state

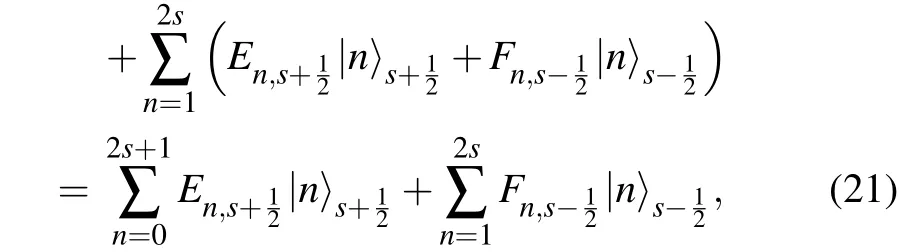
where

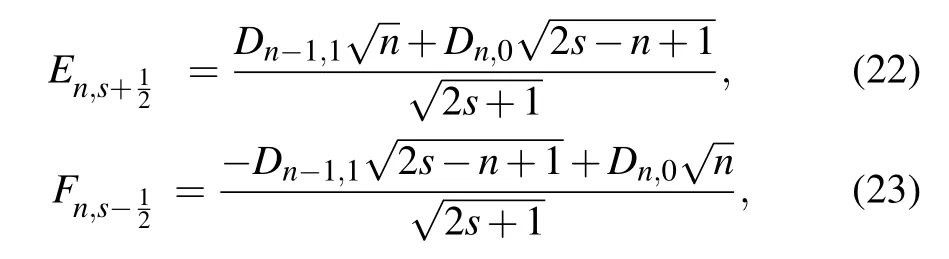
and n = m+1, Dm,1= Dn−1,1, Dn,0are the coefficients of the eigenstates, respectively. We notice that the terms of the bracket are the analogous multiplet and the last term is the analogous singlet.

3. Application in mixed-spin (1/2, 1/2) systems with a real phase parameter ϕ and time evolution

In this section, we will show a concise example for the mixed-spin(s,1/2)systems with a real phase parameter ϕ.

From Eqs.(3),(8)and(9),we use two sets of stars to represent the analogous triplet,no star to represent the analogous singlet and one set of stars to combine the two parts on a Bloch sphere.

To illustrate the idea above, we give a simple spin-(1/2,1/2)system with time evolution:

where the Hamiltonian H1=σ1xσ2x+σ1yσ2y+δσ1zσ2z,δ ∈[0,1] and the real phase parameter ϕ ∈(0,π/2)∪(π/2,π)∪(π,3π/2)∪(3π/2,2π), considering the completeness condition.

Therefore,we gain triplet stars

However,the singlet state has no star. The stars(roots)of the pseudo spin

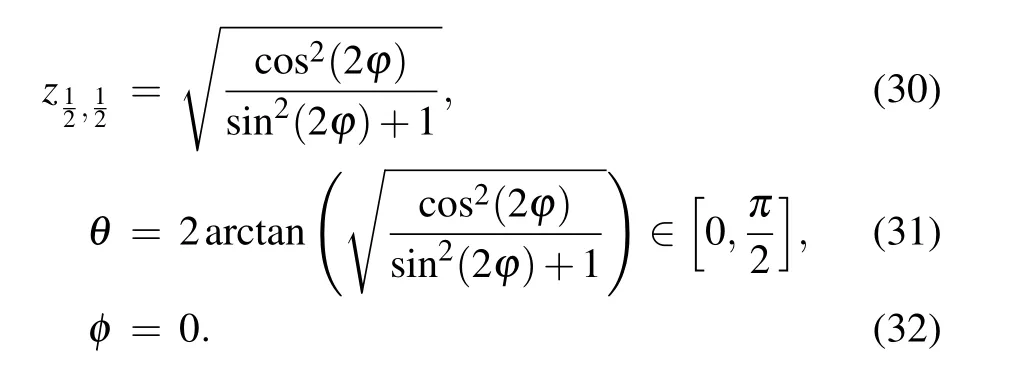
Hence, we know that the stars of the pseudo spin are always mapped to the north of the prime meridian and they are independent of time evolution. To show the idea above, we give a brief example of the two spin-1/2 particles with the real phase parameter ϕ,time evolution and δ =0.

Figure 1 shows the stars of the two spin-1/2 particles represented in the Bloch sphere with real phase parameter ϕ,time evolution and δ=0.Without time evolution,because the roots(z1)in our example are always real,with the variety of the real phase parameter ϕ, each set of the triplet stars is mapped to the north or south prime meridian. Intuitively,the stars of the pseudo spin only cover the north prime meridian. Since star equation of the analogous singlet does not have root in two spin-1/2 case,we do not have singlet state star(Fig.1(a)).Our method applies two, zero and one sets of stars to present the spin-(1/2+1/2), the spin-(1/2 −1/2) and the pseudo spin-1/2,respectively.Obviously,the position of the star of pseudo spin unveils the relationship of corresponding coefficients between |ψ〉s+1/2and |ψ〉s−1/2. For example, if the latitude of the star of pseudo spin rises and the stars of pseudo spin are sparse,it means that the proportion of|ψ〉s−1/2increases and the speed of the change is high. Fixed the time at a special value,we can distinctly find that one set of the triplet stars and the others are 180◦rotational symmetric around the x-axis(the intersecting line of the prime meridian plane and the equatorial plane) (Fig.1(b)). As seen in Fig.1(c), the triplet stars are mapped to the prime meridian at t=2kπ/4,the 90◦W(E)meridian at t =(2k+1)π/4 (k is integer). Fixed the phase parameter ϕ at a special value, since stars of the pseudo spin are independent of time evolution,they are fixed at particular positions (Fig.1(d)). Meanwhile, each set of the triplet stars is plane symmetry around the equatorial plane and the prime meridian plane at a whole period T = π, and each set still keeps the rotational symmetry at every single time and phase parameter value.

The method we proposed can visualize the mixed-spin(s,1/2)system and describe the entanglement of the system. For the mixed-spin(1/2,1/2)system,the distributions of specific states’ stars in Majorana’s stellar representation are given in Table 1.

Fig.1. Bloch representation of the two spin-1/2 particles with the real phase parameter ϕ,time evolution and δ =0. (a)-(c)The stars are mapped to the Bloch sphere with the variety of ϕ,meanwhile,without time evolution. (a)All stars with t =0. (b)All stars with t =π/6 and ϕ =π/3. (c)The triplet stars with t=π/4. (d)All stars are mapped to the Bloch sphere with the period of time evolution T =π and ϕ =2π/3. The red circles and red dots represent the stars of the triplet;purple crosses represent the stars of the pseudo spin.

Table 1. Specific states’stars of mixed-spin(1/2,1/2)systems in Majorana’s stellar representation.

4. Application in mixed-spin (s, 1/2) systems with a real phase parameter ϕ and time evolution

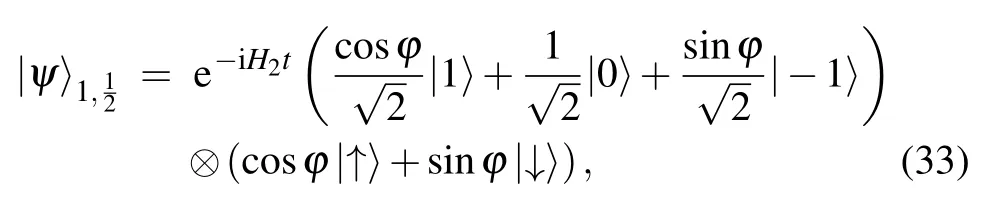
In this section, we will give brief examples with a real phase parameter ϕ, time fixed case, and with time evolution,fixed real phase parameter ϕ case for the mixed-spin(s,1/2)systems,respectively. To illustrate the idea above,let us consider the example spin-1 and spin-1/2 case as where the Hamiltonian H2=S1xS2x+S1yS2y+δS1zS2z,S1i(respectively,S2i,i=x,y,z)are the three direction components of the larger spin(respectively,spin-1/2),|1〉,|0〉,|−1〉are the eigenstates of the spin-1 particle, and |↑〉, |↓〉 are the eigenstates of the spin-1/2 particle. So we have unitary transformation operator U =exp(−iH2t).

Utilizing Eqs.(1)and(21),we have

From Eq.(2),we obtain

where zj,z1,1/2denote the characteristic variables of the spin-j case and the pseudo spin case,respectively,and we also have the normalization condition|C1+1/2|2+|C1−1/2|2=1.

Solving Eqs.(35)and(36),we can easily gain the whole bloch representation of the spin-s and spin-1/2 particles system with Eq. (3). To illustrate the idea above, we show the bloch representation of the spin-s and spin-1/2 particles system with time evolution,the real phase parameter ϕ and δ =0.

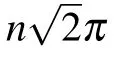
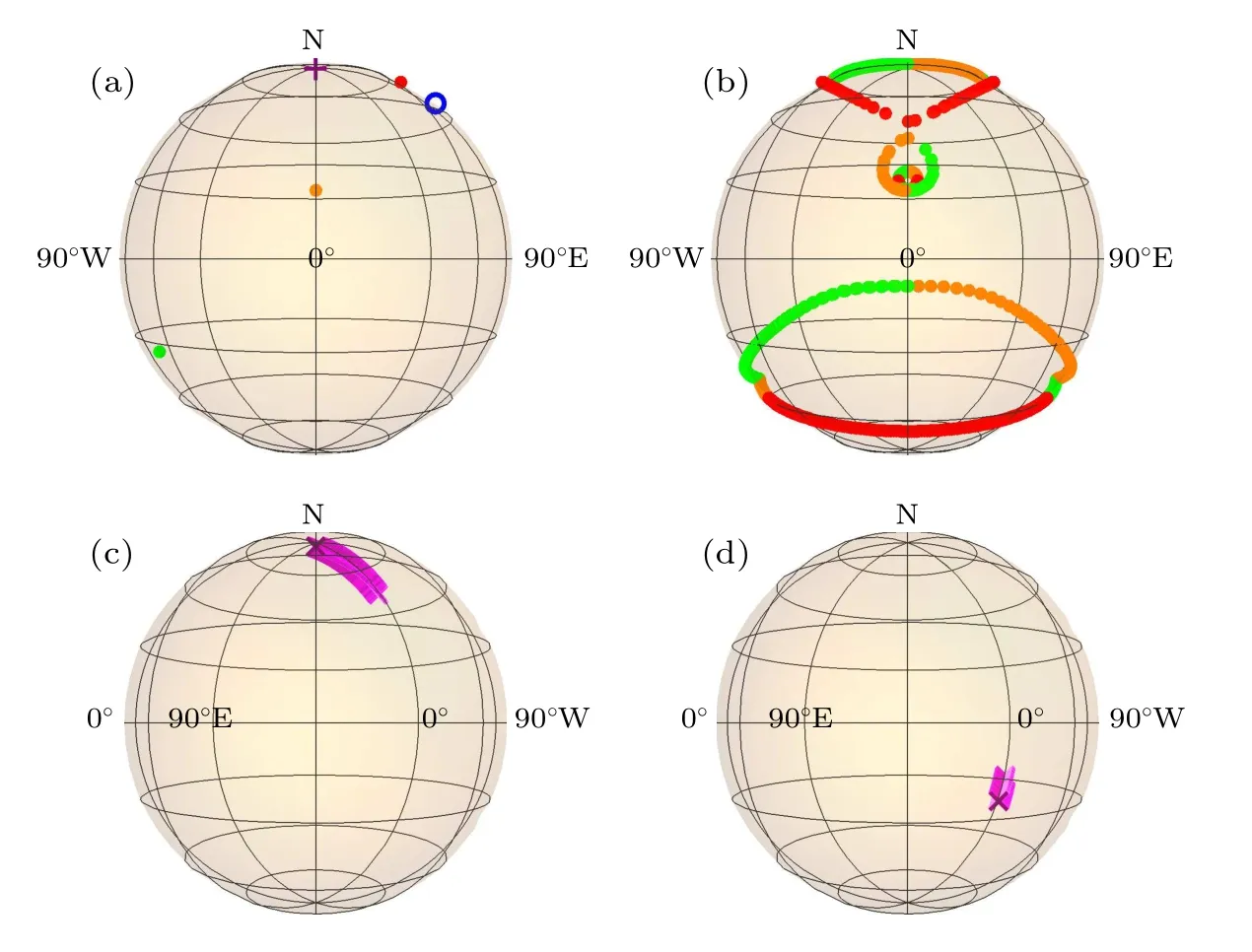
Fig.2. Bloch representation of the spin-1 and spin-1/2 particles system with time evolution t ∈[0,4π],fixed real phase parameter ϕ and δ =0. (a)All stars with ϕ =π/6 when time fixed at t=1π/4. (b)The analogous multiplet stars with the phase parameter fixed at ϕ =π/6. (c)and(d)The stars of the pseudo spin at ϕ =π/4 and ϕ =5π/4. The red dots, green dots and orange dots represent the stars of the analogous multiplet, blue circles represent the stars of the analogous singlet,and purple plusses represent the stars of the pseudo spin.

Fig.3. Bloch representation of the spin-1 and spin-1/2 particles system with the real phase parameter ϕ variety, fixed time and δ =0. (a) All stars with ϕ =3π/4 and t =π/2. (b)-(d) Two sets of the analogous multiplet stars, another set of the analogous multiplet stars and the stars of the pseudo spin are mapped to the Bloch sphere with the variety of ϕ and time fixed at t =0, respectively. (e)The stars of the pseudo spin with t=π/√. (f)The analogous multiplet stars with t=π/3. The red dots,green dots and orange dots represent the stars of the analogous multiplet,blue circles represent the stars of the analogous singlet,and purple plusses represent the stars of the pseudo spin.

5. Conclusion

Recently, the Majorana’s stellar representation and relevant applications have demonstrated that the distributions and motions of the Majorana stars on the Bloch sphere have become a new and effective tool to study the symmetry-related questions in the high-dimensional or many-body system. Our study here shows that, utilizing the MSR, an arbitrary pure state can always be represented on a Bloch sphere with 4s+1 stars in a two-spin (s and 1/2) system. We take the system described by coupling bases as a state of a pseudo spin-1/2.Furthermore,we propose a practical method to decompose the arbitrary pure state that can be regarded as a state of a pseudo spin-1/2.

As we know, a star on a Bloch sphere can represent a pure state, and a set of stars on a Bloch sphere can represent high-dimensional pure states. However, this method cannot be applied in arbitrary high-dimensional mixed states. Our result is not easy to be generalized to arbitrary high-dimensional mixed-spin systems, such as a mixed-spin (s,1) system. We cannot directly use an effective pseudo spin 1 to describe it.

Taking advantage of the MSR, which provides an intuitive way to study high spin system from a geometrical perspective, we can have a novel and holonomic view to investigate the intricate system. Considering spin-(1/2,1/2) and spin-(1,1/2)systems, we find that one can easily distinguish between non-entangled states and entangled states by the distribution of stars in MSR. Since we have presented a general method to visualize the mixed-spin(s,1/2)systems, one can further apply the method in many situations,such as quantum transitions and quantum tunneling in quantum spin baths and quantum dots.

Acknowledgment

We thank Jing Cheng for the useful discussions.