张杰华,周实然

(1.凯里学院理学院,贵州 凯里 556011)

(2.凯里学院教育科学学院,贵州 凯里 556011)

1 引言

随着微分方程理论的不断发展,两点边值问题的研究也日益活跃,它在工程力学、天文学、经济学、控制论及生命科学等领域的许多实际问题中都有着广泛的应用.有限体积法,又被称之为广义差分法、控制体积法,它兼顾了有限差分法和有限元法各自的优点,是求解偏微分方程的一种有效数值方法[1].

众所周知,有限元法及其超收敛理论研究已经比较完善[2,3],而有限体积法的研究还不尽人意.关于求解两点边值问题的有限体积法研究,多年来硕果累累.上世纪八、九年代,学者们已经开始致力于有限体积法的基础理论研究[4–7].到了本世纪初,关于高阶有限体积法及其超收敛理论分析的研究,开始逐渐成为关注的热点,进入学者们的视野[8–15].特别地,文献[16]证明了线性有限体积法的解与相应的有限元法的解具有H1模超逼近性质.专著[17]给出了两点边值问题二阶与三阶有限体积法的H1模超逼近及其应力佳点的超收敛结论.文献[18]建立了基于应力佳点的三阶有限体积法并得到了关于其导数误差估计的超收敛结果.文献[19–21]给出了两点边值问题的任意阶有限体积法在节点处与高斯点处的超收敛分析.虽然,大部分的这些研究工作分析了对应的有限体积法的最优H1模和L2模误差估计,给出了应力佳点处的导数误差估计以及整体的H1模超收敛结果,但都很少提及有限体积法的L2模超逼近和超收敛后处理估计.

此外,近年来基于三角形网格剖分的有限体积法研究也取得了突破性的进展.文献[22,23]借助于离散范数等价,在三角形网格上分析了一类椭圆问题的高阶有限体积法的强制性要求.文献[24]通过选取特殊的三角形对偶剖分,利用从试验函数空间到检验函数空间的特殊映射,构建了与三角形形状无关的无条件稳定的二阶有限体积法.正是这些已有的研究成果启发了本文的工作.

本文基于Lagrange二次有限体积法,构造求解两点边值问题的一种新Lagrange二次数值方法,得到了新方法的H1模和L2模的超逼近估计.具体地,基于有限体积法[24]构造特殊对偶剖分及其特殊映射的思想,引入从Lagrange二次有限体积法的试验函数空间到检验函数空间的一个新映射,从而得到求解两点边值问题的一种Lagrange二次新数值方法.此数值方法在特殊对偶剖分时即为Lagrange二次有限体积法.借助于文献[22,23]中离散等价范数的技巧,利用等价二次型的性质,本文构造了与H1模,H2离散半模等价的离散范数,证明了对任意的Lagrange二次对偶剖分此文的数值方法均具有最优H1模误差估计.特别地,当对偶剖分单元节点取为应力佳点(Gauss点)时,本文分析了新数值方法的第一型和第二型插值弱估计,从而得到了H1模和L2模的超逼近估计(第二型插值弱估计是得到L2模超逼近的关键).对此特殊对偶剖分的数值解作局部二级插值处理,则可得到新数值方法的整体H1模和L2模超收敛估计,其收敛阶与其对应的二次Lagrange有限元法结论一致.利用本文的技巧,同样可分析Lagrange二次有限体积法的超收敛结论.另外,本文的思想与方法可以扩展至高维高阶的数值方法情形.

下一节,本文将给出求解两点边值问题的Lagrange二次新数值方法.第三节将给出离散范数等价估计.第四节考虑对任意二次对偶剖分新数值方法的最优H1模误差估计.第五节,采用特殊对偶剖分,分析新数值方法的第一型及第二型插值弱估计,并证明数值解的H1模和L2模超逼近估计,以及利用二级插值处理后的超收敛估计.最后,给出数值算例,说明本文理论结果的正确性.

2 新Lagrange二次数值方法

方程(2.6)即为本文所分析的求解两点边值问题的Lagrange二次新数值方法.

3 等价范数

4 H1误差分析

book=180,ebook=89

5 超收敛估计

6 算例

本节给出数值算例,验证数值方法(2.6)的有效性及其超逼近,超收敛估计.本文中的所有数值计算均是在个人PC机上利用Matlab(R2010b)软件计算得到.采用GMRES迭代方法求解线性方程组(2.6),取其截断误差为10−10.表格中的,h为单元长度.

考虑如下两个两点边值问题.

例 6.1设方程(2.1)中的p(x)=1,a=0,b=1,其真解为u=exsin(πx)+πex−π,x∈(0,1).显然有u(0)=u0(1)=0.

例 6.2设方程 (2.1)中的p(x)=e−πx,a=0,b=1,其真解为u=eπxsin(πx)+πeπx,x∈(0,1).显然也有u(0)=u0(1)=0.

表1和表2列出了数值方法(2.6)关于例6.1的计算结果.其中,取参数.从表1的数值结果不难发现,数值方法(2.6)具有最优阶H1模误差估计和H1模,L2模超逼近估计.而表2的数值结果显示,数值方法(2.6)的解经过二级插值处理之后具有H1模,L2模超收敛结果.这些数值结果与本文的理论结果相一致,且与相对应的有限元法具有相同的收敛阶.

表1 数值方法(2.6),例6.1,

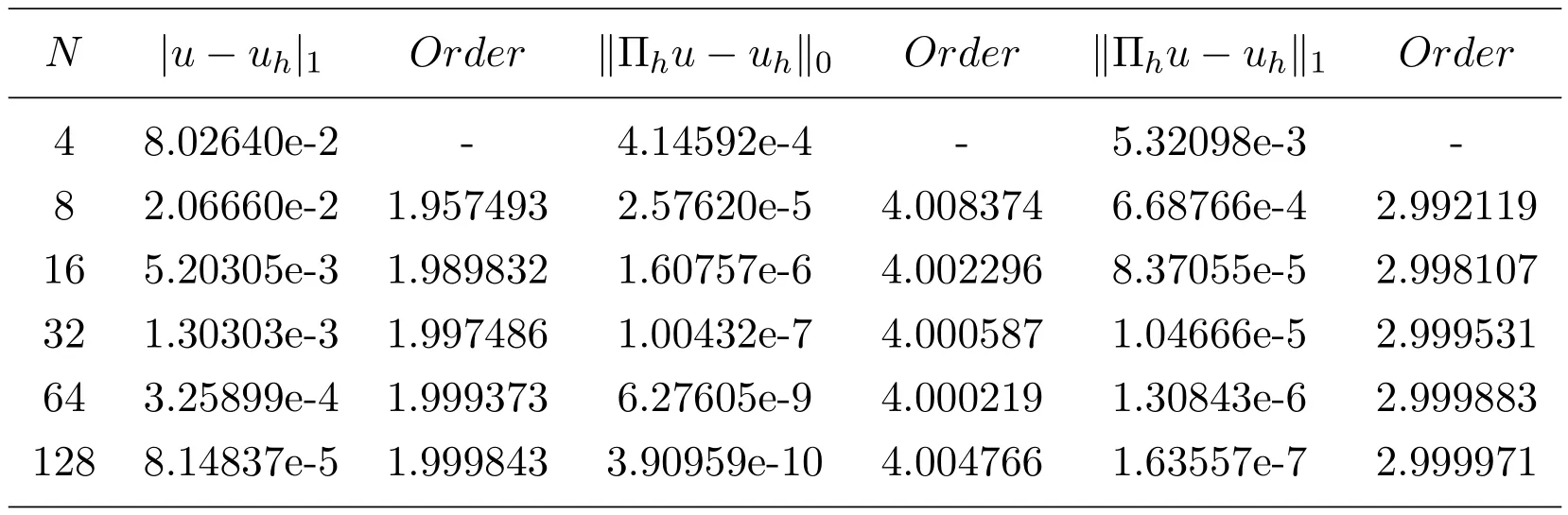
表1 数值方法(2.6),例6.1,

N |u−uh|1 Order kΠhu−uhk0 Order kΠhu−uhk1 Order 4 8.02640e-2 - 4.14592e-4 - 5.32098e-3 -8 2.06660e-2 1.957493 2.57620e-5 4.008374 6.68766e-4 2.992119 16 5.20305e-3 1.989832 1.60757e-6 4.002296 8.37055e-5 2.998107 32 1.30303e-3 1.997486 1.00432e-7 4.000587 1.04666e-5 2.999531 64 3.25899e-4 1.999373 6.27605e-9 4.000219 1.30843e-6 2.999883 128 8.14837e-5 1.999843 3.90959e-10 4.004766 1.63557e-7 2.999971

表2 数值方法(2.6),例6.1,

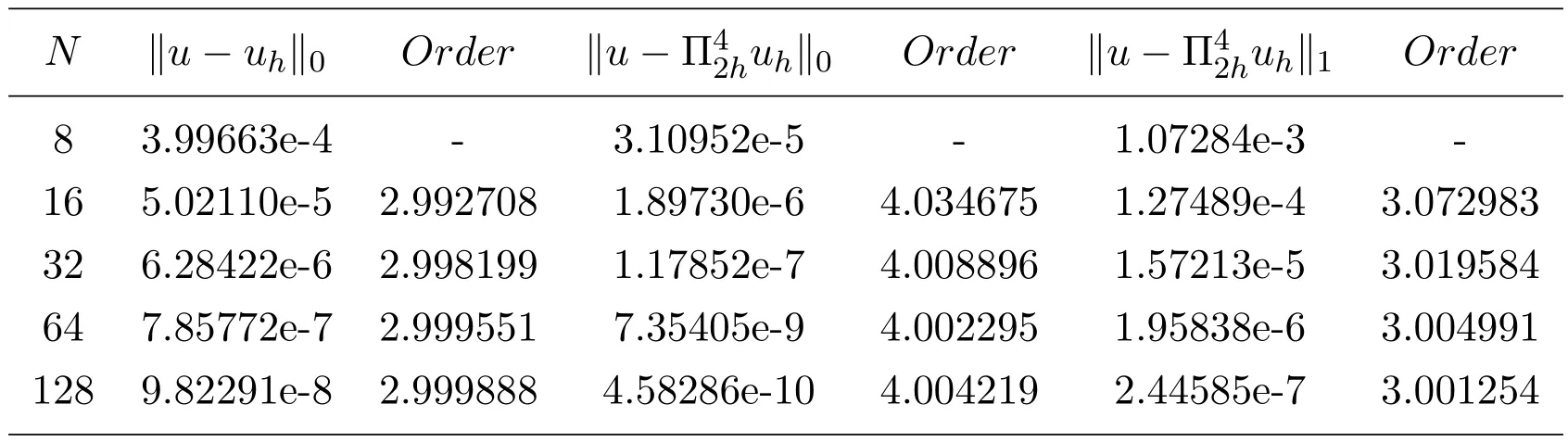
表2 数值方法(2.6),例6.1,

N ku−uhk0 Order ku−Π42huhk0 Order ku−Π42huhk1 Order 8 3.99663e-4 - 3.10952e-5 - 1.07284e-3 -16 5.02110e-5 2.992708 1.89730e-6 4.034675 1.27489e-4 3.072983 32 6.28422e-6 2.998199 1.17852e-7 4.008896 1.57213e-5 3.019584 64 7.85772e-7 2.999551 7.35405e-9 4.002295 1.95838e-6 3.004991 128 9.82291e-8 2.999888 4.58286e-10 4.004219 2.44585e-7 3.001254

表3列出了数值方法(2.6)关于例6.2的最优阶H1模误差估计和H1模,L2模的超逼近估计.表4列出了数值方法(2.6)关于例6.2的H1模,L2模的整体超收敛结果.其中参数仍取.其数据结果再次表明,本文采用的数值方法(2.6)对变系数p(x)的两点边值问题是有效的,且具有最优阶H1模误差估计,H1模和L2模的超逼近及超收敛结果.

表3 数值方法(2.6),例6.2,

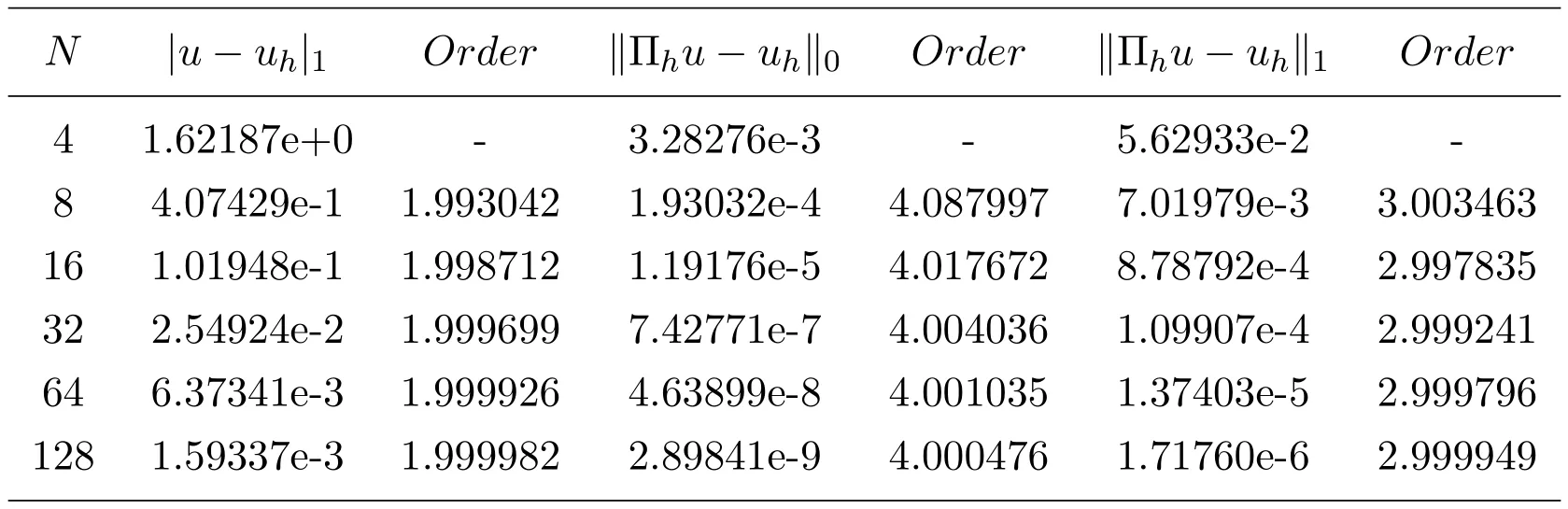
表3 数值方法(2.6),例6.2,

N |u−uh|1 Order kΠhu−uhk0 Order kΠhu−uhk1 Order 4 1.62187e+0 - 3.28276e-3 - 5.62933e-2 -8 4.07429e-1 1.993042 1.93032e-4 4.087997 7.01979e-3 3.003463 16 1.01948e-1 1.998712 1.19176e-5 4.017672 8.78792e-4 2.997835 32 2.54924e-2 1.999699 7.42771e-7 4.004036 1.09907e-4 2.999241 64 6.37341e-3 1.999926 4.63899e-8 4.001035 1.37403e-5 2.999796 128 1.59337e-3 1.999982 2.89841e-9 4.000476 1.71760e-6 2.999949

表4 数值方法(2.6),例6.2,

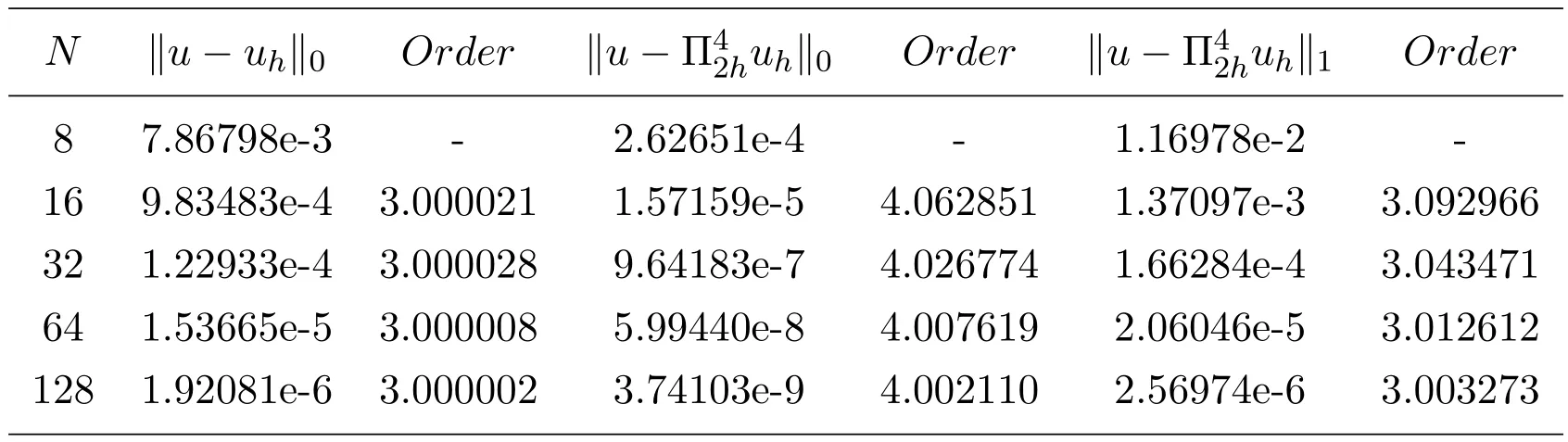
表4 数值方法(2.6),例6.2,

N ku−uhk0 Order ku−Π42huhk0 Order ku−Π42huhk1 Order 8 7.86798e-3 - 2.62651e-4 - 1.16978e-2 -16 9.83483e-4 3.000021 1.57159e-5 4.062851 1.37097e-3 3.092966 32 1.22933e-4 3.000028 9.64183e-7 4.026774 1.66284e-4 3.043471 64 1.53665e-5 3.000008 5.99440e-8 4.007619 2.06046e-5 3.012612 128 1.92081e-6 3.000002 3.74103e-9 4.002110 2.56974e-6 3.003273

表5 数值方法(2.6),例6.2,

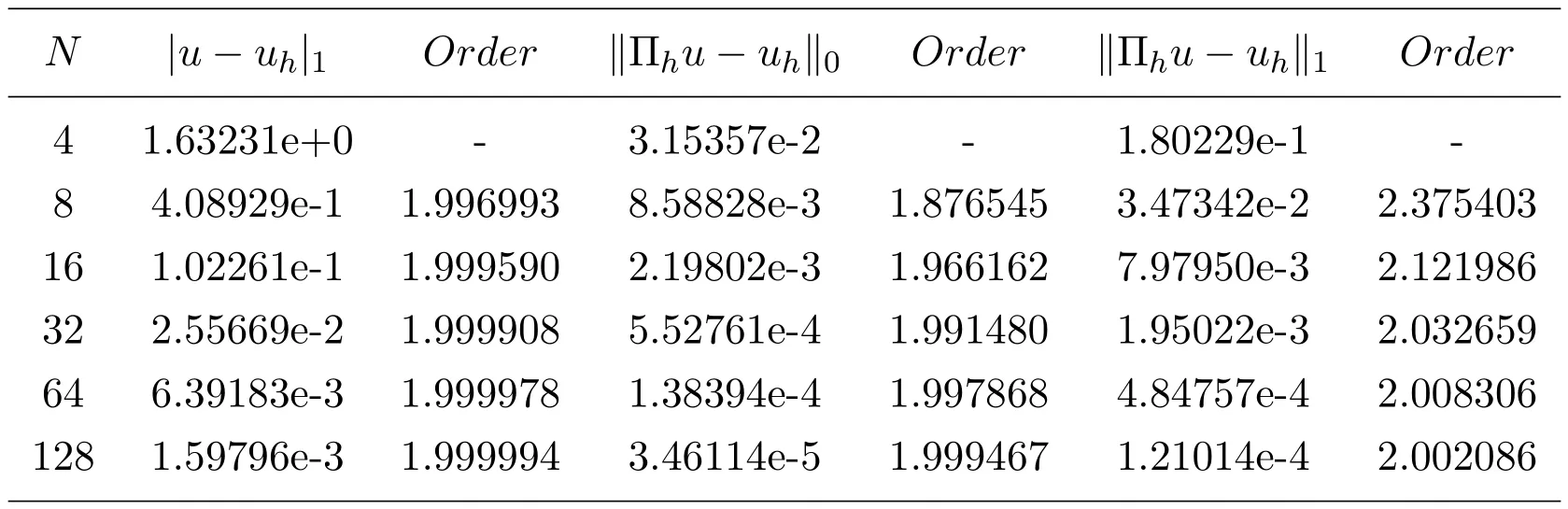
表5 数值方法(2.6),例6.2,

N |u−uh|1 Order kΠhu−uhk0 Order kΠhu−uhk1 Order 4 1.63231e+0 - 3.15357e-2 - 1.80229e-1 -8 4.08929e-1 1.996993 8.58828e-3 1.876545 3.47342e-2 2.375403 16 1.02261e-1 1.999590 2.19802e-3 1.966162 7.97950e-3 2.121986 32 2.55669e-2 1.999908 5.52761e-4 1.991480 1.95022e-3 2.032659 64 6.39183e-3 1.999978 1.38394e-4 1.997868 4.84757e-4 2.008306 128 1.59796e-3 1.999994 3.46114e-5 1.999467 1.21014e-4 2.002086

7 结论

本文构造了求解两点边值问题的一种新Lagrange二次数值方法,利用等价离散范数证明了该方法的第一型与第二型弱估计,从而得到该数值方法的整体H1模和L2模超逼近结果,其收敛阶与对应的有限元法结果相一致.本文的思想与方法可以扩展至高维高阶的有限体积法情形.