WANG Pengjun, WANG Lijin

(School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China)

Abstract We propose a class of stochastic Poisson integrators based on Padé approximations for linear stochastic Poisson systems. The root mean-square convergence orders of the schemes are analyzed, and the structure preserving properties are investigated. Numerical tests are performed to verify the theoretical results and illustrate the numerical behavior of the proposed methods.

Keywords stochastic Poisson integrators; root mean-square convergence order; Padé approximations; Poisson structure; Casimir functions

Stochastic Poisson systems are defined as stochastic systems of the form[1]

X(t0)=x,

(1)

whereX(t),x∈Rn,B(X)=(bij(X))∈Rn×nis a skew-symmetric matrix-valued function satisfying

(2)

for alli,j,k. It is called the structural matrix.Hi(i=0,…,s) are smooth scalar functions, and (W1(t),…,Ws(t)) is ans-dimensional standard Wiener process. The small circle “∘” before dWidenotes stochastic differential equations of Stratonovich sense.

It can be proved that[1], almost surely, the phase flowφt:x|→X(t) of the stochastic Poisson systems (1) preserves the Poisson structure

(3)

As was given in Refs.[1,5-7], etc., a functionC(X) is called a Casimir function of a Poisson system with structural matrixB(X), if

(4)

It is not difficult to prove that (see Ref.[1]), the Casimir functionsC(X) are invariants of the stochastic Poisson systems (1).

Numerical methods preserve the Poisson structure and the Casimir functions, namely, the methods {Xn} satisfying

C(Xn+1)=C(Xn), ∀n≥0,

(5)

are called Poisson integrators[6]. Poisson integrators for deterministic Poisson systems have been developed from various points of view (see Refs.[5-7] and references therein). Numerical methods for stochastic Poisson systems, however, are still rarely studied, except in a number of recent papers on structure-preserving methods for certain special stochastic Poisson systems with single noise or/and even dimensions (e.g., Refs.[8-9]), as well as our paper (Ref.[1]) on numerical methods based on Darboux-Lie theorem for general stochastic Poisson systems.

In this paper, we consider linear stochastic Poisson systems of the form

(6)

(7)

where

Ai=BCi,i=0,…,s.

The exact solution of (7) is of the form

X(t)=

(8)

On the analogy of the discussions for linear Hamiltonian systems in Refs. [5, 10-11], we need to simulate the random matrix exponential in (8) appropriately to obtain high order structure-preserving numerical solvers.

In this paper, we apply Padé approximations to the random matrix exponential in (8), to produce stochastic Poisson integrators which preserve both the Poisson structure and the Casimir functions of the original linear stochastic Poisson systems (7) and possess high root mean-square accuracy. This is an extension of the above-mentioned Padé approximation approaches for linear Hamiltonian systems[5,10-11]to linear stochastic Poisson context.

The contents of this paper are organized as follows. In section 1, we construct the numerical schemes based on the Padé approximations, namely, the (l,m)-schemes. In section 2 we analyze the root mean-square convergence orders of the proposed (l,m)-schemes. In section 3 we prove the preservation of the Poisson structure and the Casimir functions by the (p,p)-schemes, that is, the (l,m)-schemes whenl=m=p. Numerical experiments are performed in section 4 to verify the theoretical analysis and illustrate the numerical behavior of the proposed schemes. Section 5 is a brief conclusion.

1 Numerical schemes based on the Padé approximations

To simulate the random matrix exponential in (8), we can use the following Padé approximation (see e.g. Refs.[10,12])

(9)

whereMrepresents ann×ndimensional square matrix,l,mare positive integers, and

with

|exp(M)-Pl,m(M)|=O(|M|l+m+1).

(10)

Now we construct the following numerical discretization for the linear stochastic Poisson system (7)

(11)

where

tn=t0+nh.

(12)

After the truncation (12), we rewrite the scheme (11) in the following form

(13)

where

(14)

(15)

2 Root mean-square convergence orders

≤K(1+|x|2)1/2hp1,

≤K(1+|x|2)1/2hp2.

(16)

Also, let

(17)

Then for anyNandk=0,1,…,Nthe following inequality holds:

≤K(1+E|X0|2)1/2hp2-1/2,

(18)

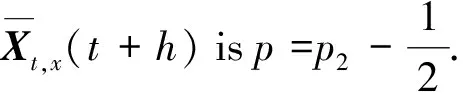
(19)

Using the above fundamental convergence theorem and its corollary, namely the Propositions 2.1 and 2.2, we can prove the following convergence theorem for the scheme (13).

ProofConsider the following scheme:

(20)

which is based on the one-step approximation

(21)

(22)

Then we can derive

(23)

where

Due to the fact that, for square matricesMi(i=0,…,s), and anyj≥1 (j∈Z),

whereρi≥0,ρi∈Z (i=1,…,s).

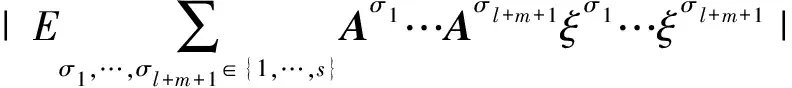
(24)

where

and the last inequality is due to

forν=ρ-uwhich satisfies 1≤ν≤ρ.

(25)

fori=1,…,s. Note thatK1,K2are positive constants independent ofh.

On the other hand,

|E[(ξ1)ρ1(ξ2)ρ2…(ξs-1)ρs-1(ξs)ρs-

≤|E[(ξ1)ρ1(ξ2)ρ2…(ξs-1)ρs-1(ξs)ρs-

…+

|E[(ξ2)ρ2…(ξs-1)ρs-1(ξs)ρs]|+

…+

(26)

From (25) we know that

which, together with (26), implies that

(27)

(28)

Now we estimate the second moment of the error. Applying the inequality

(29)

we have

≤3|x|2(L4+L5+L6),

(30)

where

Meanwhile, it is easy to see thatL5≤O(hl+m+1), the principal term of which, denoted byP5, satisfies

Aσ1…Aσl+m+1ξσ1…ξσl+m+1|2

=O(hl+m+1),

whereK3is a positive constant independent ofh. ThusL5≤O(hl+m+1), and obviously,L6≤O(hl+m+2).

Similar to the analysis for (25), lett=x-Ah, we have for anyρ≥1 (ρ∈Z) that

≤2ρK5h1-ρ+l+m,

(31)

fori=1,…,s, whereK4,K5are positive constants independent ofh.

ForL4, we have

≤E|(ξ1)ρ1(ξ2)ρ2…(ξs-1)ρs-1(ξs)ρs-

…+

E|(ξ2)ρ2…(ξs-1)ρs-1(ξs)ρs|2+

…+

(32)

From (31) we know that fori∈{1,…,s},

which, together with (32), implies that

L4≤O(hl+m+1).

(33)

Considering also the orders ofL5andL6discussed above, we obtain

(34)

whereLis a positive constant independent ofh.

Next we consider the difference:

(35)

where

(36)

(37)

and

=O(hl+m+1),

(38)

□

3 Preservation of the Poisson structure and the Casimir functions

Proposition3.1For anyn≥0,n∈Z,

Proposition3.2Supposef(x) is an even polynomial andg(x) is an odd polynomial, then we have

Now we prove the following theorem:

Theorem3.1The (p,p)-schemes (13) (l=m=p) preserve the Poisson structure of the original linear stochastic Poisson system (7).

ProofRegarding the equivalent form (11) of (13), we need to verify

=B,

(39)

which is equivalent to

(40)

Let

wheref(x) is an even polynomial andg(x) is an odd polynomial. Then it follows

□

Next we prove the Casimir-preservation by the (p,p)-scheme (13).

Theorem3.2The (p,p)-schemes (13) (l=m=p) preserve the Casimir functions of the linear stochastic Poisson system (7).

ProofFrom (13) we know

where

=0,

□

4 Numerical experiments

In this section, we illustrate the performance of the (p,p)-schemes (13) (l=m=p) via numerical tests. We consider the following linear stochastic Poisson system

dX(t)=

X(t0)=x.

(41)

It can be proved that, the functionC(X)=3X(1)+X(2)+X(3)is a Casimir function of the system (41). Moreover, the Hamiltonian functions

H1(X)=(X(1)+X(2))2+(X(1)+X(3))2,

H2(X)=11(X(1))2+2(X(2))2+2(X(3))2+

8X(1)X(2)+2X(2)X(3)+8X(3)X(1)

The stochastic poisson integrators, i.e., the (p,p)-schemes (13) (p=1,2,3) for (41) read

(42)

(43)

(44)

where

Figure 1 illustrates the root mean-square orders of the (p,p)-schemes (42), (43) and (44), which are 1, 2 and 3, respectively, coinciding with the theoretical result in Theorem 2.1. Here we takeT=10, initial valuex=[1,0,-1], and time stepsh=[0.005,0.01,0.02,0.025,0.05]. The expectation is approximated by taking average over 1 000 sample paths.

Fig.1 Root mean-square convergence ordersof (42), (43), and (44)

Figure 2 compares the numerical sample paths ofX(1)(t),X(2)(t) andX(3)(t) arising from the (1,1)-scheme (42) and the implicit Euler method with the reference solution. As can be seen, as time steph=0.01, both numerical methods can create good path approximations. Ash=0.1, however, the implicit Euler fails to simulate the paths in acceptable accuracy, while our (1,1)-scheme (42) still behaves fairly well.

Fig.2 Sample paths produced by (42) and the implicitEuler method for h=0.1 (a) and h=0.01(b)

Fig.3 Preservation of Casimir function by (42),(43), (44)，and the implicit Euler method

Figure 4 observes the evolution of the HamiltoniansH1(X(t)) andH2(X(t)) over the time intervalt∈[0,10], produced by the (1,1)-scheme (42) and the implicit Euler with initialx=[1,1,1], by the (2,2)-scheme (43) with initialx=[1,1,2] and by the (3,3)-scheme (44) with initialx=[1,1,3]. It is clear that, the implicit Euler can not preserve the Hamiltonians, while our (p,p)-schemes (p=1,2,3) can. Here we takeh=0.1.

Fig.4 Evolutions of H1 (a) and H2 (b) by (42), (43), (44), and the implicit Euler method

Fig.5 Error evolutions of the Poisson structure by(42), (43), (44), and the implicit Euler method

5 Conclusion

Theoretical and empirical analyses show that the (p,p)-schemes, based on the Padé approximations, can simulate the linear stochastic Poisson systems with arbitrarily high root mean-square ordersp(p≥1,p∈Z), and preservation of both the Poisson structure and the Casimir functions. They constitute a class of stochastic Poisson integrators for linear stochastic Poisson systems, whose superiorities to non-Poisson integrators are illustrated by numerical experiments.