贾鸣明，陈含爽，张海峰

（安徽大学1.数学科学学院，2.物理与材料科学学院，安徽合肥230601）

随机游走是研究随机过程的一类重要模型[1]。早在1905 年，Karl Perason 在《Nature》杂志上就提出了随机游走这个名词[2]。同年，Albert Einstein发表了一篇研究悬浮在液体中的布朗粒子随机运动的文章，并导出了著名的涨落耗散定理[3]。至此，随机游走的理论研究不仅推动了许多学科的发展，如概率论、计算科学、统计物理等，而且应用到了很多实际问题中，如动物的迁徙和觅食[4]，神经元放电动力学[5]，高分子、细胞等生命组织在复杂环境中的扩散过程[6]，PaegRank排序算法[7]，金融市场的模拟等[8]。复杂网络是描述自然界大量复杂系统的有用模型，如社交网络、万维网和蛋白质相互作用网络等[9]。复杂网络上随机游走的研究日益增多[10]，不仅包括在任意网络上稳态占据概率和平均首达时间等重要量的推导，以及标度行为和图谱特性的关系等[11-13]，还包括在网络实际问题中的应用研究，如计算机网络上路由策略[14]、社团结构[15]、核心边缘结构[16]等中尺度结构划分，排序[17]、链路预测[18]、传播[19]、观点动力学等问题[20]。

目前，大部分研究关注的是无记忆的马尔可夫游走过程，即游走者下一时刻的位置只依赖当前位置而与之前所处的位置无关。然而，基于对人类出行、船运等实证数据的研究都表明，实际的扩散过程是非马尔可夫的[21-22]。本文研究一类特殊的非马尔可夫随机游走模型——非回溯随机游走。该模型中游走者具有短期记忆效应，他能够记住上一时刻所处节点并要求不能立刻返回该节点。通过定义二阶节点（即网络中一条有向边），可以将该模型转为马尔可夫过程来研究。在这个二阶马尔可夫模型中，游走者的转移概率是依赖于网络的非回溯矩阵。

1 模型定义

在一般的随机游走（RW）模型中，定义t时刻一个游走者处于节点i，在t+1时刻该游走者随机扩散到的节点i的一个近邻节点j，该随机过程属于马尔可夫过程。而在非回溯随机游走中（NRM），游走者从他所在的节点随机游走到一个近邻节点，但不能立刻返回。例如，t-1时刻游走者处于节点i，t时刻游走者从节点i游走到节点j，t+1时刻该游走者随机游走到节点j的一个近邻节点，但不包括节点i，该随机过程是非马尔可夫的。该模型可以利用二阶马尔可夫模型来代替[23]，如图1所示。为此，定义二阶节点为ij，即表示在相邻的时刻粒子从节点i游走到节点j。记粒子的转移概率为Wij,lk，即表示在相邻时刻游走者从二阶节点ij转移到二阶节点lk的概率。对非回溯随机游走，

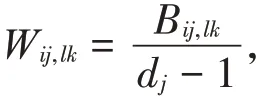
其中，Bij,lk是网络的非回溯矩阵元，已在网络渗流[24]、中心性[25]和社团划分[26]等问题中发挥着重要的作用，其定义为Bij,lk=δjl( )1-δik，其中，δij为克罗内克符号：当i=j 时，δij=1；当i ≠j 时，δij=0。因此，仅当j=l和i ≠k时，非回溯矩阵元Bij,lk=1；否则，Bij,lk=0。dj是节点j的度，即节点j的最近邻的邻居数目。

图1 非回溯随机游走的二阶马尔可夫表示图

2 结果分析

定义Pij( t )为t时刻游走者处于二阶节点ij的占据概率。Pij( t )满足主方程：矩阵形式：P( t+1 )=P( t )W，其中，P={ Pij}为2×E 维行向量，E 为网络的边数目。当t →∞，占据概率达到稳态，Ps=P( ∞)，满足方程P( ∞ )=P( ∞)W。可以看出，Ps是转移矩阵W的特征值为1时所对应的左特征向量。不难验证，转移矩阵W满足行和、列和都为1（双随机矩阵），特征值1对应的左特征向量为( 1,1,1,…,1 )，归一化得。定义Pis为节点i的稳态占据概率，

这个结论和一般的随机游走是相同的，即稳态时占据某一节点的概率正比于该节点的度[11]。为了验证这一结论，我们在不同的网络上模拟非回溯随机游走，并统计每个节点的占据概率。我们使用了两个Barabasi-Albert（BA）网络和两个无标度网络（SFN），其中后者通过配置模型生成[9]。对BA网络，平均度=4，网络大小分别为N=1000和N=5 000。对SFN，最小度kmin=2，网络大小N=10 000，度分布幂律指数分别为γ=2.5和γ=3.5。图2展示了理论结果（线）和模拟结果（点），可以看出，模拟和理论完全吻合。

在随机游走的研究中，一个重要的物理量是首达时间，即游走者从节点i出发，第一次到达节点j的时间称为从节点i 到节点j 的首达时间。显然，首达时间是一个随机量，它的期望值就是平均首达时间（MFPT）。从节点i到节点j的平均首达时间记为Ti,j。类似地，定义Tmi,j为从二阶节点mi出发，首次到达节点j的平均时间。Tmi,j满足递归方程

进一步，得到从节点i出发，首次到达节点j( j ≠i)的平均时间

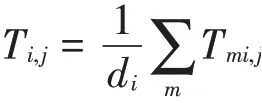
和从节点i出发、首次返回到节点i的平均时间

图3给出了一个平均度为4，节点数目N=30的BA无标度网络（图3（a））上非回溯随机游走的平均首达时间的理论结果和模拟结果（图3（b））。可以看出，理论结果和模拟结果吻合得非常好，平均首达时间按到达节点的度呈现台阶的分布。也就是说，平均首达时间主要依赖于到达节点的度，到达节点的度越大，平均首达时间一般也越短。为比较起见，图3（c）给出了一般随机游走的平均首达时间的理论和模拟结果。与非回溯随机游走相比，一般随机游走的平均首达时间要更长，同样呈现类似的台阶分布，但涨落变大了。

图3 (a)BA网络；(b)非回溯随机游走的平均首达时间；(c)一般随机游走的平均首达时间

下面计算全局平均首达时间（GMFPT），即平均首达时间对出发节点稳态占据概率的统计平均，其定义为

图4给出了前述4个网络上非回溯随机游走和一般随机游走的全局平均首达时间随节点度的分布图。一方面，无论哪种网络非回溯随机游走的全局平均首达时间都要比一般随机游走的全局平均首达时间短，这意味着非回溯随机游走的搜索效率更高。另一方面，对度大小相同的节点，非回溯随机游走全局平均首达时间涨落非常小，也就是说，非回溯随机游走中全局平均首达时间更严格地依赖于到达节点的度。而对一般随机游走，度相同的节点的全局平均首达时间的涨落比较大。对度相同节点的全局平均首达时间作平均，在双对数坐标下全局平均首达时间随节点度可以很好地拟合成一条直线。我们发现两种情况下，直线的斜率都为-1，即全局平均首达时间按∼k-1j的规律变化。

图4 非回溯随机游走和一般随机游走的全局平均首达时间随节点度的变化图

非回溯随机游走和一般随机游走的覆盖时间定义为从某个节点出发，遍历网络所有节点的时间，记C(i)为从节点i 出发的覆盖时间。覆盖时间C(i)多次随机游走的平均，称为平均覆盖时间，记为。图5 给出了前述4 种不同网络中非回溯随机游走和一般随机游走的平均覆盖时间随节点的变化，可以看出：（1）平均覆盖时间不显著依赖出发节点；（2）非回溯随机游走的平均覆盖时间要比一般随机游走的少。将平均覆盖时间对节点的占据概率做平均，即得到网络平均覆盖时间的期望值，如图5中横线所示。

图5 非回溯随机游走和一般随机游走的平均覆盖时间随节点编号的变化图

3 结束语

本文通过定义二阶节点的方法，将具有短期记忆效应的非回溯随机游走模型转化为马尔可夫过程来研究，严格推导出非回溯随机游走的稳态占据概率的表达式，表明了稳态占据概率与节点度成正比的结论，这与一般随机游走的结论是一致的；推导出任意两个节点之间平均首达时间的计算公式。与一般随机游走比较，非回溯随机游走的平均首达时间要短，且更依赖于到达节点的度。最后计算了全局平均首达时间和平均覆盖时间，无论是非回溯随机游走还是一般随机游走，全局平均首达时间都是按节点度的负一次方衰减，平均覆盖时间不依赖于节点的度。我们的研究表明，非回溯随机游走比一般的随机游走具有更高的搜索效率。因此，非回溯随机游走在网络路由、搜索和分类问题中具有潜在的应用价值。