广东 薛新建

著名数学家华罗庚用“由薄到厚”和“由厚到薄”两个基本过程，形象地解释了知识框架和解题训练之间的辩证关系.“由薄到厚”是学习接受、加强积累、构建知识框架、奠实“四基”的过程；“由厚到薄”则是消化提炼、探索本质、回归知识框架、提升“四能”的过程.波利亚在《怎样解题》中把解题的第一步制定为“弄清问题”，即对问题产生的知识背景进行精准定位,用知识框架的整体视角看待问题，再对题目的条件和设问，从不同角度关联运用相关知识，进行有目标的转化.于涛老师认为，解题的核心就是知识的联系与模型的识别.正确的解题训练可以发掘知识之间隐含的关联性，使知识框架进一步强化和完善，并提高数学模型的适用性.解题的出发点和落脚点回归知识本身，才能引导学生把握数学内容的本质，形成和发展核心素养，符合《普通高中数学课程标准(2017年版2020年修订)》(下称“新课标”)的基本理念.

下面就以平面向量“双参最值问题”为例，对高三解题训练的高效模式进行探究.

一、典例引入，定位剖析

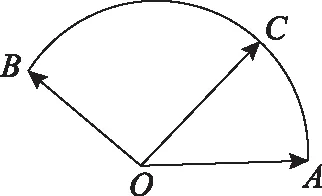
这是一道经典的向量高考原题，2017年全国卷Ⅲ还将相同问题以圆的形态再次考查.平面向量作为高中数学重要的工具性内容，兼具数形两种形态，与其他章节例如三角函数、解析几何、立体几何、参数方程等知识都有交汇，是高考考查的热门考点.本题以极具数学之美的几何图形扇形作为背景，以简洁精炼的向量符号形式给出条件，形数兼备，又引出二元函数最值问题，借以考查函数思想.题目涉及向量知识模块如相等向量、向量运算、向量坐标等基础知识，和其他知识模块如基本不等式、线性规划、解三角形等初等知识，并可引申出拉格朗日乘数法等高等知识，丰富的知识面跨度，给不同层次的学生提供了足够的发挥空间.题目体现的消元、化归与转化、函数与方程等数学思想和方法，以及考查的逻辑推理、数学建模、数学运算、数学抽象等诸多核心素养，都具有极高的推广和研究价值.

定位1【向量运算】条件是向量表达式，问题是两个实数和的形式，回顾向量知识框架中，哪一部分可以实现向量向实数的转化？不难想到向量的运算中，求数量积或者求模(平方)，都可以将向量关系实数化，为本题提供突破思路.

定位1.1【向量求数量积】如图，设∠AOC=α，则

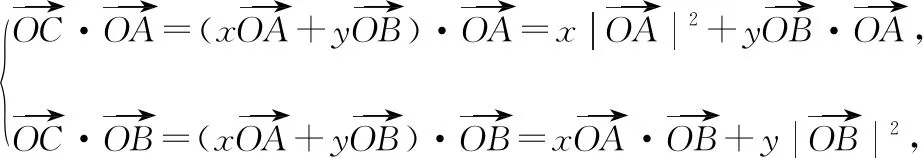
至此完成向量关系实数化，由于α的引入，得到的x和y的关系属间接关系，即参数方程关系，只需通过消元将二元函数最值问题转化为一元函数最值问题即可解决问题.

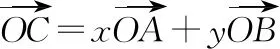
定位2【二元函数最值问题】从函数知识模块中提取出如图所示的解决二元函数最值问题的基本方法框架，由于题中x，y的等量关系消元和画图比较困难，本题优先选用基本不等式进行计算.

定位2.3【拉格朗日乘数法】高等数学里的拉格朗日乘数法能够把约束优化问题很好地转化为无约束优化问题，这里可以根据学生基础加以引申，也可以点到为止为学生将来进入大学学习高数预留伏笔.

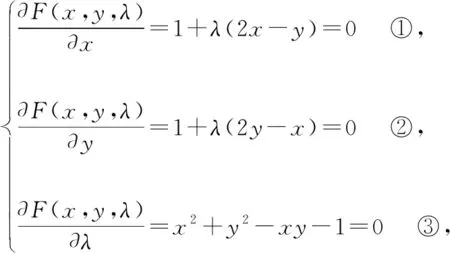
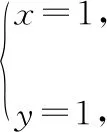
定位3【相等向量的概念】条件中的向量表达式可以看作一个向量的等量关系，“相等向量”从属于向量的基本概念知识板块，其具有几何和代数(坐标法)两种基本形态，能不能从中找到系数间的等量关系呢？利用代数(坐标法) 形态可以达到这个目的.

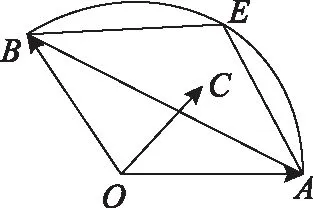
定位3.1【相等向量的坐标形式】如图，以O为坐标原点，OA为x轴正半轴建立平面直角坐标系，

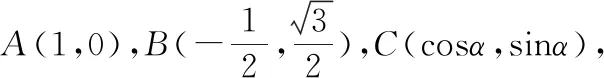
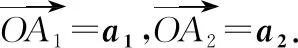
② 设a=(x1,y1),b=(x2,y2)，则a±b=(x1±x2,y1±y2)；λa=(λx1,λy1)；a//b⟺x1y2-x2y1=0；

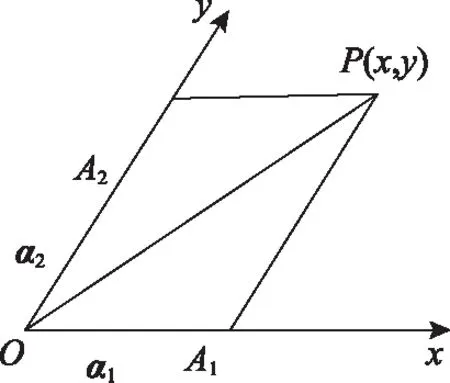
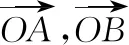
斜坐标系是对直角坐标系进一步的推广，由于建系要求低而具有广泛的适用性.在斜坐标系下向量表达式坐标化后实现实数化的目标，思路清晰、计算简洁，再借助线性规划的思想方法解决最优问题，在平面向量双参最值问题与一般的二元函数最值问题间搭起了一座新的桥梁.实际上，斜坐标系可以方便地解决两个实系数x,y任意线性组合的最值问题，只需要根据题目调整一下基底即可.

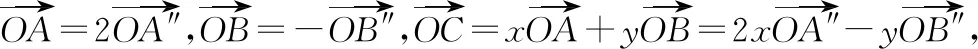
二、形成框架，提升思维

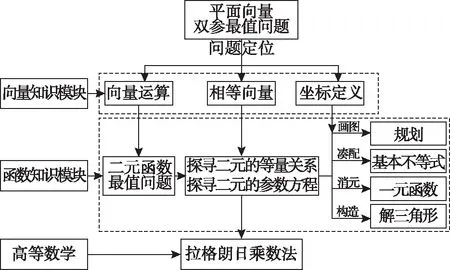
通过前述思考我们发现，平面向量双参最值问题可以定位到平面向量知识模块中的“向量运算”、“相等向量”和“坐标定义”三个小的知识点.“向量运算”中的“数量积”以及“模”的计算，都可以实现向量关系实数化，从而将平面向量双参最值问题转化为二元函数最值问题，二元函数最值问题从属于函数知识模块，具有自身的一套解决体系，因此后续思路按照二元函数最值问题的方法框架就可以推进下去；“相等向量”概念的代数形式(坐标化)则把题目条件导向二元函数最值问题的下一步，即“探寻二元等量关系”；“坐标定义”的问题定位引发我们对斜坐标系的引入，使得问题直接转入广义规划解决问题，这符合二元函数求最值问题下属的一种具体情况.通过上述思考，我们将平面向量双参最值问题在向量和函数两个知识模块之间做如下架构.

三、推而广之，反思教学

上述对数学问题的探索模式在高三复习中具有很大的推广价值，具体说来有如下实际意义：

将问题在知识框架中定位可以促进学习者看清其数学本质.数学问题千变万化，问题的解法多种多样，如果教师只是就题论题或者就题论法，必然会陷入无限题海，失去方向.如果学习的过程中能够将问题回归知识框架，以有限的知识框架去界定无限的问题类型，就可以从不同的视角对问题进行剖析，最终看清问题的本质，实现问题的“归一”.

用知识框架统领解题训练，学习者才会有思维的提升.知识框架具有系统性、远见性和可发展性，将平时的解题训练建立在知识框架之上，学习者才能理解巧妙思路的来源，激发寻找更多思路的灵感，实现思路之间的优劣比较从而实现思维的提升，进而对知识框架进行完善和重构，使知识框架得以补充和发展.而忽略知识框架，片面追求兵来将挡水来土掩式的解题训练，则会把知识碎片化，即使短期内颇具效果，从长远来看，会把数学的学习变成机械教条的死记硬背，学习者缺乏思维的训练和提升，感受不到数学的美感和成就感，渐渐也会失去学习的兴趣.