李兴

[摘  要] 空间向平面的转换是突破立体几何问题的基本策略，也是降维思考的方法途径，其中翻折问题、截面问题、角度问题是最具代表性的空间问题. 文章以三大问题为例，详细解析空间向平面转换的方法技巧.

[关键词] 空间几何;平面;转换;翻折;截面;角度

背景综述

立体几何是高中数学的重点内容，分析判定几何要素的位置关系、计算推理空间图形的几何量是常见的问题类型，问题突破的一般思路是降维分析，即把握空间图形与平面几何之间的关联，实现两者的转换，从而完成空间问题的平面化解答. 因此对学生的空间思维有着较高的要求，需要有效实施降维转换，合理构建思路. 降维转化体现最为明显的三类问题为翻折问题、截面问题、角度问题，下面结合实例探究总结方法技巧.

示例探究

一、把握不变量，突破几何翻折

图形翻折是空间几何的典型问题，在翻折的过程中，图形经历了由平面到空间的构建过程，在该过程中两者显然存在紧密的联系，即翻折前后有一定的不变量，而这些不变量构建了平面图形与空间几何之间的桥梁，也是问题降维突破的关键.

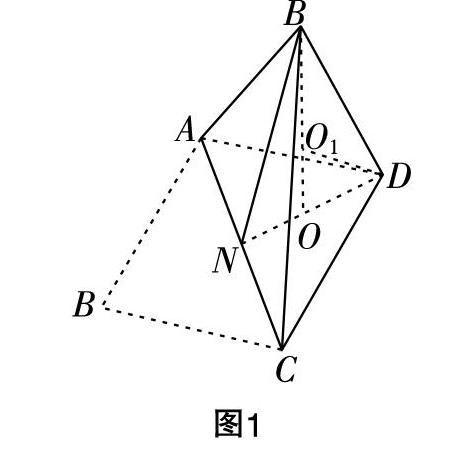
例1：已知菱形ABCD的边长为2，BD=2■，现将菱形ABCD沿着对角线AC进行对折，使得二面角B-AC-D的余弦值为■，如图1所示，试求所得三棱锥A-BCD的外接球的表面积.

解析：本题目中翻折过程为：菱形ABCD沿对角线AC翻折为三棱锥，关键条件为二面角B-AC-D的余弦值为■. 分析可知图形翻折过程菱形所具有的一些特性保持不变，故可从中提取一些不变量，然后以此为基础，结合对应二面角来推理核心条件，进而求解三棱锥外接球的半径.

BD为菱形的一边对角线，分析可知△ABC和△ADC为等边三角形，取AC的中点为N，连接ND，BN，则BN⊥AC，DN⊥AC，所以∠BND就为二面角B-AC-D的平面角. 过點B作ND的垂线，垂足为点O，则BO⊥平面ACD，如图1所示. 易知BN=DN=■，cos∠BND=■，可得ON=BN·cos∠BND=■=■ND，即点O为△ADC的中心，OB=■. 而三棱锥A-BCD的外接球的球心必然位于BO所在直线上，可将球心设为O■，半径为r，连接DO■，则BO■=DO■=r，OO■=■-r，在Rt△OO■D中，由勾股定理可得DO■=OO■+OD2，所以■-r2+■2=r2，可解得r=■，则三棱锥外接球的表面积为S=4πr2=6π.

指点迷津：上述是以平面折叠为背景的空间几何问题，求解过程充分利用了菱形的边长相等、对角线垂直平分等特性，以此为基础确定了外接球的半径. 其中的垂直关系是进行问题推理的关键，也是平面几何与空间立体的衔接条件，因此在突破折叠类立体几何问题时，需要把握折叠前后的不变量，利用恒定关系开展推理分析. 另外实际求解时可以按照如下步骤进行：

第一步，根据题干信息理解折叠过程，提取其中的折叠条件;

第二步，根据平面图形的特性，提取平面几何与空间几何的不变量;

第三步，根据不变量开展分析推理，进行空间转换，降维思考;

第四步，在平面中建立解析模型，计算关键量，完成求解.

二、提取分析图形，突破截面问题

分析空间图形中的截面要素是常见的问题类型，也是空间与平面转换视角下的典型问题. 该类问题往往以常见的立体图形为基础，通过图形组合来构建复合图形，以平面截取的方式来构建相应的截面问题，如截面的面积、截面周长、截面的棱长等. 空间转换时需要明确切点及接点的位置，提取截面图形，进而结合相关知识分析推理.

例2：三棱锥S-ABC的所有顶点均位于球O的球面上，已知SA⊥平面ABC，△ABC为等腰直角三角形，其中SA=AB=AC=2，点D为BC上的中点. 现过点D作球O的截面，试求截面图形面积的最小值.

解析：本题目为空间几何求截面面积问题，显然需要完成空间向平面的转换，过点D作球O的截面，显然截面始终为圆，故截面面积由圆的半径决定. 已知△ABC为等腰直角三角形，其中点D是斜边BC上的中点，则点D就为△ABC的外心，过点D作DO⊥平面ABC，则DO上的点到点A，B，C的距离相等，故球心位于直线OD上. 又知SA⊥平面ABC，SA=2，故当DO=■SA=1时，点O为外接球的球心.

过点D作球O的截面，显然点D就为截面圆的圆心，分析可知可将截面圆的半径表示为r=■，其中h表示球心O到截面的距离，显然当h最大时，截面圆的半径最小，此时截面的面积也最小，故正确的解法是确保OD⊥截面，在该情形下进行如下推理计算.

连接OA，如图2所示，设外接球的半径为R，在直角梯形SADO中，OA=OS=R，SA=2，OD=1，AD=■，可解得R=■. 在Rt△OAD中，由勾股定理可得AD=■=■，即截面圆最小半径为■，所以截面面积的最小值为2π.

指点迷津：上述以三棱锥外接球为背景，开展截面面积最值分析，问题突破的关键有两点：一是确定截面图形，二是确定截面图形半径最小时的截取情形. 对于空间几何截面问题的转换，需要具备较强的空间想象力，对几何体的特征结构有充分的了解. 以涉及球的外接情形为例，问题突破分为两个阶段：一是模型构建，平面转换;二是几何应用，化简求解.

第一阶段，需把握图形的切点或接点，构建相应的截面模型，从而将空间问题转换为相应的平面几何问题;

第二阶段，该阶段需要利用平面几何的性质定理来解析模型，可以综合利用三角函数、均值不等式、导数、方程等知识.

三、空间向量转换，突破角度计算

立体几何中的角度计算是核心问题，求解过程需要将空间角转化为平面角，故完成空间到平面的转换十分重要，也是问题突破的难点所在. 转换时可以采用多种方法，结合定义，利用共垂面法，也可直接使用空间向量法，其中向量法的程序性更强，可直接将问题转换为平面内法向量的夹角问题.

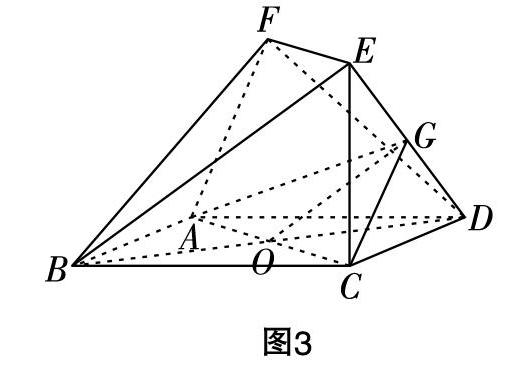
例3：如图3所示，在多面体ABCDEF中，已知四边形ABCD为菱形，EF∥AC，EF=1，∠ABC=60°，CE⊥平面ABCD，CE=■，CD=2，点G为DE的中点.

（1）试求证平面ACG∥平面BEF;

（2）试求直线AD与平面ABF所成角的正弦值.

解析：本题目为常规的空间几何题，第（1）问两平面平行证明，利用定理逐步证明即可;第（2）问为直线与平面所成角计算，可以采用空间向量法.

（1）连接BD，与AC的交点为O，可知点O为BD的中点，则OG∥BE，由于BE？奂平面BEF，OG位于平面BEF外，故OG∥平面BEF;

又知EF∥AC，AC∥平面BEF，AC与OG的交点为O，平面ACG内有两条相交直线分别与平面BEF平行，所以平面ACG∥平面BEF.

（2）以点O为坐标原点，分别以OC，OD，OF为x，y，z轴建立空间直角坐标系，如图4，则A（-1，0，0），B（0，-■，0），D（0，■，0），F（0，0，■），则■=（1，■，0），■=（1，-■，0），■=（1，0，■）.

设平面ABF的法向量为m=（a，b，c），由题意可知m⊥■，m⊥■，

则有a-■b=0，a+■c=0，可解得a=■，b=1，c=-1，即m=（■，1，-1），所以cos〈■，m〉=■=■，所以直线AD与平面ABF所成角的正弦值为■.

指点迷津：空间角度问题的基本求解思路就是空间转换，即将其转化为平面中的角度问题，求解方法具有一定的代表性，可利用定义法、三垂线定理、射影法、向量法.

对于其中的异面直线所成角问题，可以按照如下思路进行：第一步平移，化异面为相交;第二步定角，根据角定义找到所成的平面角;第三步求角，在三角形中使用余弦或正弦定理求角.

而利用空间向量法求解时则可以省去平移、定角的过程，直接遵照如下思路进行：

第一步建系，根据图形特点，合理建立空间直角坐标系;

第二步列向量，根据题干线段长，计算关键点坐标，然后由点坐标求相应直线的方向向量;

第三步求法向量，利用直线垂直对应数量积为零来列方程组，求解法向量;

第四步求角，將空间内的角度问题转换为法向量的关系问题，完成角度求解.