测度微分方程的Lipschitz稳定性
2020-09-21李宝麟
李宝麟,席 娅
(西北师范大学数学与统计学院,甘肃 兰州 730070)
1 引言
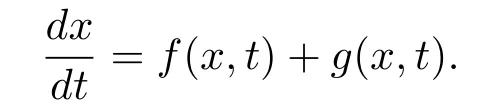
如果扰动项g(x,t)是连续可积的,那么受扰动之后的系统仍旧是常微分方程,它的解仍旧是连续的,如果扰动项是脉冲型的,那么扰动之后系统的状态就不会随着时间连续变化而变化,而是呈现出一种瞬时状态.为了研究这类问题,我们对上述方程加上一种脉冲型的扰动,这就给出如下形式的方程

其中Dx和Du分别表示函数x和u的分布导数.形如(1.1)的方程叫做测度微分方程.由于测度微分方程的解没有连续性,又没有随机系统那么复杂,因此,我们可以说测度微分方程是一种不同于经典不连续系统的新的不连续系统.测度微分方程已经被很多学者研究(见文献[1–4]).
在文[5]中Dannan和Elaydi研究了常微分方程的Lipschitz稳定性;文[6]中作者讨论了一类脉冲微分系统的Lipschitz稳定性;文[7]中作者给出了脉冲泛函微分方程的Lipschitz稳定性;文[8]中作者建立了广义常微分方程的变差一致Lipschitz稳定性,一致Lipschitz稳定性和一致整体Lipschitz稳定性,并通过滞后型脉冲微分方程在一定条件下与广义常微分方程的等价关系,讨论了滞后型脉冲微分方程的Lipschitz稳定性.本文是在文[8]的基础上,通过测度微分方程与广义常微分方程的等价关系,定义了测度微分方程

和扰动后的测度微分方程

的变差一致Lipschitz稳定性,一致Lipschitz稳定性和一致整体Lipschitz稳定性,并建立了测度微分方程和扰动后的测度微分方程的Lipschitz稳定性定理.方程(1.2)和方程(1.3)的等价方程为
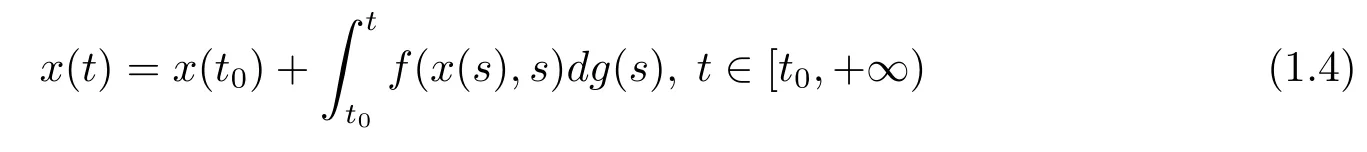
和
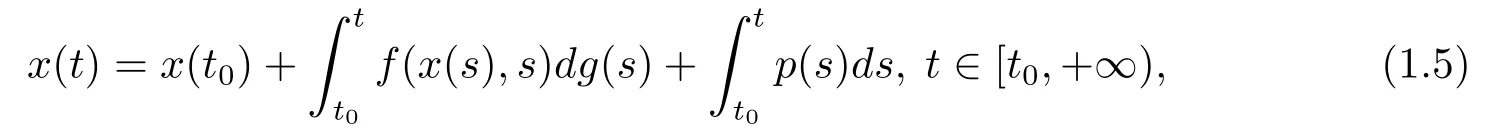
其中f:Bc×[t0,+∞)→Rn,Bc={y∈Rn,‖y‖<c},g:[t0,+∞)→R,p:[t0,+∞)→Rn是比Lebesgue-Stieltjes可积更广泛的Kurzweil-Henstock-Stieltjes可积函数和Kurzweil-Henstock可积函数(见文[10]).
函数x:[a,b]→Rn为[a,b]上的正则函数是指若函数x的左右极限
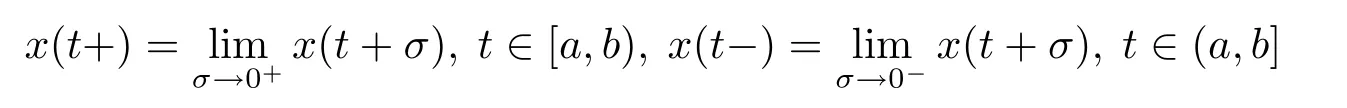
分别存在且有限(正则函数在有限区间上有界,在无穷区间上不一定有界).记G*([a,b],Rn),[a,b]⊂[t0,+∞)是定义在[a,b]上的正则函数全体,并且是左连续的.G*([t0,+∞),Rn)为关于函数x:[t0,+∞)→Rn的一个向量空间,使得对所有[a,b]⊂[t0,+∞),x|[a,b]属于空间是关于所有x∈G*([t0,+∞),Rn)的一个向量空间,使得
记Ω=Bc×[t0,+∞),本文假定函数f:Ω→Rn,g:[t0,+∞)→R,p:[t0,+∞)→Rn满足下列条件
(H1)函数g:[t0,+∞)→R在[t0,+∞)上是不减的左连续函数.
(H2)对每一个x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),Kurzweil-Henstock-Stieltjes积分存在.
(H3)存在一个关于g的局部Kurzweil-Henstock-Stieltjes可积函数M:[t0,+∞)→R+,使得对任意的x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),s1<s2,
(H4)存在一个关于g的局部Kurzweil-Henstock-Stieltjes可积函数L:[t0,+∞)→R+,使得对任意的x,,s1,s2∈[t0,+∞),s1<s2,
(H5)对每一个x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),Kurzweil-Henstock积分存在.
(H6)存在一个局部Kurzweil-Henstock可积函数N:[t0,+∞)→R+,使得对任意的x∈G*([t0,+∞),Rn),s1,s2∈[t0,+∞),s1<s2,
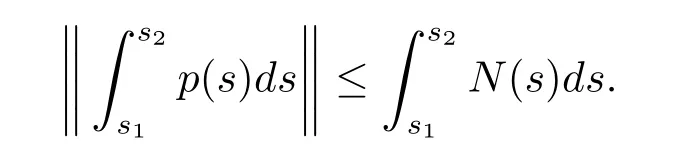
本文主要分为三个部分.第二部分给出了本文所需要的一些定义和引理,第三部分定义了测度微分方程和扰动后的测度微分方程的变差一致Lipschitz稳定性,一致Lipschitz稳定性和一致整体Lipschitz稳定性,并建立了测度微分方程和扰动后的测度微分方程的Lipschitz稳定性定理.
2 预备知识
本节介绍了广义常微分方程的相关定义和引理及测度微分方程与广义常微分方程的等价关系.
定义2.1[9]称函数U:[a,b]×[a,b]→Rn在区间[a,b]上Kurzweil可积,如果存在I∈Rn,使得对任意的ε>0,存在正值函数δ:[a,b]→(0,+∞),使得对[a,b]上的任何δ(τ)-精细分划D={(τj,[αj-1,αj]),j=1,2,···,k},其中τj∈[αj-1,αj]⊂[τj-δ(τj),τj+δ(τj)],有

称I为U在[a,b]上的Kurzweil积分,记作特别地,当U(τ,t)=f(τ)g(t)时,
定义2.2[9]设函数F:Ω→Rn,如果对所有的t∈[α,β],(x(t),t)∈Ω,且对任意的s1,s2∈[α,β],有等式成立,则称x:[α,β]→Rn是广义常微分方程

在区间 [α,β]⊂[t0,+∞)上的解.
定义2.3[9]设不减函数h:[t0,+∞)→R,函数F:Ω→Rn属于函数族F(Ω,h),是指F满足以下条件:对任意的(x,s1),(x,s2)∈Ω,有
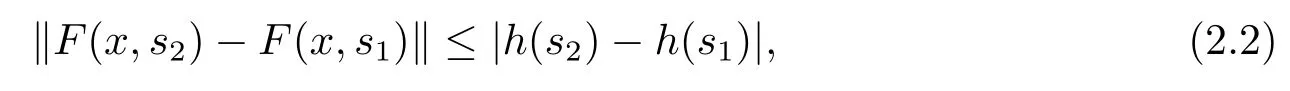
且对任意的(x,s1),(x,s2),(y,s1),(y,s2)∈Ω,有

引理 2.1[9]设F:Ω→Rn满足(2.2)式,如果x:[α,β]→Rn,[α,β]⊂[t0,+∞)是方程(2.1)的一个解,则x在 [α,β]上有界变差,且并且在 [α,β]上x与函数h具有相同的连续性,其中表示x在[α,β]上的全变差.
引理2.2[10]假设f:Ω→Rn满足条件(H2),(H3),(H4),并且g:[t0,+∞)→R满足条件(H1),对任意的τ0∈[t0,+∞),并且定义函数F:Ω→Rn为
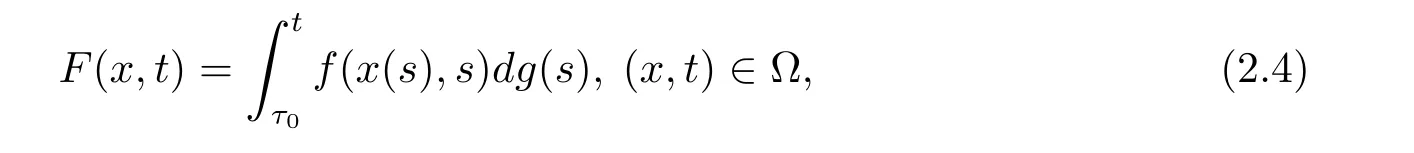
则F∈F(Ω,h),其中h:[t0,+∞)→R是不减的左连续函数,且
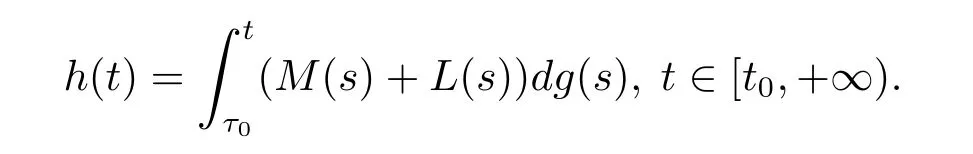
引理2.3[11]假设f:Ω→Rn满足条件(H2),(H3),(H4),并且g:[t0,+∞)→R满足条件(H1),且p:[t0,+∞)→Rn满足条件(H5)和(H6),对任意的τ0∈[t0,+∞),并且定义函数G:Ω→Rn为
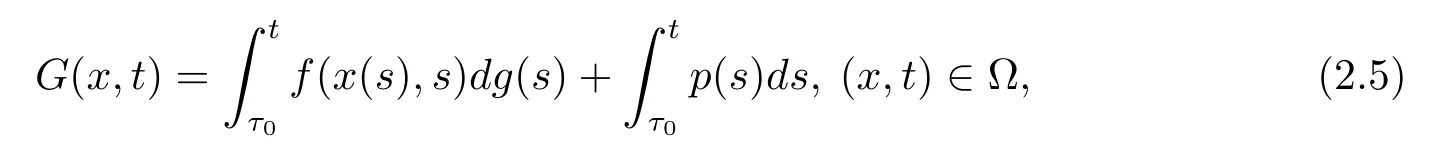
则G∈F(Ω,h),其中h:[t0,+∞)→R是不减的左连续函数,且
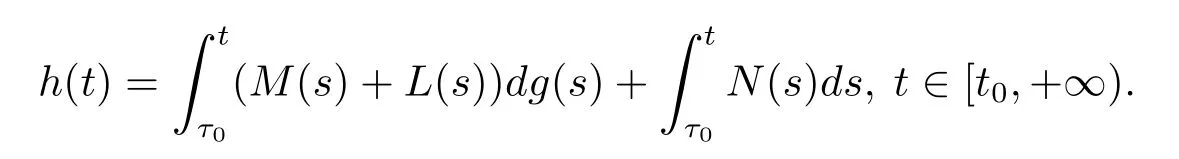
引理2.4[10]假设f:Ω→Rn满足条件(H2),(H3),(H4),并且g:[t0,+∞)→R满足条件(H1),如果函数x:[a,b]→Rn,[a,b]⊂[t0,+∞)是测度微分方程(1.2)的解,当且仅当x是广义常微分方程

在[a,b]上的解,其中函数F由(2.4)式给定.
引理2.5[11]假设f:Ω→Rn满足条件(H2),(H3),(H4),并且g:[t0,+∞)→R满足条件(H1),且p:[t0,+∞)→Rn满足条件(H5)和(H6),如果函数x:[a,b]→Rn,[a,b]⊂[t0,+∞)是测度微分方程(1.3)的解,当且仅当x是广义常微分方程

在[a,b]上的解,其中函数G由(2.5)式给定.
引理 2.6[9]设F∈F(Ω,h),假设x:[α,β]→Rn,[α,β]⊂[t0,+∞)在 [α,β]上是有界变差函数,使得对每一个s∈[α,β],(x(s),s)∈Ω,则积分存在.
引理2.7[9]设F∈F(Ω,h),假设V:[t0,+∞)×Rn→R+是使得对任意的y∈Rn,函数V(·,y):[t0,+∞)→R+在(t0,+∞)上是左连续的,假设以下条件成立
(i)对任意的(t,x),(t,y)∈[t0,+∞)×Rn,常数L>0,有|V(t,x)-V(t,y)|≤L‖x-y‖.
(ii)存在一个实函数Φ:Rn→R,使得对于广义常微分方程(2.6)在区间(a,b)⊂[t0,+∞)上的每一个解y:(a,b)→Rn,对于t∈(a,b),有
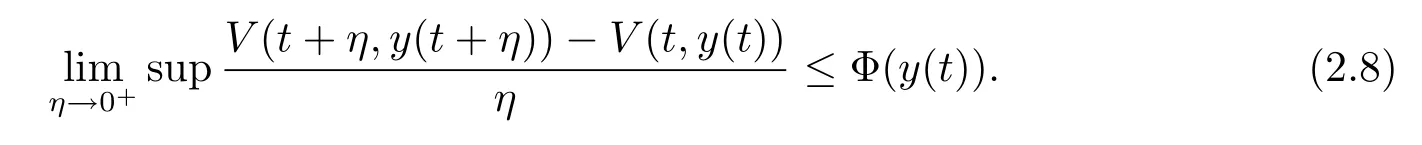
若:[α,β]→Rn,t0≤α<β<+∞是区间 [α,β]上的有界变差函数,并且在 (α,β]上是左连续的,则不等式
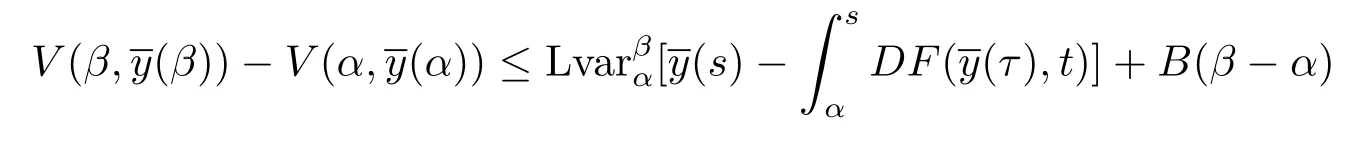
引理2.8[9]设G∈F(Ω,h),假设V:[t0,+∞)×Rn→R+是使得对任意的y∈Rn,函数V(·,y):[t0,+∞)→R+在(t0,+∞)上是左连续的,假设以下条件成立:
(i)对任意的(t,x),(t,y)∈[t0,+∞)×Rn,常数L>0,有|V(t,x)-V(t,y)|≤L‖x-y‖.
(ii)存在一个实函数Φ:Rn→R,使得对于广义常微分方程(2.7)在区间(a,b)⊂[t0,+∞)上的每一个解y:(a,b)→Rn,对于t∈(a,b),有

若:[α,β]→Rn,t0≤α<β<+∞是区间 [α,β]上的有界变差函数,并且在 (α,β]上是左连续的,则不等式
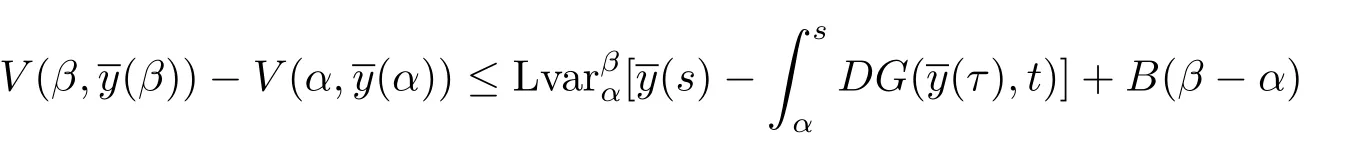
3 主要结果
本节定义了测度微分方程(1.2)及扰动后的测度微分方程(1.3)的变差一致Lipschitz稳定性,一致Lipschitz稳定性和一致整体Lipschitz稳定性.利用广义常微分方程的Lipschitz稳定性结果给出了测度微分方程的变差一致Lipschitz稳定性,一致整体Lipschitz稳定性定理及其证明.
定义3.1测度微分方程(1.2)的平凡解x≡0是变差一致Lipschitz稳定的,若存在A>0,以及δ>0,使得若:[α,β]→Bc,t0≤α<β<+∞是 [α,β]上的有界变差函数,并且在(α,β]上左连续,当(α)‖<δ和

时,则有
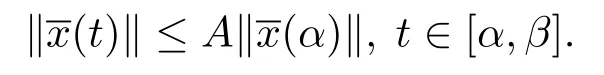
定义3.2测度微分方程(1.2)的平凡解x≡0是
(i)一致Lipschitz稳定的,若存在A>0,δ>0,使得若:[α,β]→Bc,t0≤α<β<+∞是测度微分方程(1.2)在[α,β]上的一个解,当(α)‖<δ时,则(t)‖ ≤(α)‖,t∈[α,β].
(ii)一致整体Lipschitz稳定的,若存在A>0,使得若:[α,β]→Bc,t0≤α<β<+∞是测度微分方程(1.2)在[α,β]上的一个解,则(t)‖ ≤(α)‖,t∈[α,β].
注若测度微分方程(1.2)的平凡解x≡0是变差一致Lipschitz稳定的,则它是一致Lipschitz稳定的.
定义3.3测度微分方程(1.3)的平凡解x≡0是变差一致Lipschitz稳定的,若存在A>0,以及δ>0,使得若:[α,β]→Bc,t0≤α<β<+∞是 [α,β]上的有界变差函数,并且在(α,β]上左连续,当(α)‖<δ和
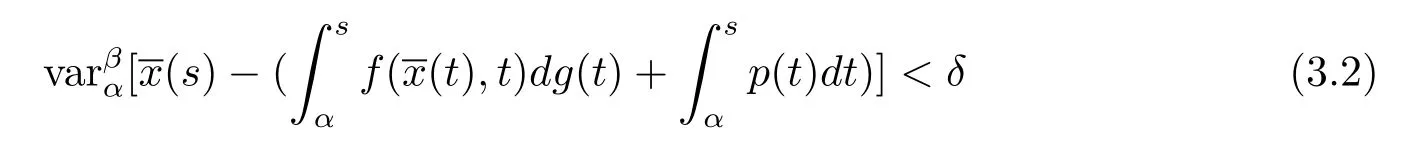
时,则有
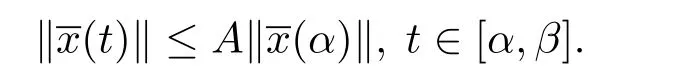
定义3.4测度微分方程(1.3)的平凡解x≡0是
(i)一致Lipschitz稳定的,若存在A>0,δ>0,使得若:[α,β]→Bc,t0≤α<β<+∞是测度微分方程(1.3)在[α,β]上的一个解,当(α)‖<δ时,则
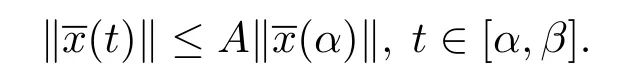
(ii)一致整体Lipschitz稳定的,若存在A>0,使得若:[α,β]→Bc,t0≤α<β<+∞是测度微分方程(1.3)在[α,β]上的一个解,则
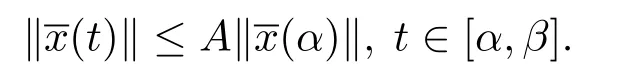
注若测度微分方程(1.3)的平凡解x≡0是变差一致Lipschitz稳定的,则它是一致Lipschitz稳定的.
定理3.1设,其中假设V满足以下条件
(i)对所有的t∈[t0,+∞),有V(t,0)=0.
(iii)存在一个常数K>0,使得
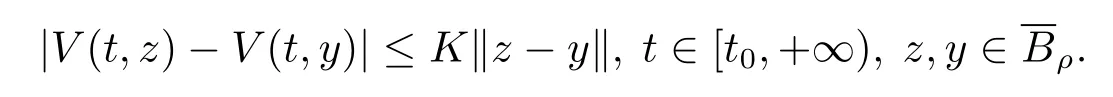
(iv)存在一个单调递增函数b:[0,+∞)→[0,+∞)满足b(0)=0,使得对所有的t∈[t0,+∞),有V(t,x)≥b(‖x‖).

则方程(1.2)的平凡解x≡0是变差一致Lipschitz稳定的.
证根据引理2.2,需验证F∈F(Ω,h),F由(2.4)式给定,Ω=Bc×[t0,+∞).因为f:Ω→Rn满足条件(H2),(H3),(H4),并且g:[t0,+∞)→R满足条件(H1),使得对任意的(x,s2),(x,s1)∈Ω,有

且对任意的(x,s2),(x,s1),(z,s2),(z,s1)∈Ω,由条件(H4),有

所以F∈F(Ω,h),其中τ∈[t,+∞),且h:[t,+∞)→R是000不减的左连续函数.
由引理2.4可知,测度微分方程(1.2)的解也是广义常微分方程(2.6)的解,因此它们的解都是有界变差函数.
以下证明测度微分方程(1.2)的平凡解x≡0是变差一致Lipschitz稳定的.
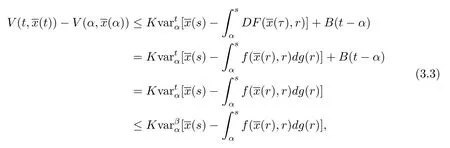
因为Φ≡0,所以且由条件(i)和(iii),有即

对于ε>0,使得不等式成立.设δ>0,使得 2Kδ<b(ε).若

因此由(3.3)和(3.4)式,有

由于2Kδ<b(ε),则有
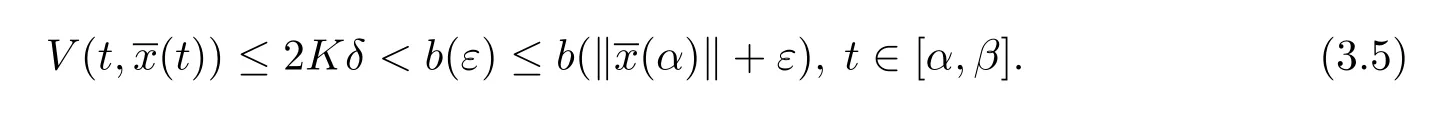
另外,由条件(iv),有
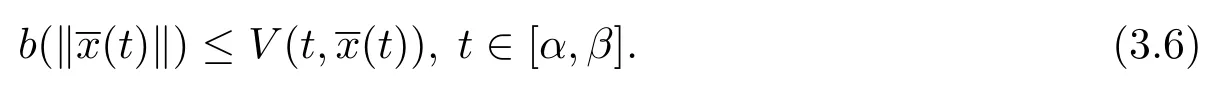
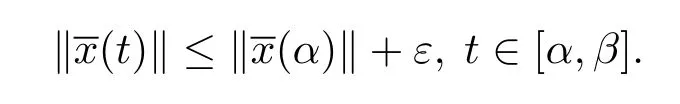
由定义3.1,取A=1,并且由ε的任意性,则满足,则测度微分方程(1.2)的平凡解x≡0是变差一致Lipschitz稳定的.
定理3.2设满足定理3.1中的条件(i),(ii),(iii)和(v),并且满足条件
(iv′)对所有的,有V(t,x)≥‖x‖.
则方程(1.2)的平凡解x≡0是一致整体Lipschitz稳定的.
证设是测度微分方程 (1.2)在 [α,β]上的解.由条件(iii),(v)及引理2.4和引理2.7,其中Φ≡0,所以对任意的t∈[α,β],有
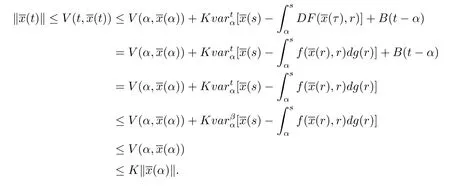
定理3.3设,其中假设V满足以下条件
(i)对所有的t∈[t0,+∞),有V(t,0)=0.
(iii)存在一个常数K>0,使得
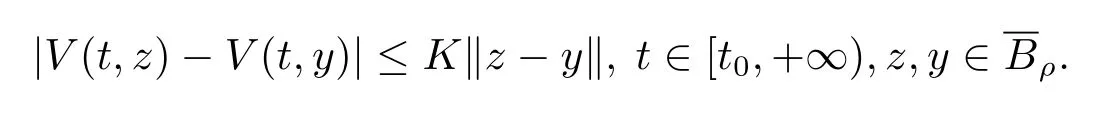
(iv)存在一个单调递增函数b:[0,+∞)→[0,+∞)满足b(0)=0,使得对所有的t∈[t0,+∞),有V(t,x)≥b(‖x‖).
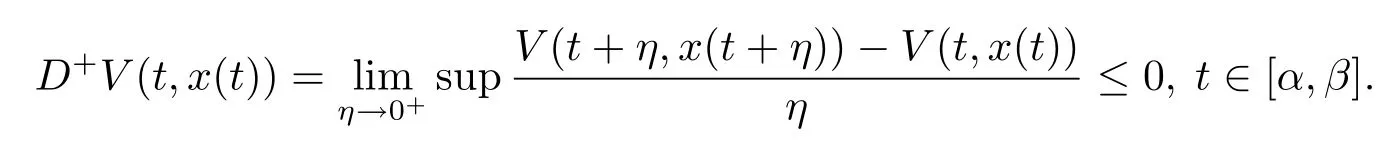
则方程(1.3)的平凡解x≡0是变差一致Lipschitz稳定的.
证根据引理2.3,需验证G∈F(Ω,h),G由(2.5)式给定,Ω=Bc×[t0,+∞).因为f:Ω→Rn满足条件(H2),(H3),(H4),并且g:[t0,+∞)→R满足条件(H1),p:[t0,+∞)→Rn满足条件(H5)和(H6),使得对任意的(x,s2),(x,s1)∈Ω,有
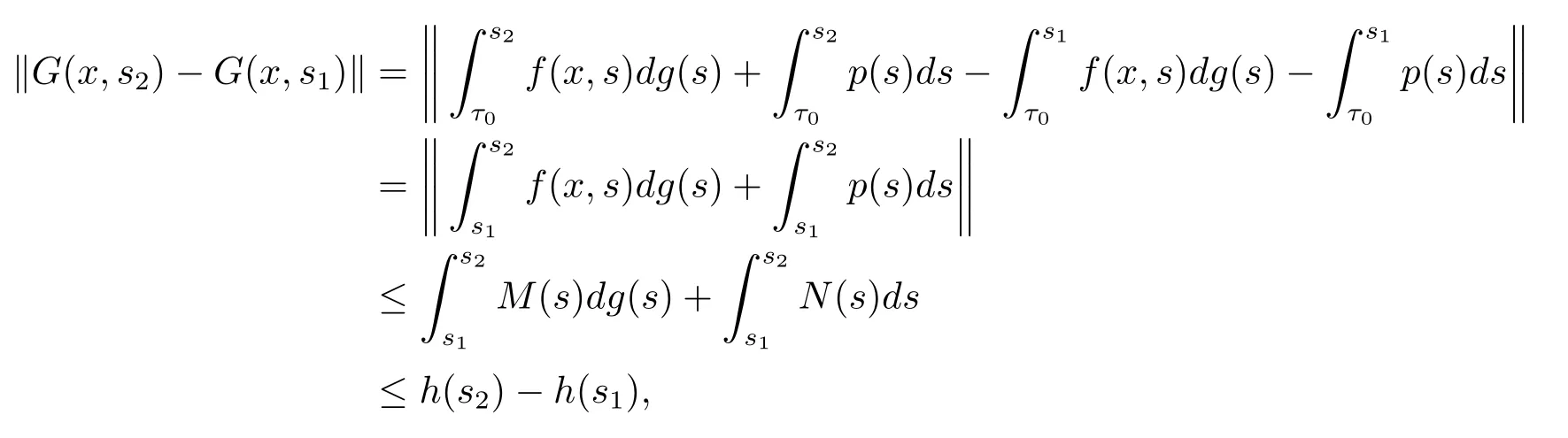
且对任意的(x,s2),(x,s1),(z,s2),(z,s1)∈Ω,由条件(H4),有
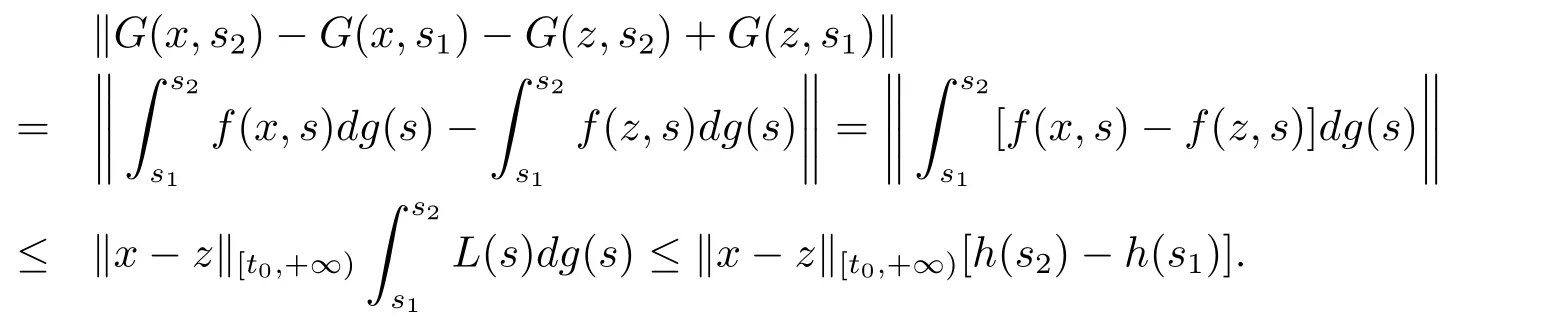
所以G∈F(Ω,h),其中τ0∈[t0,+∞),且h:[t0,+∞)→R是不减的左连续函数.
由引理2.5可知,测度微分方程(1.3)的解也是广义常微分方程(2.7)的解,因此它们的解都是有界变差函数.
以下证明测度微分方程(1.3)的平凡解x≡0是变差一致Lipschitz稳定的.

因为Φ≡0,所以且由条件(i)和(iii),有即

对于ε>0,使得不等式成立.设δ>0,使得 2Kδ<b(ε).若
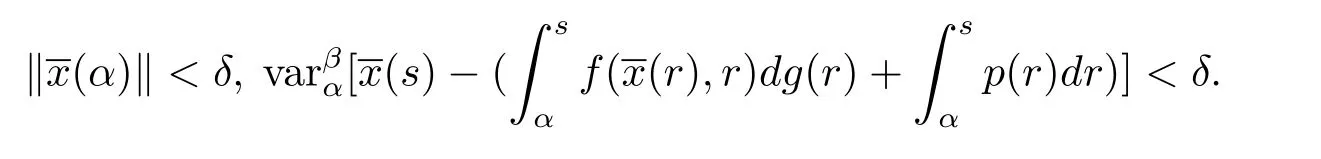
因此由(3.7)和(3.8)式,有
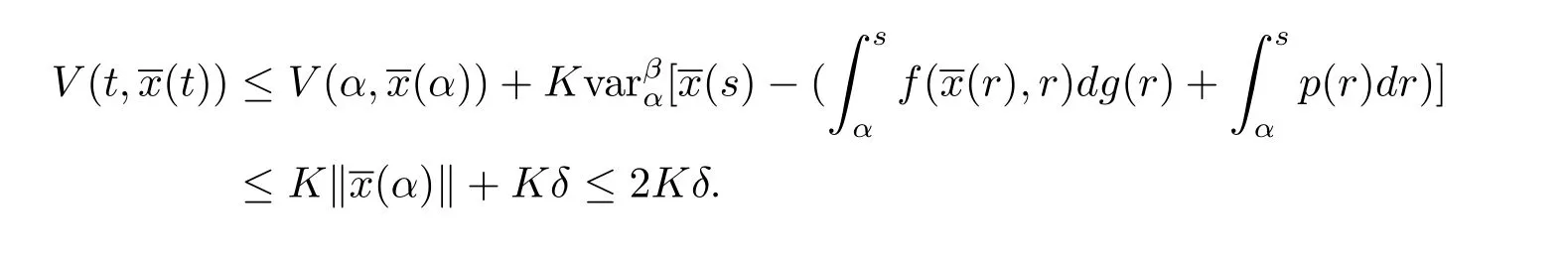
由于2Kδ<b(ε),则有
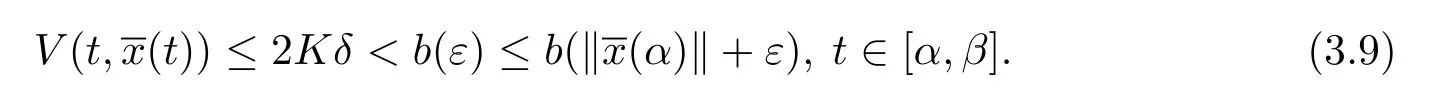
另外,由条件(iv),有
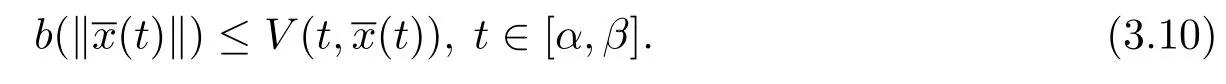
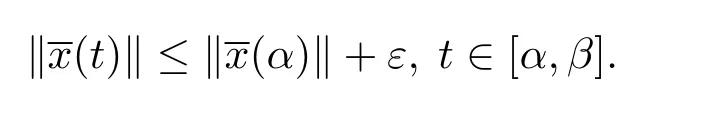
由定义3.3,取A=1,并且由ε的任意性,则满足,则测度微分方程(1.3)的平凡解x≡0是变差一致Lipschitz稳定的.
定理3.4设满足定理3.3中的条件(i),(ii),(iii)和(v),并且满足条件:
(iv′)对所有的有V(t,x)≥‖x‖.
则方程(1.3)的平凡解x≡0是一致整体Lipschitz稳定的.
证设是测度微分方程 (1.3)在 [α,β]上的解.由条件(iii),(v)及引理2.5和引理2.8,其中Φ≡0,所以对任意的t∈[α,β],有
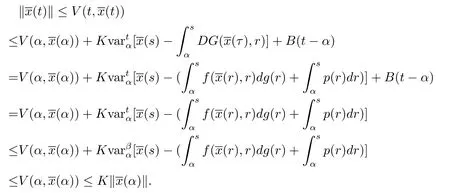
猜你喜欢
杂志排行
数学杂志的其它文章
- HYPOELLIPTIC ESTIMATE FOR SOME COMPLEX VECTOR FIELDS
- FAST AND SLOW DECAY SOLUTIONS FOR SUPERCRITICAL FRACTIONAL ELLIPTIC PROBLEMS IN EXTERIOR DOMAINS
- NORM STRUCTURES OF A FUZZY NORMED SPACE
- MODIFIED LAVRENTIEV REGULARIZATION METHOD FOR THE CAUCHY PROBLEM OFHELMHOLTZ-TYPE EQUATION
- BIFURCATION AND POSITIVE SOLUTIONS OF A p-LAPLACIAN PROBLEM
- 几类区域上不等维的边界唯一性定理
