FAST AND SLOW DECAY SOLUTIONS FOR SUPERCRITICAL FRACTIONAL ELLIPTIC PROBLEMS IN EXTERIOR DOMAINS
2020-09-21AOWeiweiLIUChaoWANGLiping
AO Wei-wei,LIU Chao,WANG Li-ping
(1.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)
(2.Department of Mathematics;Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice,East China Normal University,Shanghai 200241,China)
1 Introduction and Main Results
We construct classic solutions of the following supercritical nonlinear fractional exterior problem

wheres∈(0,1),andB1is the unit ball in RN.As usual,the operator(-Δ)sis the fractional Laplacian,defined at any pointx∈RNas

hereP.V.is a commonly used abbreviation for”in the principal value sense” andC(N,s)is a constant dependent ofNands.We refer to[6–7].
For classical Laplacian,namely,s=1,which is the Lame-Emden-Fowler equation

where Ω is a bounded open set with smooth boundary in RNandp>1 .Davila etc[4]proved(1.2)has in finitely many solutions with slow decayat infinity with eitherN≥4 andand Ω is symmetric with respect toNcoordinate axes.Later,this result was extended toand Ω is a smooth bounded domain by Davila etc[5].For fractional Laplacian,we will prove that this result also holds whens∈(0,1),andB1is the unit ball in RN.For problem(1.1)in general exterior domain,our method not be used to solve it,there exist some obstacles in Remark 1.
Our main results can be stated as follows:
Theorem 1.1For anys∈(0,1)and,there exists a continuum of solutionsuλ,λ>0 ,to problem(1.1)such that
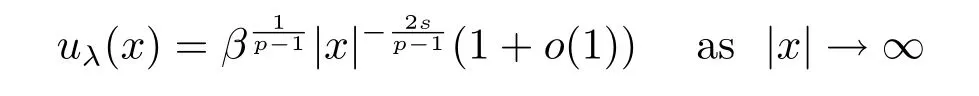
anduλ(x)→0 asλ→0 ,uniformly in.
Theorem 1.2For anys∈(0,1),there exists a number,such that for anyproblem(1.1)has a fast decay solutionup,up(x)=O(|x|2s-N)as|x|→+∞.
In order to prove Theorem 1.1,we will takeωas approximation of(1.1)whereωis a smooth,radially symmetric,entire solution of the following problem

hereβis a positive constant chosen so thatis a singular solution to(-Δ)sω-ωp=0 for which the existence and linear theory has been studied recently in[1]for the fractional case.
The basic idea in the proof of Theorem 1.2 is to consider as an initial approximation the functionλwhere

is the unique positive radial smooth solution of the problem

These scalings will constitute good approximations for smallλifpis sufficiently close toWe prove then adjusting bothξandλ,produces a solution as desired after addition of a lower order term.
By the change of variables

and the maximum principle(see the page 39 of[3]),problem(1.1)is equivalent to

whereλ>0 is a small parameter andB1λ,ξis the shrinking domain

Remark 1To prove Theorem 1.1 and Theorem 1.2,we will construct solutions of the equivalent problem(1.5)with the form=ω+φλ+φand=ω**+φλ+φ.To obtain the decay of,we need to know that the decay ofφλ+φ.Using the Poisson KernelP(x,y)inRNB1,we first obtain the decay ofφλis no more thanO(|x-ξ|2s-N).Secondly,we can derive the decay ofφby the Green functionG(x,y)inRNB1.But for general exterior domain,there is a lack of the explicit formulas and the decay of Poisson Kernel and Green’s function of fractional Laplace operator(-Δ)s.
The proof of Theorem 1.1 and Theorem 1.2 refers to[2]in detail.
