唐树安,冯小高

(1.贵州师范大学数学科学学院,贵州贵阳 550001)

(2.西华师范大学数学与信息学院,四川南充 637002)

1 引言

用Δ={z:|z|＜1}表示全平面C上的单位圆盘,用S1={z∈C:|z|=1}表示单位圆周.如果单位圆Δ内一个复值函数f满足

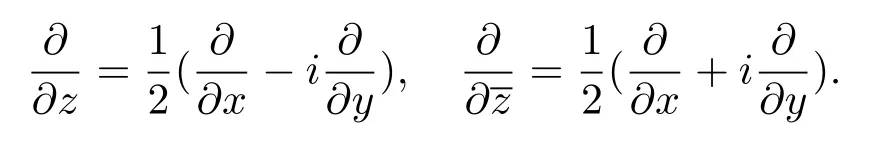
单位圆Δ内的调和映射f具有标准的分解f=h+,其中h和g在Δ内解析且g(0)=0.通过Lewy定理(见文献[1,2]),知道f是局部单叶的当且仅当f的雅可比行列式Jf=|h′|2-|g′|2在单位圆Δ内不为零.因此,如果f在单位圆内是局部单叶的,则或者Jf＞0,或者Jf＜0.如果雅可比行列式Jf＞0,称f是保向的;如果Jf＜0,则称其是反向的.对于一个保向的局部单叶调和映射f,是单位圆内的一个解析函数且|ωf|＜1,称之为f的第二复伸缩商.

设f是区域Ω上一个保向同胚,k是一个实数且0≤k＜1,如果f在Ω内的水平和垂直线上是绝对连续的,且满足下列方程

则称f是Ω内的一个k-拟共形映射,其中μ(z)被称为f复伸缩商且‖μ‖∞≤k＜1.0-拟共形映射是共形映射.f的第二复伸缩商定义为注意到|ωf|=|μf|,所以f是拟共形映射当且仅当|ωf|≤k＜1(见文献[3,4]).

设φ是Δ内的局部单叶解析函数,它的pre-Schwarian导数Pφ和Schwarian导数Sφ定义为

Nehari在文献[5]中证明如果Δ内的局部单叶解析函数φ满足

则φ在Δ内单叶.后来,Ahlfors和Weil在文献[6]中将这一结果推广,他们证明如果局部单叶解析函数φ满足

这里0≤t＜1,则φ在Δ内单叶且可以t-拟共形延拓至全平面C.

利用pre-Schwarzian导数,Becker在文献[7]中证明如果单位圆内的局部单叶解析函数φ满足

那么φ在Δ内单叶且可以拟共形延拓至整个复平面C.Ahlfors在文献[8]中具体构造这样一个拟共形映射.

设f是单位圆Δ内一个局部单叶调和映射,具有标准分解f=h+,它的pre-Schwarzian导数定义为

这里ω是f的第二复伸缩商.它的Schwarzian导数定义为

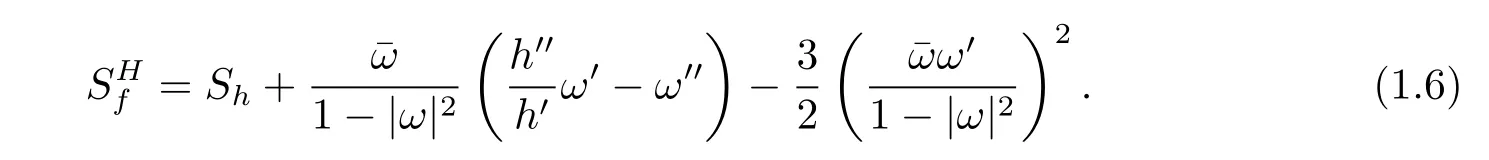
见文献[11].容易看出,如果f是解析函数,则ω=0,所以的定义与(1.1)的定义是一致的(见文献[11]).

定理 HM1(见文献[9])设f=h+是单位圆内的一个保向局部单叶调和映射且‖ω‖∞＜1.如果对所有的z∈Δ,

其中k满足

则f在Δ内单叶且可以拟共形延拓至整个复平面C.

借助于f的Schwarzian导数,他们在文献[10]中也得到如下结果.

定理HM2(见文献[10])设f=h+是单位圆内的一个保向局部单叶调和映射且‖ω‖∞＜1.则存在常数δ0＞0,使得若对所有的z∈Δ,

则f是单叶的并且可以拟共形延拓至整个复平面C,这里0≤t＜1.

定理G(见文献[12])设2≤p,φ是单位圆Δ到拟圆Ω的共形映射.则下列陈述等价

A3共形映射φ可以拟共形延拓至整个复平面C使得它的复伸缩商μ满足

这里指出,当p=2时,所对应的Teichmüller空间由崔贵珍在文献[13]中引进,这一空间被称为Weil-Petersson Teichmüller空间,它在数学和物理中都有重要应用.关于可积Teichmüller空间的更多结果,请参见文献[14–17].

自然的问题是,对于调和映射,是否也有对应于定理G的结果？在文献[18]中,作者证明了以下定理.

定理TF设f=h+是单位圆内的一个保向局部单叶调和映射,满足(1.7)式,其中k满足(1.8)式,且

1.2.1检查方法 使用GE Discover GSI 64排螺旋CT，扫描参数120kV，30mA，层厚5mm螺旋扫描，扫描时间5s左右，重建肺窗层厚为0.63mm、1.25mm。

如果

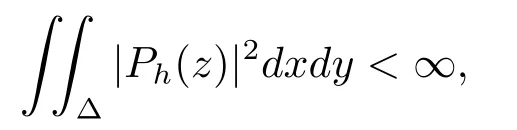
则调和映射f在单位圆内单叶且可以拟共形延拓至整个复平面C使得它的复伸缩商μ满足

本文进一步研究这一问题,主要结果如下

定理1设2≤p,f=h+是单位圆内的一个保向局部单叶调和映射,满足(1.7)式,其中k满足(1.8)式,且

则下列陈述等价

此外,如果条件B1或者B2满足,则调和映射f在单位圆内单叶且可以拟共形延拓至整个复平面C使得它的复伸缩商μ满足

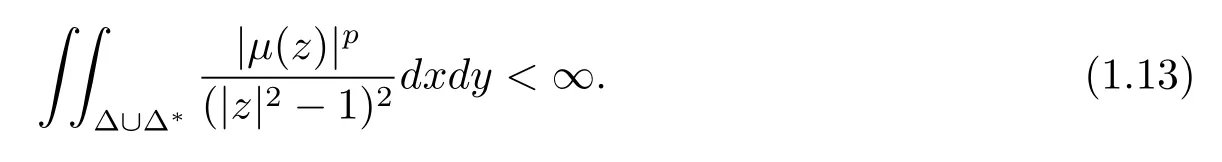
不知道定理1的第二个论断的反向是否成立.由定理G知道,当f是共形映射时,反向是成立的.

2 定理1的证明

本节将证明定理1.

首先证明B1⇔B2.因为f=h+是单位圆内的一个保向局部单叶调和映射,满足(1.7)式,其中k满足(1.8)式,由文献[9]中的定理2可知f可以单叶的延拓至={z∈C:|z|≤1},记其为f*,并且函数h是共形映射.所以由共形映射理论,有

(见文献[2,19]).根据调和映射的Schwarzian导数的定义,有

因为f满足(1.7)式,所以

其中k满足(1.8)式.于是由(2.2)式和(2.3)式,推出

注意到ω是单位圆Δ到自身的解析映射,由文献[20]中的结果可知存在常数C＞0,使得

由此可以推出

注意到‖ω‖∞＜1,由(2.3)式也可以推出

所以如果S 2成立,则由(1.1 2),(2.2),(2.4),(2.6)以及(2.7)式,可以推出

又因为h是共形映射,由定理G,知道(2.8)式等价于

根据pre-Schwarzian导数的定义可知

由(2.9)和(1.12)式,推出

反之,假定S1成立.由定义得到

由(1.12),(2.11)和(2.3)式,推出(2.9)式成立.又根据定理G,有(2.8)式成立.所以再次由f的Schwarzian导数的定义,得到

于是由(2.4),(2.6),(2.7)和(2.8)式,得到

因此完成了S1⇔S2的证明.

接下来证明定理1的第二部分.不妨假定S1成立.则由文献[9]的定理2,知道f在Δ内单叶且可以由下列公式拟共形延拓至整个复平面

其中

现在证明拟共形映射F的复伸缩商μF满足要求.事实上,如果|w|＜1,则有|μF(w)|=|ω(w)|.所以由条件(1.12),得到

现在假定|w|＞1,令.通过直接的计算,得到

所以有

通过直接的计算,也得到

注意到‖ω‖∞＜1,推出

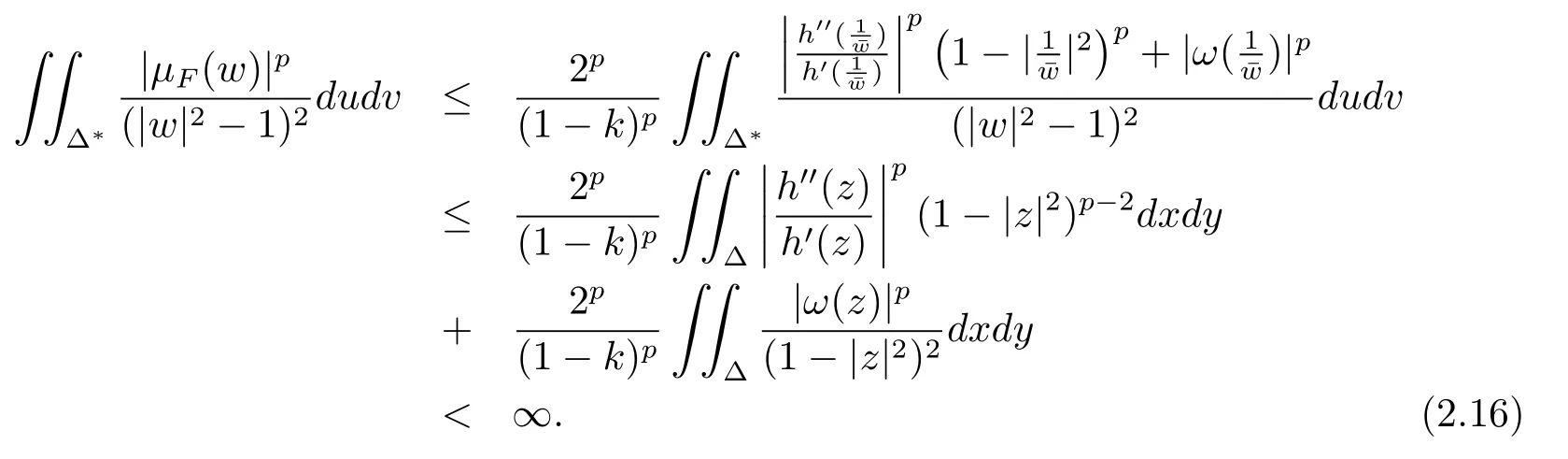
定理1证毕.