路紫薇，左可正，蒋万林

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

0 引言

用C表示复数域，用Cm×n表示复数域C上所有矩阵组成m×n的集合，In表示n阶单位矩阵.用A*,rank(A)，R(A)分别表示矩阵A的共轭转置、秩和值域空间.设A∈Cn×n，用ind(A)表示A的指数，即ind(A)=k是满足rank(Ak)=rank(Ak+1)的最小非负整数.

首先介绍需要用到的几种广义逆.

1)对矩阵A∈Cm×n,A的Moore-Penrose逆A+∈Cm×n是满足以下4个Penrose方程的唯一解[1-2]：

(1)

PA=AA+，QA=A+A分别是在R(A)，R(A*)上的正交投影算子.

2)设A∈Cn×n，ind(A)=k，则A的Drazin逆AD是满足下列3个矩阵方程的唯一解[3]：

(2)

特别地，当矩阵A的指数ind(A)≤1时，A的Drazin逆AD就是A的群逆A#，即A的群逆A#满足：

(3)

AA〇#=PA，R(A〇#)⊆R(A)

(4)

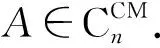
近年来，一些学者给出了core-逆的几种推广. 如2014年Prasad和Mohana在文献[5]中给出了core-EP逆A⊕的定义：

(5)

其中，k=ind(A).

(6)

(7)

(8)

其中,k(≥2)是正整数.

1 预备引理

为了得到主要的结果，需要下面一些已知的引理.

引理1[8](酉-上三角分解，QR分解)若A∈Cn×n且A可逆，则存在酉矩阵U及上三角矩阵T使得A=UT，且这种分解是唯一的.

引理2[9](核-幂零分解)设A∈Cn×n，ind(A)=k，则存在可逆阵P∈Cn×n，使得：

(9)

其中，G可逆；N为幂零矩阵，且Nk=0.

特别地，当rank(A)=rank(A2)=r时,有:

(10)

其中，G∈Cr×r，G可逆.

文献[10]中定理4.2给出了在引理2核-幂零分解下，矩阵A的Drazin逆AD的表达式为：

(11)

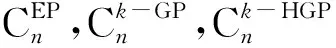
引理3[4]若A∈Cn×n，rank(A)=rank

(A2)=r，则A〇#=A#AA+.

引理4[11]若A∈Cn×n，ind(A)=k，则

A⊕=(Ak+1(Ak)+)+=(APAk)+.

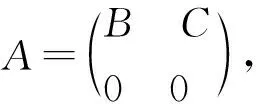
其中，R=BB*+CC*.

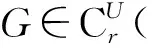
(12)

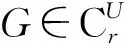
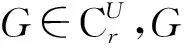
2 主要结果及证明

本文利用矩阵的酉-上三角分解和核-幂零分解，得到A的一些广义逆的核-幂零表达式.

若对式(10)中的可逆阵P进行酉-上三角分解，且对矩阵T进行相应的分块，令：

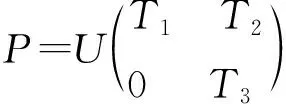
(13)

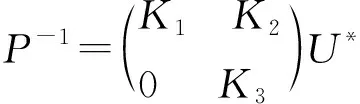
(14)

其中，T1，K1∈Cr×r；T2，K2∈Cr×(n-r)；T3，K3∈C(n-r)×(n-r)；U为n阶酉矩阵.

由PP-1=I,可得:

(15)

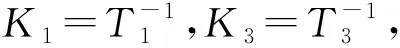
由式(15)有:

(16)

(17)

下面先给出在核-幂零分解下A+的表达式.

定理1 若A∈Cn×n，A≠0且rank(A)=rank(A2)=r，则：

(18)

其中，G∈Cr×r；T1,T2,T3,K1,K2,K3由式(10)和式(14)给出,且：

(19)

证明由已知条件及核-幂零分解引理知存在可逆阵P∈Cn×n，使得：

(20)

利用式(16)有：

(21)

其中，G∈Cr×r；T1,T2,T3,K1,K2,K3由式(10)和式(14)给出.

根据引理5可知：

(22)

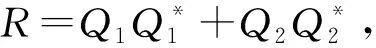
(23)

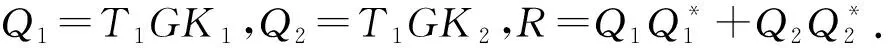
从而：

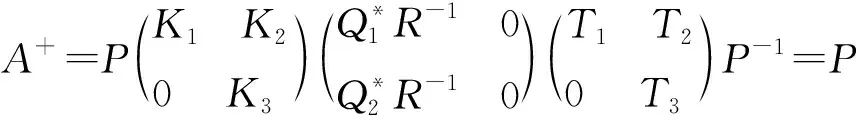
(24)

定理2 若A∈Cn×n，A≠0且rank(A)=rank(A2)=r,则：

(25)

(26)

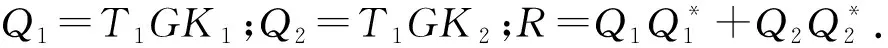
证明由定理1,利用式(10)和式(18)直接计算可得：

PA=AA+=

(27)

QA=A+A=

(28)

定理3 若A∈Cn×n，A≠0且rank(A)=rank(A2)=r,则:

(29)

其中，G∈Cr×r；T1,T2由式(10)和式(14)给出.

证明由引理3可知A〇#=A#AA+，所以：

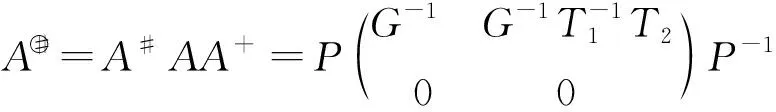
(30)

以上所给的是core-逆A〇#的核-幂零形式的表达式，当然也可以用酉相似来刻画，core-逆A〇#用酉相似表示如下：

(31)

定理4 若A∈Cn×n，A≠0，ind(A)=k，rank(A)=r，则：

(32)

其中，G∈Cr×r；T1,T2由式(14)给出.

证明因为A∈Cn×n，且ind(A)=k，由核-幂零分解可得,存在可逆阵P∈Cn×n，使得：

(33)

其中，G可逆；N为幂零矩阵，且Nk=0.

(34)

(35)

此时，由引理5可知：

(36)

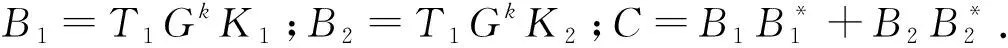
故：

Ak+1(Ak)+=

(37)

因此,由引理4有：

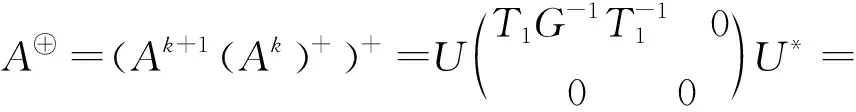
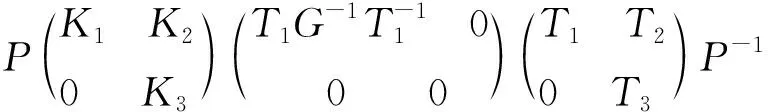
(38)

3 应用

利用由矩阵的核-幂零分解得到的Moore-Pensore广义逆A+，core-逆A〇#，PA=AA+，QA=A+A，A⊕的核-幂零表达式，来研究EP阵，k-广义投影算子和k-超广义投影算子的特征.

定理5 设A∈Cn×n，A≠0，rank(A)=r，ind(A)=1,且有式(10)和式(16)的表达式，则：

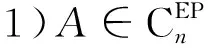
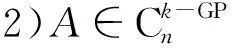
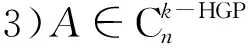
证明

1)根据定理2可知：

(39)

(40)

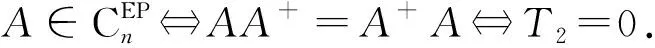
2)根据式(16)式可知:

(41)

(42)

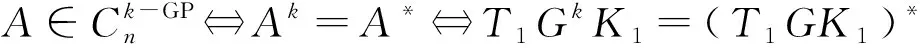
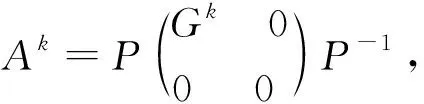
(43)

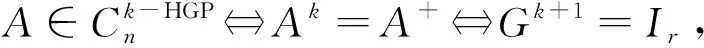
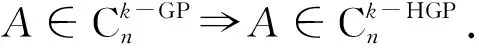
定理6 设A∈Cn×n，A≠0，则下列各命题彼此等价：

(b)A+=A〇#;

(c)A+=AA+A〇#;

(d)A+=A〇#AA+;

(e)A+=AA〇#A#;

(f)A〇#A#=A#A〇#;

(g)A#A#A〇#=A#A〇#A#;

(h)A#A#A〇#=A〇#A#A#;

(i)A〇#A〇#A#=A〇#A#A〇#;

(j)A〇#A〇#A#=A#A〇#A〇#.

证明仅证明(a)⟹(b)，(b)⟹(c)，(e)⟹(f)，(j)⟹(a)，其余的类似可证.

(b)⟹(c) 根据式(17)和式(28)可知：

(44)

(45)

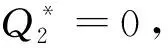
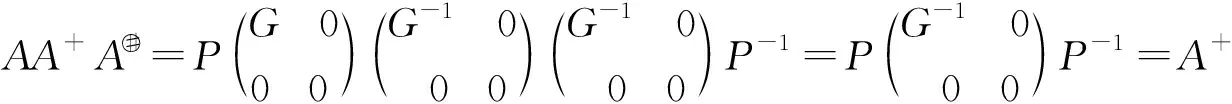
(46)

(e)⟹(f) 根据式(17)，(18)，(22)和(46)可知：

(47)

(48)

因为A+=AA〇#A#，注意到，Q2=0⟺T2=0，那么T2=0，从而：

(49)

(j)⟹(a) 根据式(17)和式(29)可知:

(50)

(51)

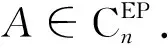
定理7 设A∈Cn×n，A≠0，则下列各命题彼此等价：

(b)A*=(A〇#)k+2；

(c)(A#)k+2A#AA*；

(d)(A〇#)k+2=AA*A#;

(e)(A〇#)k+2=A*AA〇#;

(f)(A#)k+2=A*AA〇#;

(g)(A#)k+2=AA*A〇#;

(h)A*=Ak+1A〇#;

(i)A*=A#Ak+1.

证明仅证明(a)⟹(b)，(g)⟹(h)，(i)⟹(a)，其余的类似可证.

(52)

其中，T1GkK1=(T1GK1).

根据引理6可得出T1Gk+1K1=Ir，Gk+1=Ir，从而：

(53)

(g)⟹(h) 根据式(16)，式(17)和式(31)可得：

AA*A〇#=

(54)

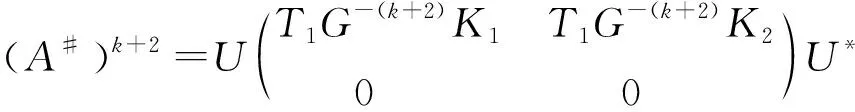
(55)

因为(A#)k+2=AA*A〇#，那么K2=0且T1G-(k+2)K1=(T1GK1)*，故T2=0且T1G-(k+2)K1=(T1GK1)*，由引理6可知T2=0且T1G-(k+2)K1=(T1GK1)*⟺T2=0且T1GkK1=(T1GK1)*，从而：

(56)

定理8 设A∈Cn×n，A≠0，则下列各命题彼此等价：

(b)A+=(A〇#)k+2;

(c)(A#)k+2=A#PA;

(d)(A〇#)k+2=PAA#;

(e)(A〇#)k+2=A+AA〇#;

(f)(A#)k+2=A+AA〇#;

(g)(A#)k+2=PAA〇#;

(h)A+=Ak+1A〇#;

(i)A+=A#Ak+1.

证明仅证明(a)⟹(b)，(f)⟹(g)，(i)⟹(a)，其余的类似可证.

(57)

(f)⟹(g) 对式(11)，式(25)和式(28)进行计算可知：

(58)

(59)

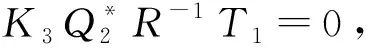
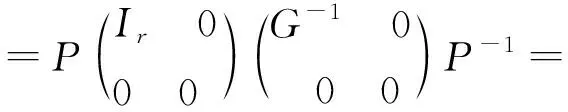
(60)

(i)⟹(a) 由于：