王文荣 解永晓

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

随着中国经济社会的快速发展，人流量与车流量与日俱增，产生了很多交通问题.交通事故的发生造成了很大的财产损失和人员伤亡，并且财产损失和人员伤亡的数额与交通事故发生的数目成正比.因此，道路交通事故也成为越来越值得关注和研究的问题，我们应该全面掌握数据自身所具有的特征以及呈现出的发展规律，对未来的交通事故数据进行预测，以便做好相应地防范措施.

许多有关交通问题的研究，都采用ARIMA模型，该模型应用非常广泛.Contreras(2003)[1]、Cuaresma(2004)[2]和Conejo(2005)等人[3]针对电价这一相关问题的研究均建立了ARIMA模型，并进行预测.2009年，李春燕[4]通过建立ARIMA模型来对交通事故死亡率进行分析预测，并且对交通事故的影响因素进行分析.道路交通系统是一个动态的时变系统，影响交通安全的许多因素都是灰色的，2015年，Xie[5]用灰色系统理论对交通事故问题进行研究，对事故起数、死亡人数、受伤人数、直接经济损失的数据进行了预测.采取灰色理论比较符合道路安全的客观状况，但是当数据变化幅度过大时，灰色模型会出现吻合程度差、精度较低的问题.2018年，Xie[6]通过建立ARMA模型对交通事故的死亡人数来进行分析.Duffie(1999)[7]、Escribano(2002)[8]、Longstaff和Wang(2004)[9]、Hadsell和Shawky(2006)[10]、Hadsell(2004)[11]、Knittel(2005)[12]在研究电价问题时均考虑了方差非齐性的影响，在ARIMA模型的基础上建立了条件异方差模型，对数据进行了波动性分析以及对称性分析.我们对Xie[6]的论文中残差序列进行异方差检验，发现其残差序列的方差也是非齐的，但其文章并没有提及异方差问题.

本文以1990-2017年的交通事故数据为样本，建立关于交通事故的时间序列，并通过数据的预处理和模型的识别、检验与优化提取序列的相关信息，建立了ARIMA模型.在此基础上考虑异方差的影响，通过对模型的残差序列进行异方差检验，发现序列之间方差非齐性，建立了条件异方差模型-EGARCH模型，并根据所建立的模型对交通事故序列进行预测.以2017年的数据来检验预测精度，并将预测得到的未来几年交通事故的结果进行比较，验证了ARIMA-EGARCH模型的预测精度更高，预测误差更小.

2 模型介绍

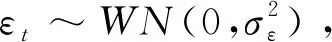
Φ(B)dxt=φ0+Θ(B)εt

(1)

称为ARIMA(p,d,q)模型，其中，d为差分阶数，p为自回归系数多项式Φ(B)=1-φ1B-…-φpBp的阶数，q为移动平均系数多项式Θ(B)=1-θ1B-…-θqBq的阶数.

2.2GARCH模型1985年，Bollerslov提出了广义自回归条件异方差(GARCH (p,q))模型，它的结构如下：

(2)

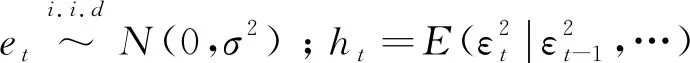
2.3EGARCH模型EGARCH模型又称为指数GARCH模型，由Nelson在1991年提出. EGARCH(p,q)模型的条件方差表达式为

(3)

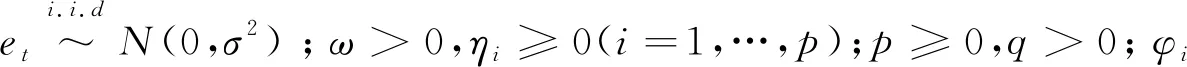
3 模型建立

3.1数据的预处理数据的预处理包括平稳性检验和纯随机性检验.可以通过观察值序列时序图的波动变化来判断序列的平稳性，或者对序列进行单位根检验.本文显著性水平α均取0.05.

图1是1990-2017年中国交通事故数据{xt}的时序图，从图中可以看出,1990-2017年中国交通事故的数据序列不是在一个常数值附近随机波动，该序列在1998-2008年附近有显著的变化趋势，即该序列有明显的趋势性，可判断此序列是不平稳的,需要对{xt}进行一阶差分.对于差分后的序列{st}进行平稳性检验.通过差分序列的ADF检验得到检验的P值为0.005 4，明显小于显著性水平，故差分后的序列{st}是平稳的.

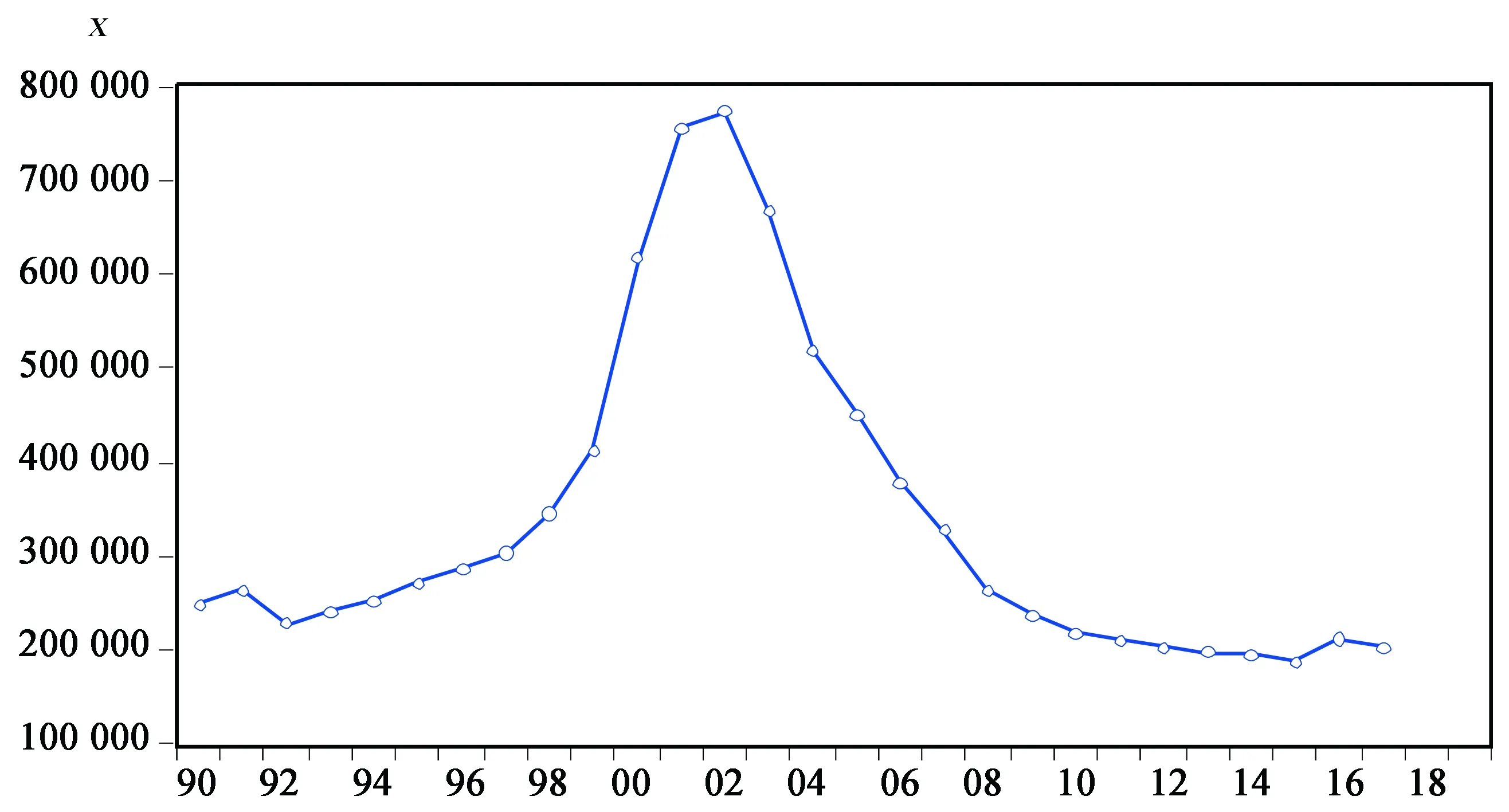
图1 1990-2011年中国交通事故数据{xt}时序图

下面对差分序列{st}进行纯随机性检验,图2为差分序列的自相关图.由图中检验的P值均小于α可知差分序列不是纯随机序列，即序列值之间存在相关关系.

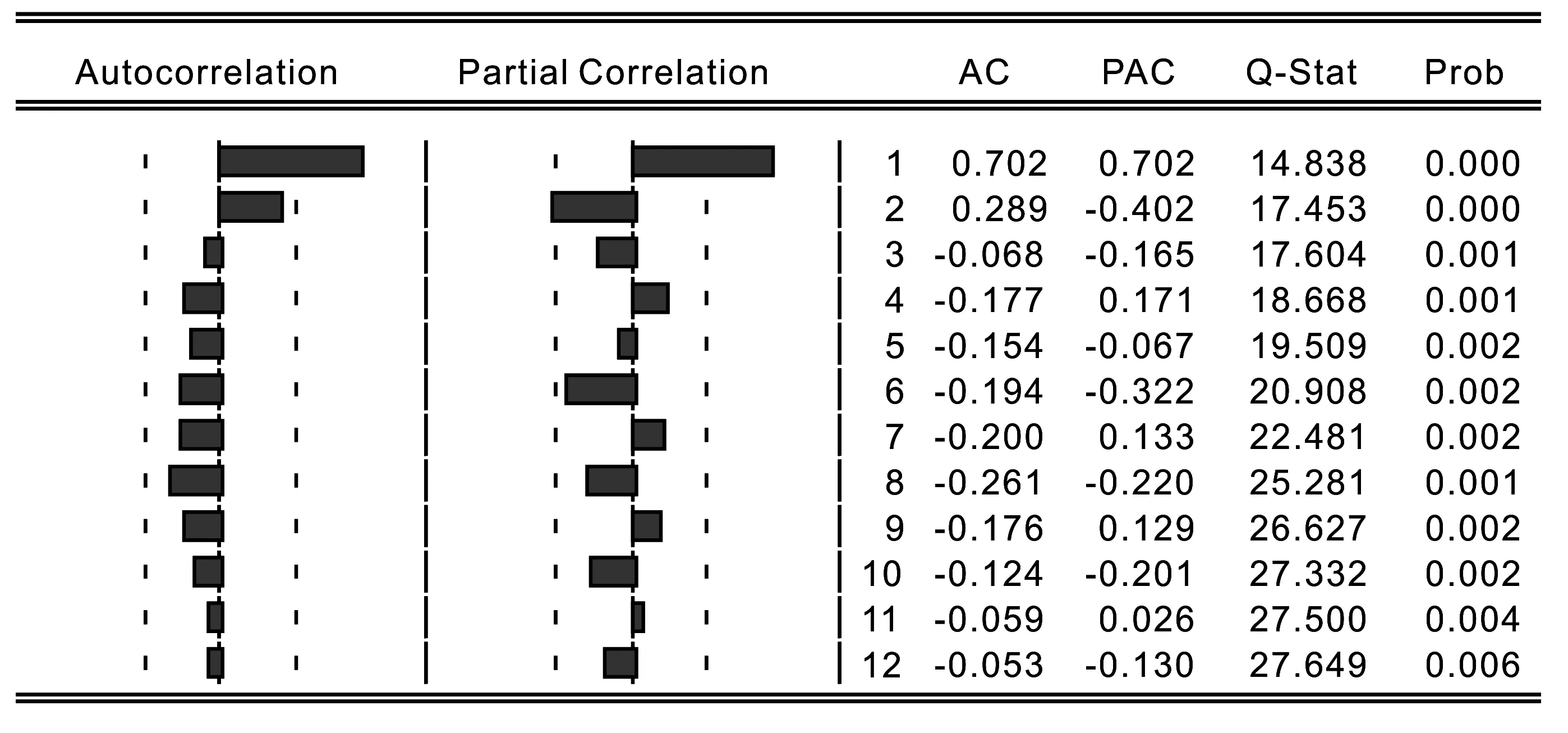
图2 差分序列{st}的自相关图

3.2模型识别与参数估计将1990-2017年中国交通事故的数据经过预处理之后，得到平稳、非纯随机的序列{st}，用ARMA(p,q)模型进行拟合.模型的识别就是确定模型ARMA(p,q)中的阶数p、q，本文采用最小信息量(AIC)准则选出最优模型进行拟合.

由表1可以看出，最优化的拟合模型为ARIMA(2,1,2).

表1 最小信息量表

下面对模型的参数进行估计，结果如表2所示.

表2 ARIMA(2,1,2)模型拟合结果

通过观察检验结果中的P值可以看出，φ1,φ2与θ2所对应的P值远大于显著水平α的值，因此，该模型不是序列的有效拟合模型.考虑ARIMA(0,1,1)模型，进一步对模型进行参数的估计与检验，结果如表3所示.可以看出，检验的P值小于α的取值，从而模型中的参数都是显著非零的.

表3 ARIMA(0,1,1)模型拟合结果

但是，通过表1可以看出，MA(4)的AIC值为23.950 24，小于MA(1)的AIC值24.397 07.因此，考虑拟合模型ARIMA(0,1,4)，结果如表4所示.

表4 ARIMA(0,1,4)模型拟合结果

由上图可以看出，参数θ3所对应的P值远远大于显著性水平α，说明参数θ3不显著.因此去掉该参数，对模型进行重新拟合分析，拟合结果如表5所示，并且此时对应的AIC值最小，说明该模型为最优化的模型.

表5 ARIMA(0,1,4)模型重新拟合结果

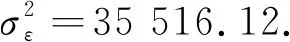
(4)

3.3条件异方差模型已知原序列{xt}拟合的模型为ARIMA(0,1,4),图3为残差平方序列{rt}的时序图，可以看出残差平方序列具有显著的差异性，因此得出残差序列的方差是非齐性的.

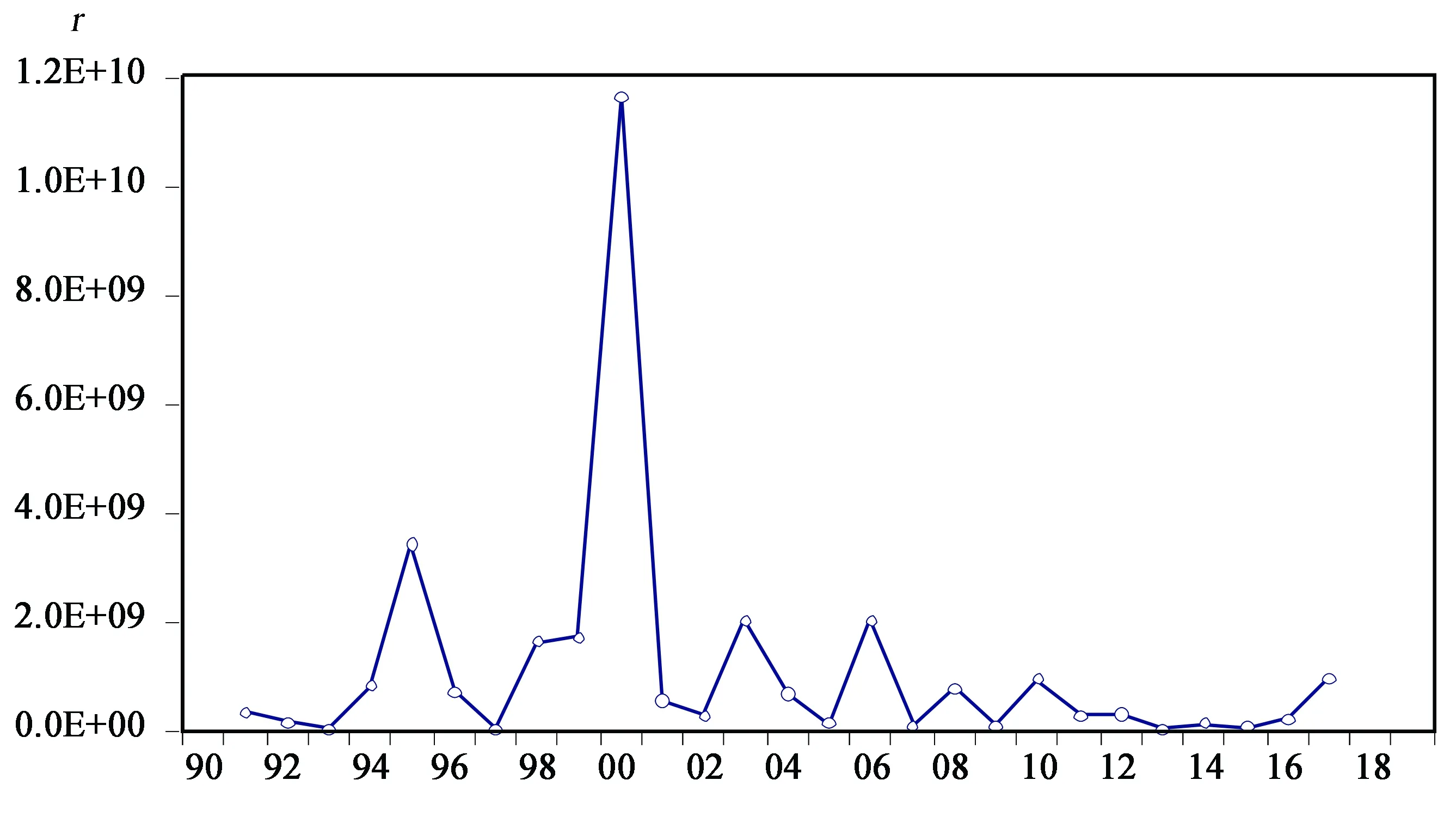
图3 残差平方图

对模型的残差序列{εt}进行异方差检验，通过检验得到检验的P值明显小于显著性水平α，所以可认为残差平方序列{rt}具有显著自相关关系，残差序列{εt}具有异方差性.

对于残差序列{εt}的异方差性，我们建立条件异方差模型来消除异方差性，最常用的两种条件异方差模型为ARCH模型和GARCH模型.其中ARCH模型只适用于残差平方序列具有短期自相关的情况，而GARCH模型考虑残差平方序列具有长期自相关的情况.GARCH模型是应用范围非常广泛的一种异方差序列拟合模型，但它对参数的约束非常严格，要求模型的参数都是非负的，这在一定程度上限制了GARCH模型的适用范围.为了消除这一约束，我们考虑用EGARCH模型来拟合，结果如表6所示.

表6 EGARCH模型拟合

其中，C(2)、C(3)、C(4)和C(5)分别代表上式(3)中的参数ω、α、φ和η的估计值.由表6可以看出，参数ω和η所对应的P值均大于显著性水平α的取值，说明这两个参数不是显著非零的；参数α和φ所对应的P值均较小，参数显著非零.并且由表6可以得到参数的估计值分别为：α=-2.428 107，φ=2.397 456.此时模型表达式为

(5)

因此，我们最终得到的模型为

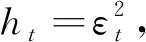
(6)

4 模型预测

通过以上建立的ARIMA(0,1,4)-EGARCH(1,1)模型来对残差平方序列进行预测，预测结果如图4所示.

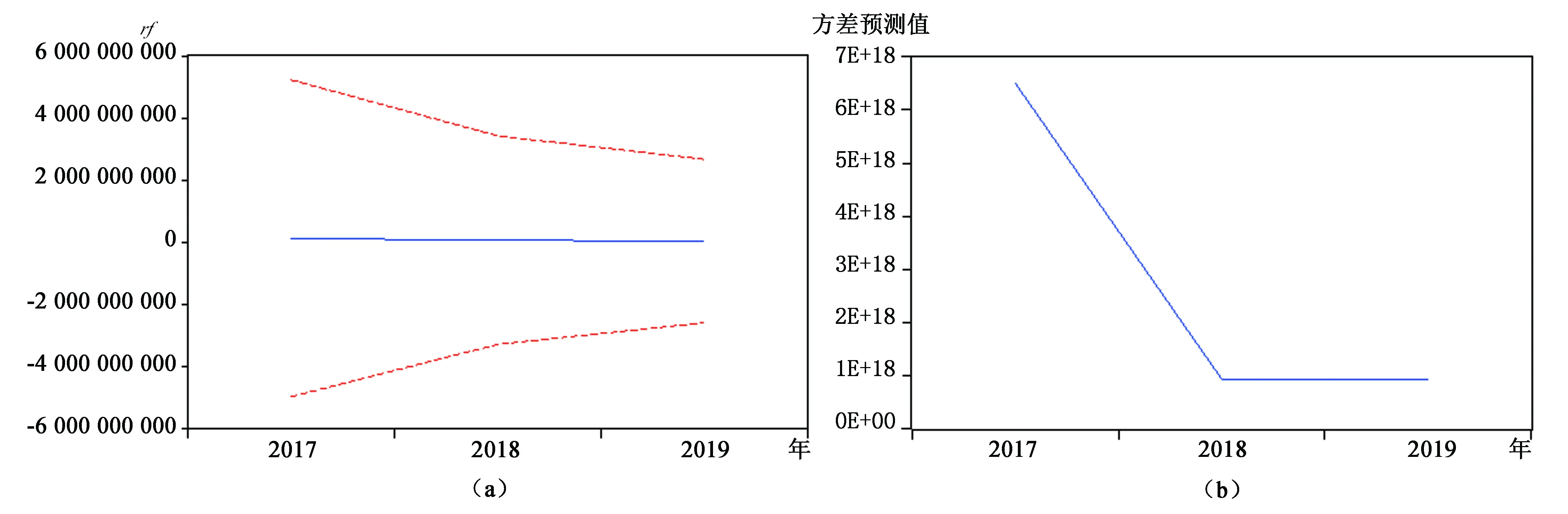
图4 ARIMA(0,1,4)-EGARCH(1,1)预测效果图

上图中rf为残差平方的预测值，两条虚线表示的是残差平方序列预测值的95%的置信区间.从图中可以看出，方差的预测值呈现出减小的趋势，最终预测值在零值附近，收敛到无条件方差.

对2017年的交通事故发生起数进行预测，并将两模型的预测值与实际值进行对比，如表7所示，从表中可以看出，ARIMA-EGARCH模型的预测精度大于ARIMA模型的预测精度，所以ARIMA-EGARCH模型的预测精度较高，可以进一步对2018和2019年的交通事故发生起数进行预测，预测结果分别为：198 194,194 172.

表7 两模型实际值与预测值的比较

运用ARIMA模型与ARIMA-EGARCH模型分别对2013-2017年的交通事故起数进行预测，表8为模型的预测效果对比，通过对比均方误差、平均绝对误差以及平均绝对百分比误差来评估两个模型的预测精度，误差值越小，预测精度越高.由表8看出，ARIMA模型的误差值大于ARIMA-EGARCH模型，故ARIMA-EGARCH模型的预测性能优于ARIMA模型.

表8 模型预测效果对比