张 翊 王秀丽

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

现代统计实践中，模型选择的问题已经得到了广泛的关注，为了选择最优模型，许多学者已经提出了大量的准则，例如AIC,BIC和FIC准则.然而，提前给定模型，往往忽略了额外的不确定性，从而可能低估了标准误差，因此对多个模型进行加权估计，而不依赖于单个模型的模型平均受到了广泛的关注，例如：文献[1]考虑了线性模型的FIC模型平均方法，文献[2]和[3]将FIC模型平均扩展到了一系列非参模型，文献[4]研究了模型平均估计的置信区间，文献[5]对可加部分线性模型(APLM)的模型平均进行了研究.数据缺失也是在处理数据时经常遇到的问题，文献[6]提出了缺失数据下变系数部分线性模型的模型平均，文献[7]利用借补的思想研究了线性模型缺失响应变量下的模型平均.本文参考了文献[5]利用扩张的逆概率加权方法填补数据的思想，考虑了线性模型在响应变量缺失下的模型选择和模型平均.因此本文在假设响应变量Y是随机缺失(MAR)的前提下，利用聚焦信息准则(FIC)和频率模型平均(FMA)对线性模型的模型平均进行了研究，其中对于缺失数据的填补利用了扩张的逆概率加权(AIPW)方法.

2 模型框架和估计过程

本文考虑如下的线性模型

Y=XTβ+ε，

(1)

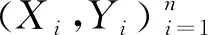
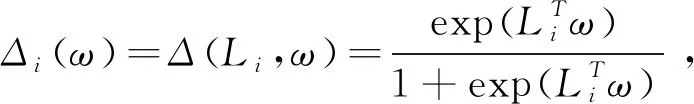
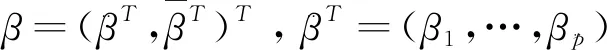
(2)

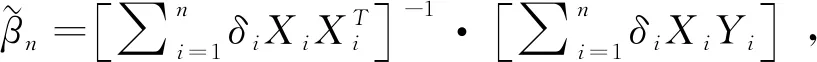
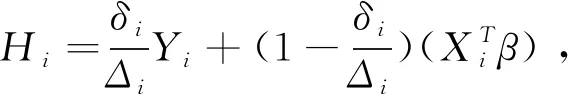
(3)

定理1在条件(H1)-(H3)成立以及满足局部误设框架的情况下，

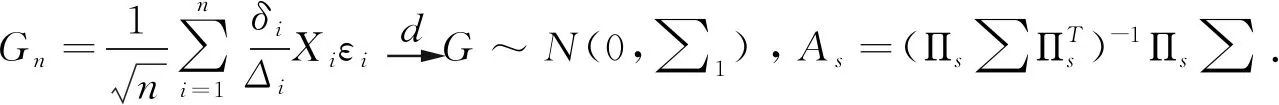
3 FIC和模型平均

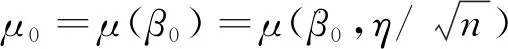
定理2在满足局部误设框架及条件(H1)-(H3)的前提下，

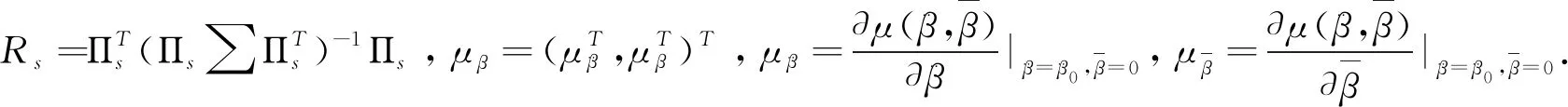
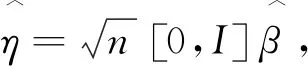
(4)

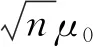
定理3在满足局部误设框架及条件(H1)-(H3)的前提下，并且权函数连续，有

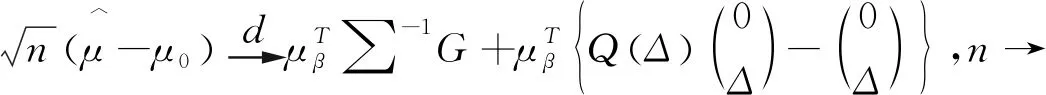
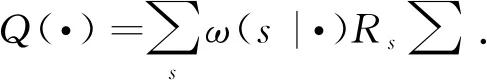
4 条件及主要证明

4.1 假设条件

H1 对于任意的L′s，Δ(L,ω)是关于ω已知的可微函数.

H2Δ(·)关于ω二次可微，并且存在正数C0使得infΔ(·)≥C0>0.

H3 矩阵∑，∑0以及∑1是可逆的.

4.2 主要证明

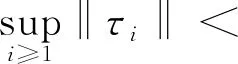
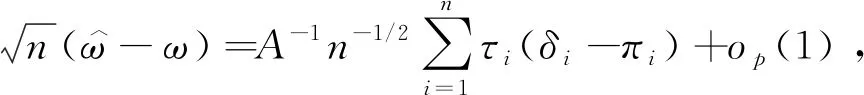
引理2[11-12]在局部误设框架和条件(H1)-(H3)下，

(5)

其中

因此，由上面的引理1，得

由条件(H1)-(H3)，有

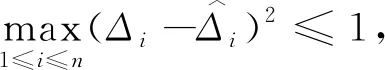
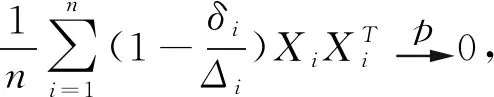
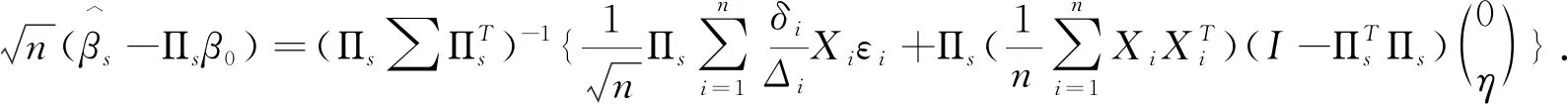
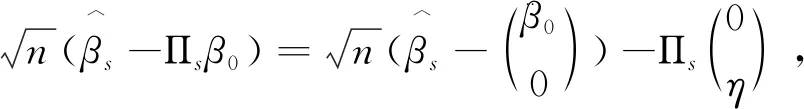
然后证明定理2.类似文献[6]的证明，由泰勒展开式知:

因此，由定理1可以推出：