带有分数阶Laplace算子的偏微分方程解的存在性研究进展
2020-07-23刘衍胜
刘衍胜 王 洋
( 1) 山东师范大学数学与统计学院,250358, 济南; 2) 山东管理学院信息工程学院, 250357, 济南 )
1 引 言
偏微分方程是现代数学领域的一个重要分支,许多应用学科,例如物理学、化学、生物学、力学、农学、环境、医学,甚至经济学等社会科学领域大量出现的数学模型通常都可以归结为偏微分方程.作为偏微分方程理论的一个特殊分支,分数阶偏微分方程理论近年来广泛应用在流体力学、量子力学、电分析化学、粘弹性力学、生物系统的电传导、信号和图像处理、机器人控制、高分子材料的解链、混沌现象、分子光谱等领域,并逐渐成为科学研究的热点问题,具体可参见文献[1-5].与整数阶偏微分方程相比,分数阶偏微分方程不仅在刻画自然现象、描述生产和生活中的动态过程方面比整数阶偏微分方程更加精准和细致,而且可以避免整数阶偏微分方程模型与科学实验结果不吻合的弊端.
带有分数阶Laplace算子的偏微分方程是一类典型的分数阶偏微分方程,它在科学及工程领域有着重要的应用,如相变理论、液体中的化学反应、有记忆的随机游走、人口动力学、金融中的美式期权、极小曲面、优化问题等,详见参考文献[6-8].分数阶Laplace算子是经典Laplace算子的一种推广,继承了Laplace算子的一些重要性质,例如有界线性、自共轭性等,这为分数阶Laplace算子的研究提供了方便.然而,由于分数阶Laplace算子的非局部性和奇异性,使它与经典的Laplace算子有着本质的区别,从而导致一些经典性质的消失,这就给此类问题的研究带来了较大困难.因此,研究带有分数阶Laplace算子的偏微分方程是一项既具有现实意义又具有挑战性的工作.
一般来说,求解带有分数阶Laplace算子的偏微分方程的显式解并非易事,因此对其解的存在性研究是非常必要的.目前,关于此类方程解的存在性研究所使用的主要方法有不动点定理、拓扑度理论、上下解方法、变分方法和临界点理论等,其中变分方法和临界点理论是最常用的方法.变分方法的基本思想是把微分方程的求解问题归结为求方程所对应的能量泛函在一定条件下的极值问题或临界点问题,它内容丰富, 具体可参见文献[9-12].古典变分法的基本内容是确定泛函的极值和极值点来求解微分方程,它主要通过研究泛函的极小化序列并结合泛函的下半连续性来得到极小值点,这种方法被称为极小化理论,至今仍然是研究微分方程解的存在性的主要方法之一.但由于欧拉方程的解在一般情况下并不是其对应泛函的极值点,而是对应泛函的临界点,因此,极值问题的进一步发展就是临界点理论.它主要依靠的是拓扑工具,考虑构成整个变分问题的流形,从泛函本身的性态判定出未必是极值点的临界点.1973年,Ambrosetti和Rabinowitz[13]提出了山路引理,这是临界点理论发展史上的一个里程碑.随后,一系列的极大极小形式的新定理被建立起来,并成为研究具有变分结构的微分方程解的存在性和多重性的有效工具,具体可参见文献[14-19].
由于分数阶偏微分方程解的存在性成果众多,很难在一篇文章中全面阐述.因此,本文仅对熟悉的几类带有分数阶Laplace算子的偏微分方程解的存在性研究进展与动态进行阐述.在本文第二节,将简要回顾分数阶Laplace算子概念和几类带有分数阶Laplace算子的偏微分方程,第三节主要介绍带有分数阶Laplace算子的偏微分方程解的存在性研究进展,最后一节为研究展望.
2 分数阶Laplace算子与带有分数阶Laplace算子的偏微分方程
本节中,我们首先对分数阶Laplace算子和分数阶Sobolev空间的基础知识进行回顾,接下来介绍与本文相关的几类带有分数阶Laplace算子的偏微分方程的物理背景.
2.1分数阶Laplace算子相对于标准的局部微分算子-Δ来说,分数阶Laplace算子(-Δ)s是一类非局部的拟微分算子,它可以充分体现系统的历史依赖性,能精确描述反常力学行为路径和全局相关的特性.另外从概率的观点来看,分数阶Laplace算子(-Δ)s是Lévy稳态过程的无穷小生成元[20-22].在实际应用中,分数阶Laplace算子(-Δ)s以各种形式出现在各种模型中,如分数阶Schrödinger方程、分数阶Kirchhoff方程、分数阶期权定价模型、分数阶多孔介质方程、分数阶Navier-Stokes方程、分数阶Yamabe问题、分数阶Allen-Cahn方程、分数阶Cahn-Hilliard方程等.Laplace最早用积分的形式给出了(-Δ)s的定义,随后Fourier利用Fourier变换给出了(-Δ)s的定义,详见参考文献[23].
下面给出分数阶Laplace算子(-Δ)s的这两种定义. 记S表示RN中快速衰减的C函数构成的Schwartz空间,令s∈(0,1).
定义1假设u∈S,那么函数u的分数阶Laplace导数定义如下:
其中CN,s表示一个依赖于N和s的常数,P.V.代表Cauchy主值.
定义2假设u∈S,那么函数u的分数阶Laplace导数定义如下:
(-Δ)su(x)=F-1(|ξ|2sFu(ξ)),
其中Fu(ξ)表示函数u的Fourier变换.
2.2 分数阶Sobolev空间
定义3齐次分数阶Sobolev空间Ds,2(RN)定义如下:
其上的半范数定义为
可见如此定义的Ds,2(RN)在内积
下构成一个Hilbert空间.
定义4分数阶Sobolev空间Hs(RN)定义如下:
其上的半范数定义为
其内积定义为
可知,Hs(RN)为Hilbert空间.
2.3 带有分数阶Laplace算子的偏微分方程
2.3.1 分数阶Schrödinger方程 分数阶Schrödinger方程是分数阶量子力学的基本方程.由Laskin通过扩展Feyman路径积分,将Brown型量子力学路径扩展到Lévy型量子力学路径得到,最初形式如下:
其中,i 表示虚数单位,V表示位势函数,φ表示波函数,0 φ(x,t)=e-iωtu(x), 即研究下列方程: (-Δ)su+V(x)u=f(x,u),x∈RN. (1) 方程的驻波解可以描述光束中的孤立子、物体的热脉冲传播、超导电子在磁场中的运动和Bose-Einstein凝聚效应等现象.当s=1时,上述方程就变成了经典的Schrödinger方程,对此已有丰富的研究成果,详见参考文献[24-29]. 2.3.2 分数阶Schrödinger-Poisson方程 分数阶Schrödinger-Poisson方程最初形式如下: 该方程来源于量子力学模型,δ=1表示排斥,δ=-1表示吸引.一般主要考虑在静电场排斥的情况下,上述方程驻波解的存在性.即考虑如下方程 (2) 其中 因此,相比较研究分数阶Schrödinger方程,研究分数阶Schrödinger-Poisson方程解的存在性和多重性问题的难度将会增大. 当s=t=1时,上述方程(2)就变成了经典的Schrödinger-Poisson方程,对此已有丰富的研究成果,主要包括: 基态解的存在性、半经典解的存在性、多个高能量解和多个低能量解的存在性、定号解及变号解的存在性与多重性、解的不存在性等,详见参考文献[30-38]. 2.3.3 分数阶Kirchhoff方程 近年来, 如下形式的Kirchhoff方程 其中a>0,b≥0,一直受到人们的广泛关注.这是因为这类方程所涉及的大量问题来源于物理学、生物学、化学中的数学模型,如等离子体问题、非牛顿力学、弹性理论、天体物理学等.事实上,该方程与Kirchhoff在文献[39]中研究的关于弹性弦自由振动时提出的一个定态问题的模型 相关.在一定意义下, 它可以看作是如下经典Alembert波方程的推广 2014年,在文献[52]中,Fiscella和Valdinoci首次建立了含有分数阶Laplace算子的定态Kirchhoff 模型.随后,如下分数阶Kirchhoff方程 (3) 也引起了学者们的广泛关注. 由于方程(1),(2),(3)都是具有变分结构的分数阶偏微分方程,因此,都可以用变分方法来研究解的存在性.到目前为止,关于上述方程解的存在性,国内外学者获得了一些研究成果.在本小节中我们分别给出上述三类分数阶偏微分方程解的存在性研究进展. 3.1分数阶Schrödinger方程解的存在性对于分数阶Schrödinger方程,近年来引起许多学者的关注,他们利用变分法对方程(1)解的存在性和多重性做了大量的研究并得到了一系列的重要结果,具体可见参考文献[53-64].对该方程的研究大致分为两个方面:1) 权函数是恒正的或者是变号的;2) 非线性项是临界的或是次临界的.得到的结果包括正解、负解、基态解、半经典解、变号解的存在性和无穷多个解的存在性.运用的方法主要有:山路引理、对称山路引理、喷泉定理、变形的喷泉定理、环绕定理、Nehari流形、下降流不变集方法、集中紧定理等.如在文献[53]中,Felmer等利用山路引理得到了常值权函数的分数阶Schrödinger方程正解的存在性,并进一步分析了解的正则性,得到了与整数阶Schrödinger方程的解不同的衰减性质,最后利用移动平面法得到了解的对称性.在文献[54]中,作者利用拉格朗日数乘法证明了基态解的存在性,并用Nehari流形方法考虑了具有固定频率的束缚态解的存在性.在文献[55]中,作者利用变形的喷泉定理分别研究了非线性项在无穷远处满足渐进线性条件或超线性增长条件时,无穷多个高能量解或无穷多个低能量解的存在性.在文献[56]中,作者利用下降流不变集方法结合临界点定理,得到了正解、负解的存在性和变号解的存在性以及多重性. 3.2分数阶Schrödinger-Poisson方程解的存在性目前,对于分数阶Schrödinger-Poisson方程解的存在性和多重性,国内外学者取得了一些研究成果,包括正解、负解、基态解、半经典解、变号解的存在性和无穷多个解的存在性,详见参考文献[65-71].例如,在文献[66]中,当权函数V(x)是变号的,作者利用对称山路引理得到了无穷多个解的存在性.在文献[67]中,当权函数V(x)=1时,作者利用扰动方法和山路引理得到了非平凡解的存在性.文献[68]考虑临界情形下,利用Pohozaev-Nehari流形和集中紧定理得到了基态解的存在性.文献[69]利用形变引理,得到了至少一个低能量变号解的存在性. 3.3分数阶Kirchhoff方程解的存在性据我们所知,关于Kirchhoff方程解的存在性的结果并不是很多,仅见参考文献[72-75] 等.在文献[72] 中,作者利用Nehari流形方法得到了基态解的存在性.在文献[73] 中,作者利用单调迭代技术得到了基态解的存在性.在文献 [74] 中,作者建立了分数阶Kirchhoff方程的Pohozaev恒等式,得到了解的存在性和不存在性结果.文献 [75]利用下降流不变集结合山路引理,得到了正解、负解的存在性和变号解的存在性与多重性. 分数阶Laplace 算子是一类非局部奇异拟微分算子,它虽然保持了Laplace 算子的一些重要性质,如自共轭性、有界线性等,但是其非局部性和奇异性为相关问题的研究带来了实质性的困难.本文主要对几类带有分数阶Laplace 算子的偏微分方程解的存在性的研究动态和进展进行综述.就目前的研究现状来看,已经取得了一系列优秀的研究成果,但仍有一些问题值得更深入地探讨和研究. 1) 分数阶p-Laplace方程解的存在性研究.这个问题是将分数阶Laplace方程推广到分数阶p-Laplace方程.分数阶p-Laplace算子也是一类非局部算子,但是相比分数阶Laplace算子更加复杂,研究起来需要更多的分析技巧,难度将会增大. 2) 关于分数阶Laplace方程变号解的研究还有很大的空间.如解的变化的次数、结点域(解不等于零的连通分支)的现状等. 3) 关于分数阶Laplace 方程,大多数学者们只是对解的存在性和多重性进行了研究,但是关于解的性质的研究,如吸引性、稳定性等研究还不够系统和深入,这将是今后的一个重要研究方向.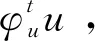
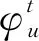
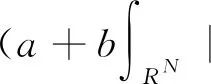
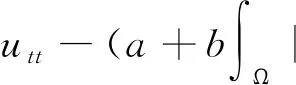
3 解的存在性研究进展
4 研究展望
