李茂青，刘建强，高锋阳，张廷荣

(兰州交通大学自动化与电气工程学院，甘肃兰州 730070)

1 引言

永磁同步电动机(permanent magnet synchronous motor，PMSM)具有结构简单、高效率、高气隙磁通密度和高功率因数等优点而被广泛地应用在国防、工业以及社会生活的各个领域，如航空装备、火炮、数控机床以及医疗等[1].因此，研究与改善交流PMSM伺服系统的控制策略具有重要的理论意义和实用价值.

PMSM为高阶、强耦合及非线性系统，传统的线性控制策略无法解决输入与输出的耦合以及输出的独立性控制等问题，无法满足高性能调速系统的控制要求.因此，国内外学者对非线性控制理论进行了广泛深入的研究，取得了一定的成果.应用到PMSM系统中的非线性控制理论主要有:滑模变结构控制[2-3]、反馈线性化[4]、反步法[5]、自抗扰技术[6]、及无源控制理论[7-8]等，这些非线性理论的应用极大的改进了系统的动静态性能.文献[3]提出了一种实时改进的滑模控制器，可实现整个伺服系统的稳态控制，但滑模控制多次的开关切换可能激活系统未建模的高频成分，从而导致系统失稳[9].文献[4]利用反馈线性化理论对PMSM进行全局线性化与解耦，并将线性化与解耦的电机模型写成可观测的Brunovski标准形，从而可有效地确定出系统的控制结构;缺点是所有的状态变量都必须精确测量，才可抵消非线性因素[10].文献[5]提出了一种改进的反步控制器，该控制器可提高速度的动态响应，实现良好的速度跟踪;缺点是无法对转子磁链进行有效的位置跟踪[10].文献[6]针对PMSM系统内部参数摄动和外界干扰的问题，运用自抗扰控制来对参数摄动和外界干扰进行观测和前馈补偿，实现了系统的线性化，提高了系统的抗干扰能力;缺点是参数的选取较多，与之对应的取值会影响系统控制性能[9].文献[7-8]将端口受控的哈密顿理论应用到PMSM系统中，利用互联和阻尼分配无源控制方法来设计系统控制器，提高了系统的动态响应，实现了全局的稳定;不足之处是没有实现位置控制.文献[11-12]通过在受控哈密顿系统中引入积分作用的动力学反馈、陀螺力和阻尼力，实现了一般哈密顿系统的鲁棒控制.若选择合适的陀螺力和阻尼力注入，则系统的动静态性能将会进一步提高.文献[13]将互联和阻尼配置的无源控制(interconnection and damping assignment--passivity based control，IDA-PBC)以最优控制的观点来研究如何调整IDA-PBC的参数，使其控制性能达到最佳.

本文将利用基于系统的电磁能和机械能来构造控制器设计技术-受控拉格朗日函数(controlled Lagrangians，CL)法[14].该方法已发展为与端口受控的耗散哈密顿系统数学上等价的方法[15]，两者相比，CL法的数学形式更简单、物理意义更明确、易理解.CL法从欠驱动力学系统角度来分析PMSM系统，使受控系统从形式上保持拉格朗日力学结构，得到光滑非线性反馈控制律，具有较大收敛范围，并且有助于实现CL法鲁棒控制和最优控制.与文献[8]相比，本文得到的光滑非线性反馈控制律可同时实现位置与速度的全局渐近镇定，而文献[8]却没有实现.

2 符号介绍

本文为书写方便，将首次出现的函数和矩阵注明自变量，下文再出现时将省略.Nn表示前n个自然数;对于i∈Nn，定义集合Ni={1，…，i};用x(q)表示向量q=[q1q2q3]T的函数，yi表示函数向量Y(q):R3→R3的第i个分量，其中:i∈N3;Zjk表示函数矩阵Z(q)的第j行第k列的元素，Zjo和Zok表示其第j个行向量和第k个列向量;I表示三阶单位矩阵，并定义如下符号:

对于同时具有上下标的符号，实行上标优先原则.

3 PMSM数学模型

设PMSM系统的广义坐标为q=[q1q2q3]T，其中:q1，q2分别为d轴和q轴的电感电荷，q3为电动机机械角位移;广义速度坐标为其中:分别为d轴和q轴的电感电流，表示机械角速度;u=[u1u20]T为d轴和q轴的原始控制输入，并且u=O(q)v，其中输入耦合矩阵O=[Io1Io2]，v∈R2，

假设PMSM系统产生的磁动势沿气隙圆周按正弦规律分布;磁路线性且不考虑磁路饱和;忽略系统的涡流、磁滞损耗、则PMSM系统在两相旋转d-q坐标系下的原始方程[10]为

式中:L1，L2分别为定子在d轴及q轴上的电感分量;J为系统的转动惯量;为负载转矩，其中:T1表示空载转矩与电机外加负载转矩之和，=Hq3表示电机与机械负载之间用相对较长的轴连接时产生的扭转矩，其中H为变形系数;np为极对数;ψ0为永磁体.

式(1)可简写为

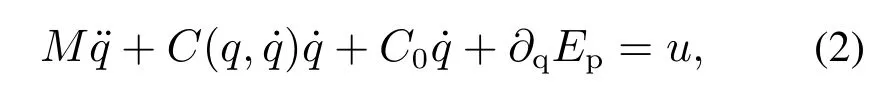
4 基于受控拉格朗日函数的PMSM系统控制器设计

4.1 构造受控能量和广义力

根据式(2)，将线圈绕组和永磁体产生的电磁能与转子产生的动能两者之和作为系统的受控动能:将负载转矩产生的机械能作为系统的受控势能:广义力则系统的受控拉格朗日函数和受控能量Ē如下所示:

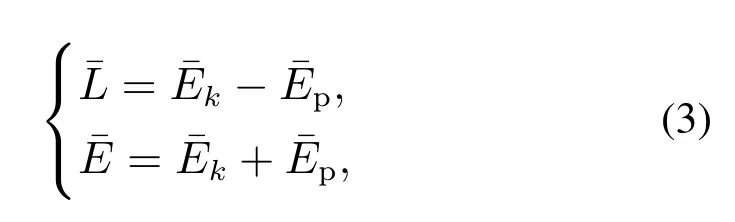
由式(3)-(4)可得

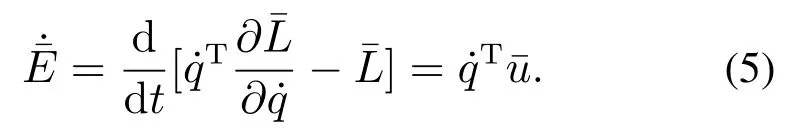
其中:g1，…，g9为关于q的函数，g10，g11，g12为常数.

注1由于原始系统中存在项，为与之匹配，在保守力矩阵G的各元素中引入常数项g10，g11和g12构成速度一次项的保守力.

即PMSM系统的受控能量是衰减的.

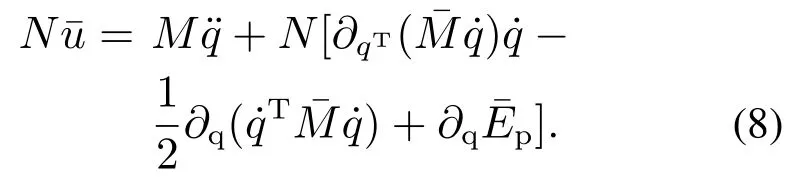
根据式(9)和文献[14]的式(9)-(14)可得

4.2 确定匹配条件

如果受控方程式(4)与原始方程式(2)相匹配，则由式(9)确定的控制输入是成立的，即u3=0对任意的(q，)都成立.

方程(13)-(18)因只和动能相关，故被称为动能方程(K方程).同理，式(19)被称为势能方程(P方程).对式(13)-(18)分别乘以后求和，可得一个与保守力项无关的K方程:

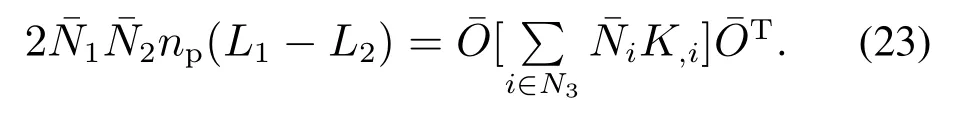
综上所述，将式(13)-(22)以及|K|/=0合起来即为受控方程与原始方程匹配的条件.

注2式(19)(23)为偏微分方程，与保守力项有关的方程(13)-(18)以及式(20)-(22)为线性代数方程组.因此，先求解难解的偏微分方程，后面求解代数方程.

4.3 确定匹配控制器

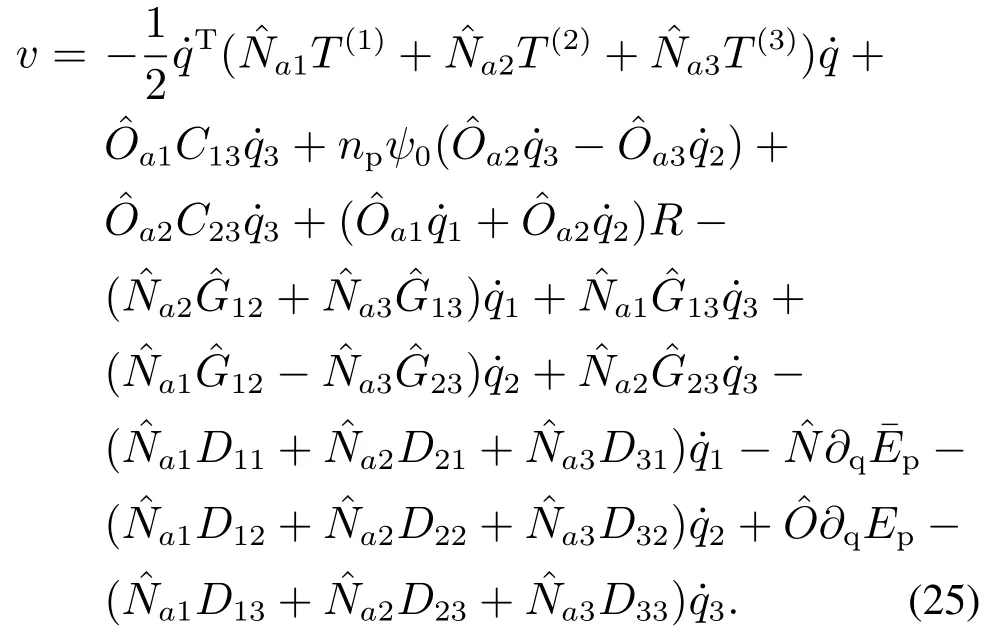
5 求解匹配条件

对于PMSM系统，第a个自由度有控制输入作用(ua/=0);第3个自由度无控制输入作用(u3=0)，故a∈N2.相应地，并将前面文中出现的一些符号变为

引入函数向量ΓT=-N3o/N33.由N，的定义可得K3o=-N33ΦT(q)，其中ΦT=[Φ1Φ2Φ3]=ΓTM，相应地有K3a=K33Φa/Φ3.为保证K ＞0，通常选取其中ka，ka+n为常数.

用Γ，K33以及表示的K方程和P方程以及与耗散力相关的方程如下所示:

令Γ1=0，Γ2=0，Γ3=-1，则可得式(27)即K33的一特解:

其中k3为常数.

系统的K矩阵为

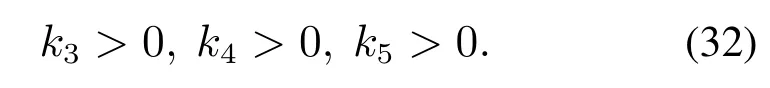
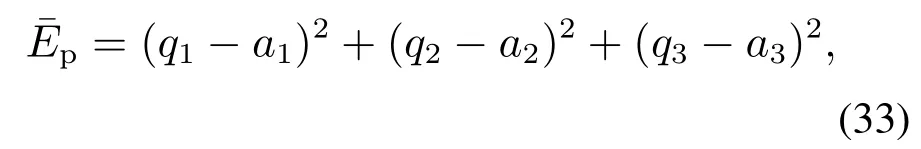
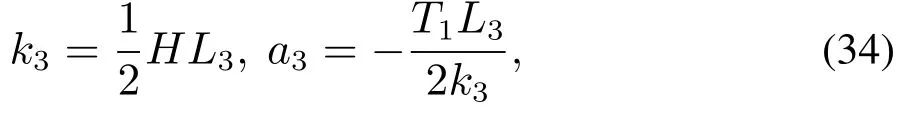
其中a1，a2，a3为常数.

由式(29)可得

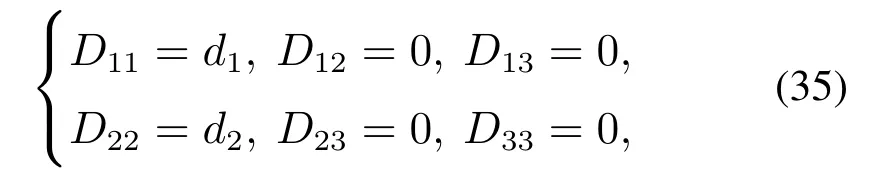
其中d1，d2为大于零的任意值.

6 确定匹配控制律及稳定性分析

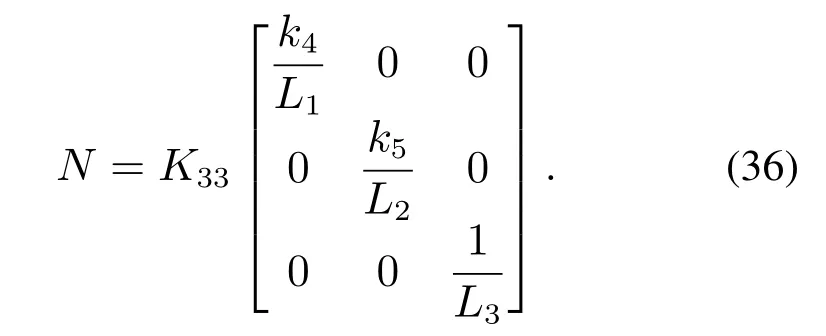
因为T(i)=其中i∈N3.故由式(31)和矩阵T(i)可得

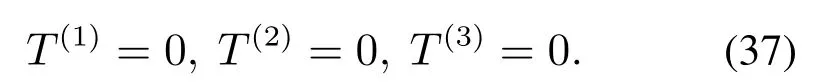
由式(13)-(18)，(20)-(22)(26)(36)得到系统匹配条件中保守力分量函数的解为

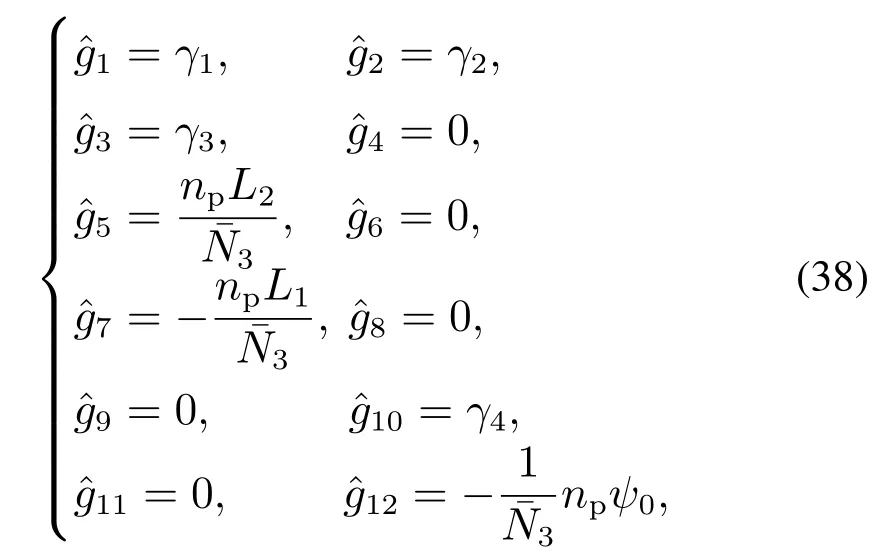
式中 γ1，γ2，γ3，γ4为任意值.

注3通过观察可知，与保守力相关的方程为含有7个独立方程的线性方程组.方程组共有12个变量，其中7个独立变量，5个自由变量.因此，式(38)只是其中的一个解.根据式(38)可知，匹配条件有大量的解，故与之对应的匹配控制器也有大量的解.

将式(26)(33)(35)-(38)代入式(25)可得系统的具体匹配控制律:

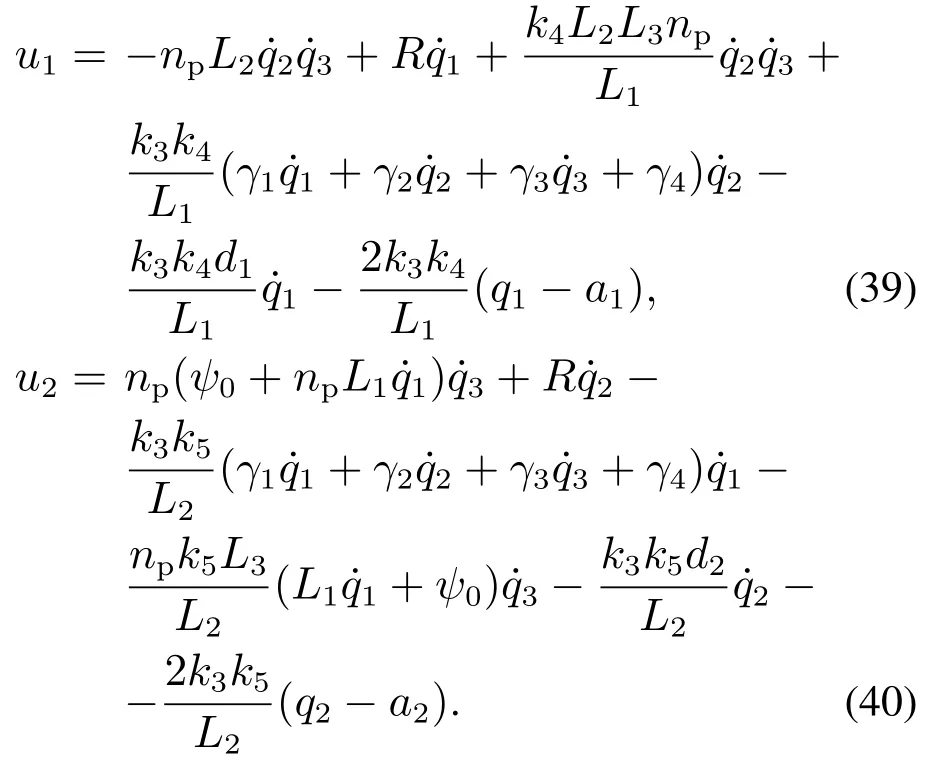
根据以上分析给出以下稳定性结论:

命题1对于PMSM系统，其控制器参数按如下选取:

则由式(39)-(40)确定的光滑反馈控制律可使PMSM系统在(，0T)实现全局渐近稳定，其中为受控势能的极小值点(a1，a2，a3).

证选取受控能量Ē作为Lyapunov函数V.若式(41)成立，则V 正定.根据式(7)，则有≤0.故由式(39)-(40)所给的控制律可使PMSM系统在期望平衡点实现全局稳定.

假设在该集合中存在这种轨迹，则由˙V=0可知轨迹上存在以下等式:

在轨迹上应存在某点q0，进而在该点q0的某个领域δ0内也成立，其中qd/∈δ0.沿轨迹对式(42)进行微分和积分可得

其中α和β为常数.

将式(39)-(40)(42)-(43)代入式(1)，可得

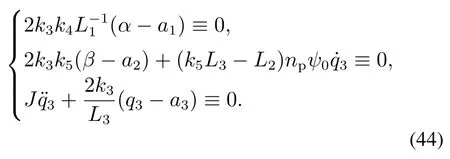
由式(44)可得到，当

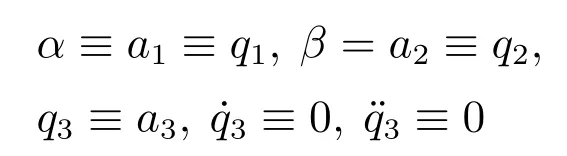
7 仿真结果分析

系统仿真参数按如下选取:d-q轴电感电荷分别为L1=4.5 mH，L2=3.2 mH;负载转矩T1=8 Nm;变形系数H=8;转动惯量J=0.002 kg·m2;平衡点a1=1，a2=1，a3=-1;极对数np=8;永磁体磁通ψ0=0.4 Wb;定子电阻为R=0.97 Ω;控制器的系数为

仿真结果如图1-4所示.

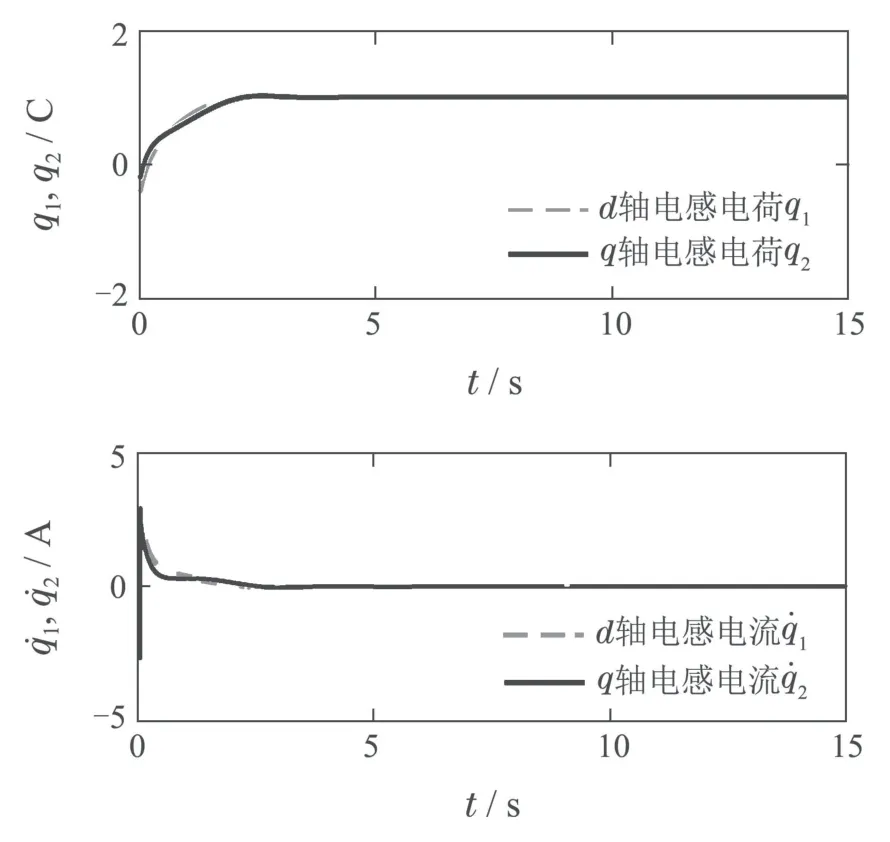
图1 d-q轴电感电荷和电流Fig.1 d-q axis inductance charge and current

图2 转子角位移和角速度Fig.2 Rotor angular displacement and angular velocity

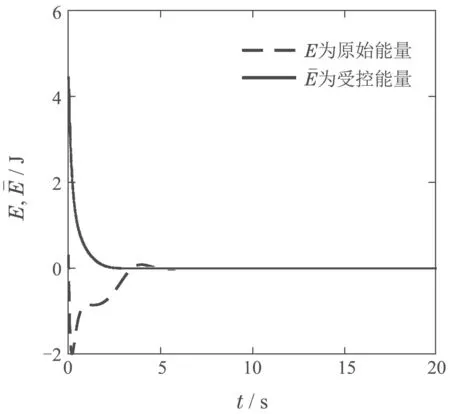
图3 原始能量和受控能量Fig.3 Original energy and controlled energy

图4 电磁转矩和控制输入Fig.4 Electromagnetic torque and control input

根据文献[16]可知，PMSM的电磁转矩的表达式为Te=其中F表示与转速成正比的阻尼系数.交流电机在一般的调速控制情况下并最终到达稳态时，系统的加速度为零.而负载转矩T1，角位移q3以及角速度都不为零，从而根据电磁转矩的表达式可知其亦不为零.而在本文中，当系统运行到达期望的位置平衡点时，广义速度的一次项以及与之对应的加速度都为零，故电磁转矩为Te=T1+Hq3=T1+Hqd=0.

8 结论

本文将CL 法应用到高阶、强耦合、非线性的PMSM的控制问题中.根据期望的受控能量及其时间导数来构造CL和广义力，通过它们得到系统的受控方程.其中引入速度一次项的保守力，得到原始方程与其相匹配的条件.通过求解匹配条件中的偏微分方程，得到与之相匹配的具体控制律.该控制律可同时实现位置与速度的全局渐近镇定;最后以正定的受控能量作为Lyapunov函数给系统稳定性证明带来极大简便.CL法从欠驱动力学系统角度来分析PMSM系统，使受控系统从形式上保持拉格朗日力学结构，可得到非线性光滑反馈控制律，具有较大收敛范围，并且有助于实现鲁棒控制和最优控制.因此，笔者下一步还可通过借鉴一般哈密顿系统的鲁棒控制来研究鲁棒CL 法.