牟方厉，吴 丹，董云飞

(清华大学机械工程系，北京 100084)

1 引言

机器人技术结合了当代机械工程、自动控制、材料、计算机、生命科学等多学科的发展成果，是本世纪伟大且具有代表性的技术成就之一.机器人系统是一个具有高度非线性和不确定性的复杂系统，机器人的控制系统是它的核心，机器人控制中的一个重要问题是通过给定各关节力矩使得机器人关节状态跟踪理想轨迹.目前对机器人控制方法的研究已取得了丰富的成果，常见的控制算法有计算力矩法、前馈补偿法、PID控制、鲁棒控制、自适应控制、模糊控制、神经网络控制、迭代学习控制、滑模控制和反演控制等[1-3].

然而，实际机器人系统受到系统建模精度，环境不确定性，参数辨识能力，计算实时性等诸多方面因素的制约，因此依赖于系统数学模型的大多数现代控制理论方法目前仍未在实际机器人系统中得到广泛的应用.比例积分微分(proportion integral differential，PID)控制器由于具有不基于被控过程的模型，结构简单，易于实现等优点，仍是当前机器人系统(特别是关节层面)中最为主要的控制器形式.然而，受制于控制律形式，PID控制器将很难让受控机器人兼顾良好的动态性能和静态性能，尤其当需要机器人执行高速、大范围运动时，PID控制将不再有效甚至导致受控系统的不稳定[4].

自抗扰控制技术(active disturbance rejection control，ADRC)是韩京清教授于20世纪90年代末期，基于PID控制思想提出的一种新型控制方法[5].自抗扰控制器不依赖于系统精确的数学模型，以扩张状态观测器(extended state observer，ESO)为核心，利用扰动估计，状态误差反馈和扰动补偿等方法在系统输出产生影响之前实现对总扰动的主动补偿[6].自抗扰控制器设计时只需要知道系统的阶次和输入输出通道等少量系统信息，具有强抗扰能力和强控制鲁棒性等优点，近年来在伺服控制系统[7]、工业过程控制[8]、航天航空[9]等领域内得到了广泛的应用，具有良好的工程应用前景.

而与前述领域相比，ADRC在机器人控制上的应用目前还较少.Castaneda等[10]设计了基于ADRC的自适应控制器，用以求解具有不确定动力学模型的Delta并联机器人的轨迹跟踪问题.Nadhynee等[11]研究了基于扰动估计的两足机器人鲁棒控制问题，提出了一种基于高增益类线性扩展状态观测器的鲁棒控制器来实现扰动消除.Castellanos等[12]基于ADRC设计了一种用于踝足矫形器(ankle foot orthosis，AFO)的步态跟踪控制器.Yi Long等[13]提出了一种基于自抗扰控制的应用于下肢康复外骨骼的步态跟踪策略，数值仿真和实验结果均表明采用ADRC控制方法的康复系统能比传统PID控制更准确地跟踪目标的步态.Ren等[14]针对协作机器人系统利用ESO提出了一种基于本体传感器(编码器和扭矩传感器)的碰撞检测方法.

以上研究展示了ADRC在机器人控制中的应用潜力，但是对于具有高速、高精度要求的机器人关节控制器，控制参数整定等控制器设计方法上仍需要进一步的研究.对机器人进行动力学前馈可以在提高稳态、动态性能的同时减少控制器设计和整定难度.机器人动力学前馈方法主要可以分为两类:一类是基于动力学建模和动力学参数辨识的计算力矩方式[15]，如何构建准确的模型和设计有效的辨识算法是此类方法的关键;另一类是基于机器学习的数据驱动方式[16]，确保得到的系统稳定和避免参数过学习是该类方法的重点.本文将上述两类方法进行了结合，在动力学建模和辨识的基础上搭建了一个对建模误差和不确定进行补偿的深度神经网络，以此来进一步提高控制性能.

本文针对机器人关节控制器展开研究，提出了一种基于ADRC的机器人关节控制器，构建Lyapunov函数证明了该控制器的稳定性，基于遗传算法(genetic algorithm，GA)完成了控制器参数的整定，在动力学建模和参数辨识的基础之上设计了一个多层感知器(multilayer perceptron，MLP)网络以完成对动力学建模不确定性的补偿.最后，对提出的控制方法性能进行了仿真分析和实验验证.

2 机器人模型

一个具有N自由度的串联机器人如图1所示.其动力学模型可由以下的二阶微分方程描述[17]:

图1 N自由度串联机器人模型Fig.1 Model of a N-joint robot

记x1=q，u=τ，则控制对象(1)可以描述为

为便于后续控制器设计，下文忽略各关节间的耦合影响，采用模组设计思想对每个关节进行独立的控制器设计.此时每个关节的控制对象均为如下形式:

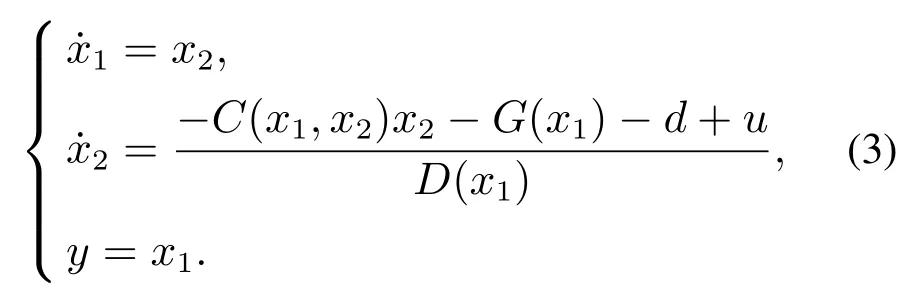
3 关节自抗扰控制器设计

自抗扰控制器主要由生成过渡过程(微分跟踪器(tracking differentiator，TD))、扩张观测器(ESO)、误差反馈律和扰动补偿这几部分组成.以二阶控制对象和三阶扩张观测器为例，自抗扰控制器的结构可由如图2所示.

图2 自抗扰控制器结构Fig.2 Diagram of ADRC for second-order systems

图中:v为期望输入;u为系统控制输入;uf为前馈补偿输入;y为系统实际输出;v1为v的过渡过程;v2为过渡过程的微分;e1，e2为过渡过程信号与观测信号的误差函数;u0为中间控制量;z1，z2，z3为系统状态的观测量;b0为增益参数.

ADRC的离散表达如下:

1) 以控制目标v0为输入的TD微分器.

2) 以控制输入量u和系统输出y为输入估计系统状态和扰动的扩张状态观测器.

3) 误差反馈律和系统扰动补偿:

其中:fhan为最速控制函数，其具体形式可见文献[5];h为系统采样步长;r0为速度因子;g1(e)，g2(e)，g3(e)为扩张观测器反馈函数;fcon(e1，e2)为控制律函数;β01，β02，β03，b0为控制器参数.

本文设计的ADRC控制器为机器人关节位置控制器，其输出控制量为关节电机的期望力矩.将系统(3)中存在的非线性部分、动态时变特性以及运行过程中系统存在的扰动整合为总扰动

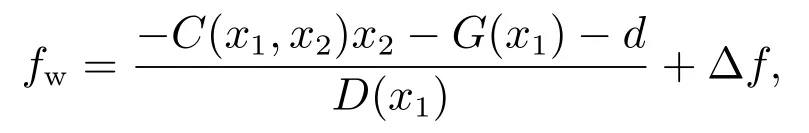
并将fw扩张为新的系统状态x3，此时系统扩张为如下的线性控制系统:

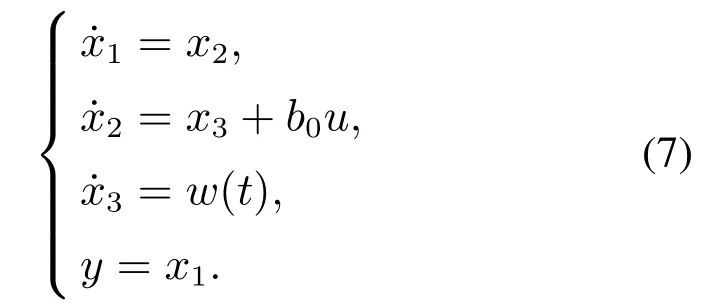
使用以下形式的三阶线性ESO对扩张系统进行估计和观测:

结合TD跟踪器和ESO观测器，可得到以下表达，其中:r1，r2为反馈律误差函数，e1，e2，e3为观测误差函数.

由系统方程(7)，ESO方程(8)和式(9)可得到如下线性观测器误差系统:

定义如下系统状态与给定信号的误差函数s1，s2:

根据式(6)，使用如下形式的误差反馈控制律:

由式(7)(10)-(11)，可得到误差系统

定理1考虑对系统(7)构建的ESO系统(8)，在总扰动fw连续可微的假设下[18]，当β01，β02，β03＞0，β01β02＞β03时，可以保证该观测器误差系统是渐近稳定的.

证记Y=E=[e1e2e3]T，ue=w，有

式中:

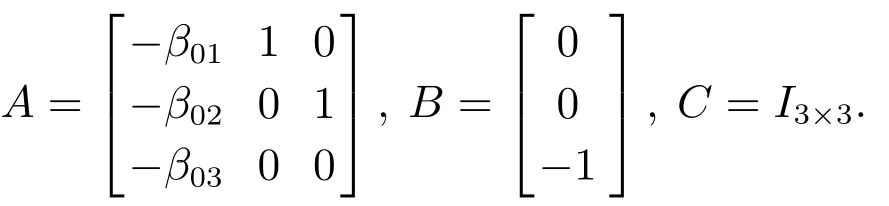
系统矩阵A的特征多项式为

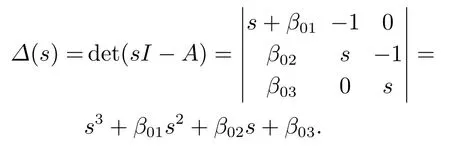
当β01，β02，β03＞0，β01β02＞β03时，系统稳定且状态完全可控可观，并有

根据文献[3]，提高β01，β02，β03可以减小对扩张状态的观测误差并提高观测器的收敛速度，但相应的观测器对测量噪声将更加敏感.在初步设计时可通过近似选取β01=3ωo，将参数调节转换为观测器带宽ωo的选择.

定理2考虑闭环系统(13)，线性ESO(8)和误差反馈控制律(12)，通过调节合适的参数k1和k2，可以保证这个闭环系统(13)是大范围一致渐近稳定的.该定理的具体证明过程可见文献[19].

根据文献[4]，k1，k2的调节原则可以与对应的比例微分(proportion differential，PD)控制器整定过程类似，通过提高k1来加快响应与减小残差，通过提高k2来加快响应与减小超调，且越大系统的相对稳定性越高.

4 控制参数的优化设计

从上节分析可知，与PID控制相比，ADRC的控制参数数量较多，TD跟踪器中的参数有速度因子r0和滤波因子h0;ESO中的参数有β01，β02，β03，b0;误差反馈律中的参数有k1，k2，b0.这些控制参数的选择将对系统的控制性能产生较大的影响.

在这些参数中，速度因子r0和滤波因子h0可以根据实际控制器对快速性的需要和系统能提供的最大加速度进行设置.

机器人关节控制器处于机器人控制架构中的底层，故控制器参数整定应尽可能的离线完成以减少在线调参可能带来的风险.下文在对ESO和误差反馈律的控制参数设计时依据ADRC的分离性原理，即先基于系统响应分别完成对扩张观测器和误差反馈律进行设计，再根据完整闭环系统进行参数的调整.

本文利用遗传算法(GA)对剩余控制参数进行离线优化以实现最优控制，该过程仅需要基于一能实现系统稳定运动的激励源.本文的激励源为一简单设计的PID控制器(由于该控制器只需要考虑稳定性，故设计和实现十分容易)完成系统响应数据的采集.完整的参数设计过程如下:

算法1ADRC控制参数优化过程:

1) 设计一稳定的激励源(文中为PID控制器0);

2) 采集在控制器0运行下系统的控制输入和系统响应;

3) 根据2)中结果离线优化ESO参数;

4) 根据2)中结果离线学习系统模型;

5) 基于3)-4)中获得结果离线优化误差反馈律参数;

6) 将上述离线优化得到的参数根据闭环响应进行调整.

在ESO参数设计中使用遗传算法进行离线优化，优化变量为β01，β02，β03，b0，ESO的目标是通过输出信号根据控制输入信号重构系统状态，为使得获得的ESO具有快速估计系统状态的能力，对于文中系统，其观测状态为关节角度、关节角速度和关节角加速度.因此一个良好的ESO将同时具有更小的角度观测误差和角速度观测误差，故在此使用误差绝对值积分J1作为优化指标

单纯使用J1作为优化目标可能导致过大的ESO参数β01，β02，β03，这意味着过高的观测带宽.由于学习数据为PID控制下的实验结果，故ESO的最大加速度补偿输出应与PID控制量较为一致，为了提高得到的ESO对噪声的抑制能力并使优化中控制参数不会无限制增长，使用J2对优化函数进行正则

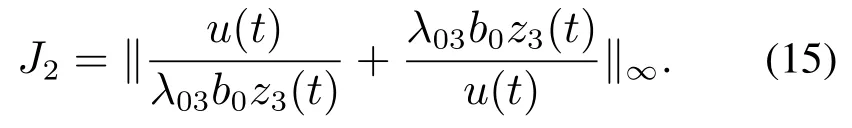
将上述指标函数进行加权组合，得到系统目标优化函数J为

则该优化问题可由下式表述:

类似地，在误差反馈律参数设计中构建的优化函数Je为

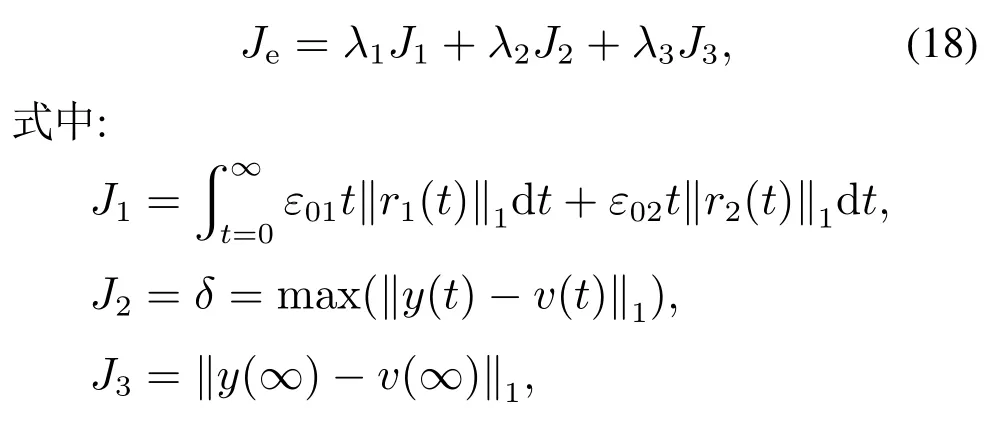
其中:J1主要反映了整个过程的快速性，J2体现了跟踪过程的超调量，J3反映了最终的稳态误差，一个良好的控制律应使被控对象同时具有快速性、小超调和低稳态误差.相应的优化问题为

5 动力学前馈补偿

5.1 动力学建模与参数辨识

本文的建模过程采用Lagrange方法，通过构建参数集将式(1)的动力学模型转化为如下的基本参数集表述形式:

式中:KKK∈Rm×1(m ＜10n)为基本参数集;∈Rn×m为对应的回归矩阵;τf∈Rn×1为关节摩擦力矩.文中采用的关节摩擦模型为如下的库仑-粘性摩擦形式:

参数辨识的目标即为利用机器人跟踪激励轨迹的过程数据估计出基本参数集KKK和摩擦参数集{fc，fw}，参数辨识过程详见文献[20].

实验中采用的激励轨迹为基频0.01 Hz，20阶次叠加的傅里叶轨迹，实验使用的6自由度机器人(图7所示)模型的基本参数集维度为22，摩擦参数集的维度为12.实验中关节输出扭矩是通过测量关节电流而间接获得的，该转换操作已由设备厂商封装好，实际上位机中可直接从数据帧中得到各关节的力矩值.

实验中使用滑动平均法进行辨识前的数据预处理，整个模型辨识过程在MATLAB环境下离线完成，对一次实验数据进行辨识的时间消耗大约为25 min，使用多组辨识轨迹的辨识平均值作为最终的辨识模型.辨识结果如图3所示.

采用关节误差力矩的均方根误差E1和最大关节误差力矩比E2作为辨识精度指标，它们分别反映了平均辨识精度和最大辨识误差水平，其定义如下:

式中:τr(i)为第i个数据点的测量力矩值，τp(i)为该点对应的预测力矩值.参数辨识结果如表1所示，其中均方根误差E1的单位为Nm，最大关节误差力矩比E2为无量纲的比值.

图3 关节力矩预测值与测量值Fig.3 Prediction and measurement of the joint torque

表1 参数辨识结果Table 1 Parameter identification results

5.2 MLP补偿网络

上述辨识误差主要来源于建模误差、系统中难以建模部分和参数的不确定性.为减少补偿误差、进一步提高控制性能，本文构建了一个MLP补偿网络来完成对关节误差力矩的实时估计与补偿.该网络的输入为一定时间T内(实验中为连续10个采样周期)的各关节位置、速度信息，输出为各关节相应的误差补偿力矩.

基于辨识模型和MLP补偿网络的完整补偿流程如图4所示，最终获得的动力学前馈力矩τfw为辨识模型的计算力矩τ1和MLP网络补偿力矩τ2之和，即τfw=τ1+τ2.这种方式可以结合动力学建模具有的可靠性及物理意义和深度神经网络具有的强大学习能力，减少神经网络所需的输出值和学习负担以及神经元产生饱和的可能.

该MLP补偿网络的具体结构如图5所示.该网络拥有4个隐层，层间均加有Dropout以减少过学习，激活函数均为Relu 形式，共计24，710个学习参数.该网络在单个GPU环境下网络训练时间约为1 h，对输入进行一次预测的时耗约45 μs.

图4 动力学前馈补偿流程Fig.4 Dynamic feedforward compensation process

图5 MLP补偿网络结构Fig.5 Structure of MLP network

对相同测试数据同样采用关节误差力矩的均方根误差E1和最大关节误差力矩比E2作为精度指标，结果如表2所示.

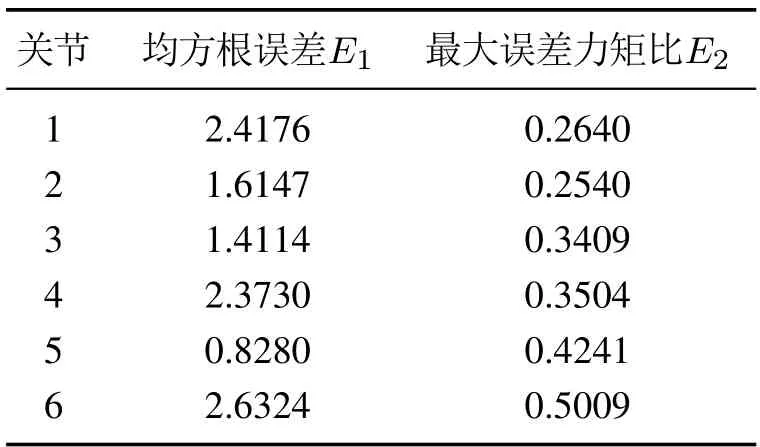
表2 采用MLP补偿后结果Table 2 Results using MLP compensation

从表中结果可知，采用MLP补偿网络后各关节误差力矩的均方根误差E1得到小幅优化(约0.1～0.4 Nm)，而各关节最大误差力矩比E2均得到较大程度的改善(10%～30%)，可见使用MLP补偿网络可以在不过度增加计算时间消耗的前提下减小辨识误差，使补偿力矩的可信度和精度均得到了提高.

6 数值仿真及实验验证

6.1 数值仿真结果

仿真环境为MATLAB Simulink，在仿真中使用的模型物理参数为D=4，C=0.01，I=3.7.广义扰动项d由d1，d2，d33部分构成，其中:d1为摩擦项;d2为噪声项;d3为施加的系统扰动项，在仿真过程中扰动项d1，d2总是存在，控制力矩输出限制为15 Nm.GA优化参数中种群大小为400，最大迭代次数为400，交叉率为0.8，变异率为0.2，个体迁移率为0.2.ESO优化权值为λ1=1，λ2=2，控制律优化权值为λ1=1，λ2=1.5，λ3=100，利用相同的优化目标函数和优化参数分别对PID控制器和ADRC控制器进行参数优化设计.

当不存在系统扰动项d3，跟踪的期望轨迹为幅值等于10°的阶跃信号时，仿真结果如图6(a)所示.从仿真结果可知，使用文中设计的ADRC控制器可以获得比bang-bang控制器和PID控制器更好的控制效果，在实现关节快速稳定的轨迹跟踪的同时具有良好的控制精度.

图6 系统在不同扰动下关节控制效果对比Fig.6 Joint trajectories of the robot under different forms of disturbance

图6(b)-6(c)展示了上述控制器在系统施加有不同形式系统扰动项d3下的控制效果.图6(b)给出了在外部施加正弦扰动力矩下系统的控制效果.图6(c)给出了在系统存在内部扰动下控制器的控制效果.从仿真结果可知，文中设计的ADRC控制器具有很好的鲁棒性和较强的扰动抑制能力，不论该扰动是外部扰动还是内部扰动.

6.2 实验结果

通过仿真研究验证了所设计的关节ADRC控制器的可行性和抗扰能力，为进一步考量该方法在工程应用中的有效性与实用性，在机器人系统实验平台上进行验证.

实验中使用的机器人为图7所示的大族6自由度机器人，使用具有RT内核的ROS环境完成算法1 kHz的实时运行，使用EtherCAT进行通信.在数据采集阶段采用的PID控制器参数为P=10，I=0.1，D=5.优化过程和优化中使用的各项参数与上节的仿真中一致.

图7 六自由度实验机器人Fig.7 Six degrees of freedom experimental robot

实验中各关节的期望跟踪轨迹信号为幅值大于10°的阶跃函数，经过优化设计得到的ADRC控制器与机器人自带PID控制器的对比实验结果如图8所示.

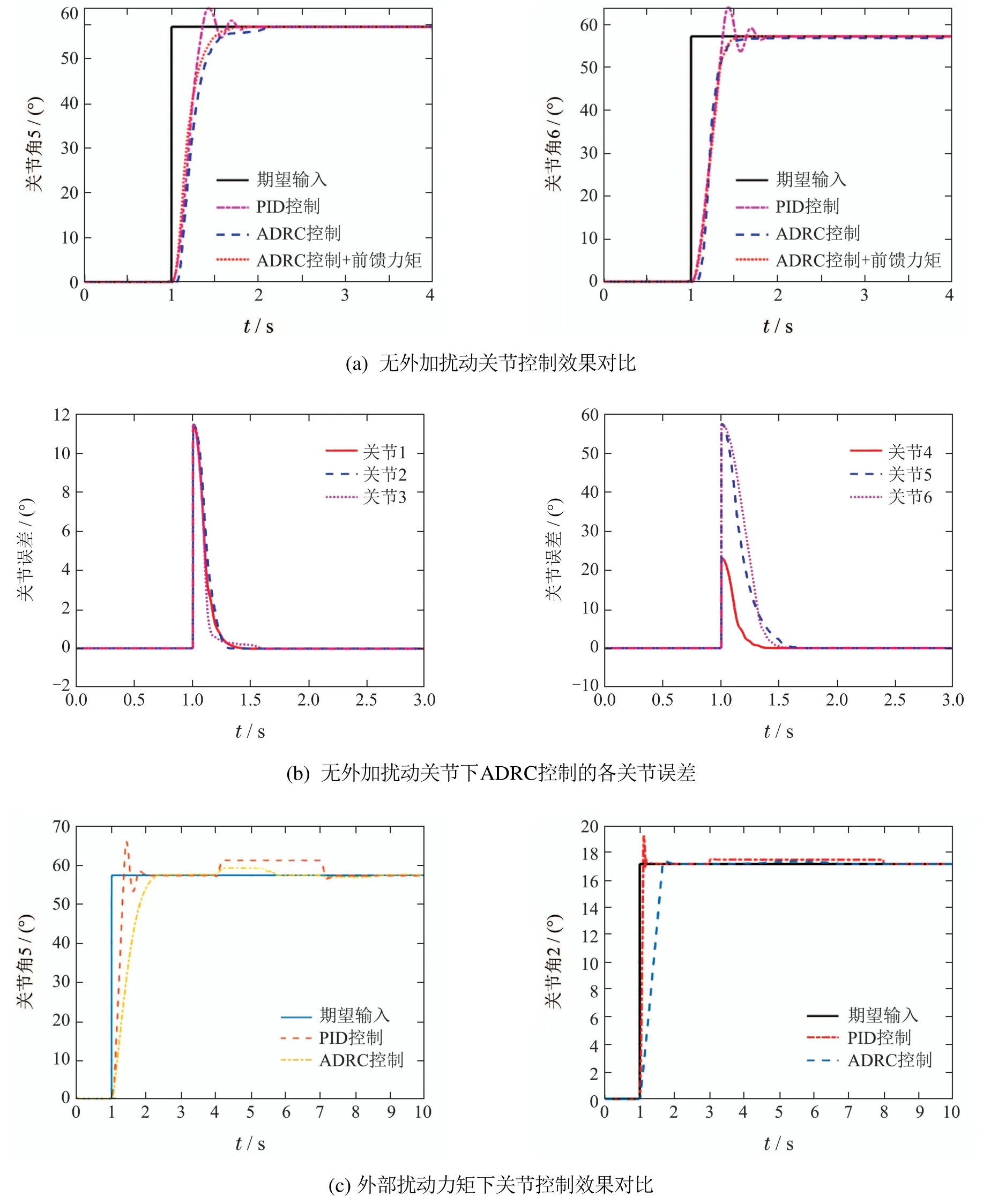
图8 实验机器人关节控制效果对比Fig.8 Response performances for different controllers of experimental robot

图8(a)给出了机器人各关节的控制效果对比情况，图8(b)给出了在文中设计的ADRC控制器下机器人各关节的跟踪误差曲线，图8(c)给出了机器人关节2和关节5在施加外扰动力矩下的效果对比.由实验结果可知，文中的ADRC控制器能控制实际机器人在约0.7 s内完成各关节大角度阶跃信号的高速平稳跟踪，实现无超调的目标关节角度转换，控制稳态精误差在0.012°之内，同时在受扰动下更快的完成扰动补偿.该控制器可以获得比传统PID控制器更好的控制效果，在实现关节大范围快速稳定轨迹跟踪的同时具有良好的控制精度和更强的扰动抑制能力.

7 结论

本文利用自抗扰控制算法实现了机器人的关节控制，该算法具有不依赖系统模型，抗干扰能力强，能兼顾动态性能和稳态精度，控制律设计较为简单等优点.针对受控机器人系统特性给出了一套实际控制器的完整设计方法与参数整定方法，根据控制指标设计相应优化函数并利用GA算法完成了最优控制参数的优化，在对机器人进行动力学参数辨识的基础上设计了一深度MLP网络完成对建模不确定性的实时补偿，提高了控制补偿精度与系统动态性能.仿真和实验结果均表明该控制算法能够实现机器人快速稳定的轨迹跟踪，具有良好的控制精度并有很强的抗干扰能力，此外该算法不依赖于精确的系统模型，对硬件系统的要求较低，能完成对机器人的实时控制，具有较强的工程应用价值.下一步研究将完善对控制律和控制参数的优化设计，并研究控制器在特定作业任务下的控制效果.