陈建勇，孙明轩

(1.浙江工业大学信息工程学院，浙江杭州 310023;2.温州科技职业学院信息技术学院，浙江温州 325000)

1 引言

迭代学习控制(iterative learning control，ILC)适用于处理具有重复运行特点的被控对象，是一种具备学习能力的高级控制技术.它以跟踪误差调整被学习信号，不断修正控制输入，使得受控对象在整个作业区间上实现对参考信号的完全跟踪.迭代学习控制方法要求系统满足严格重置条件，即每次迭代作业开始时刻的系统状态与期望状态初值保持一致.然而，受复位精度的限制，系统初态与期望初态不一致往往是存在的，这会降低闭环系统的跟踪精度.因此，初值问题是迭代学习控制领域需要解决的一个基本问题.目前，基于Lyapunov综合方法设计初态任意情形下的学习控制器是值得研究的课题，并已得到一些解决方案.文[1]针对一类模糊系统，引入时变边界层.由于边界层随时间单调递减，且收敛于零，则被边界层限定的跟踪误差也趋于零.文[2]利用时变边界层考虑了纯反馈系统的初态误差问题.文[3]提出初始修正吸引子概念，利用吸引子达到完全实际跟踪.文[4]利用变期望轨迹法，提出了D型、PD型和PID型学习算法，在迭代域上解决了参考轨迹慢时变的情况.文[5]构造了一种期望误差轨迹，首次提出误差跟踪设计方法.相比于变期望轨迹法，它不用每次迭代时重新设计初始段轨迹，只需要保证期望误差轨迹初值与实际误差轨迹初值一致即可，有利于拓宽学习控制方法的应用范围.

人们在设计自适应控制器或自适应学习控制器时，为了增强系统的鲁棒性，往往对控制输入或参数估计采取限幅手段，比如饱和函数或投影算子.然而，仅仅对控制输入或参数估计限幅是不够的，出于对设备运行安全方面的考虑，需要采取措施对位移-速度等系统状态进行约束.近年来，受重构Lyapunov函数思想的启发，障碍李雅普诺夫函数(barrier Lyapunov function，BLF)的约束控制方法因其无需知道系统的精确解而被广泛用来解决系统状态和系统输出的约束问题.文[6]针对含状态约束的Brunovsky标准型系统，首次以约束区间为定义域构造了Lyapunov函数并结合使用反推技术.文[7]给出了BLF函数的严格定义并研究了严格反馈输出受约束系统的控制问题.在已有的文献中，学者们已经提出了BLF 函数的3 种主要类型，包括对数型[8-9]、积分型[10-11]以及正切型[12-13].文[14]首次提出一种新的障碍Lyapunov函数:二次分式型BLF函数(quadratic-fraction BLF，QFBLF)，用于学习控制器设计.文[15]考虑非参数不确定系统的学习控制问题，利用QFBLF函数设计控制器，实现控制过程中的状态约束.尽管基于BLF思路解决系统状态和系统输出的约束问题已经有了一些研究成果，仍需要进一步深入探讨.

本文讨论一类严格反馈非线性系统的误差约束跟踪学习控制问题.拟构造BLF函数的两种形式:二次分式型对称BLF函数和二次分式型非对称BLF函数来分别设计控制器.分析表明，两种控制方案均能实现跟踪误差囿于预设的界内，进而实现迭代过程中对系统状态的约束.

2 问题提出和准备

考虑在时间区间[0，T]上重复运行的严格反馈非线性系统:

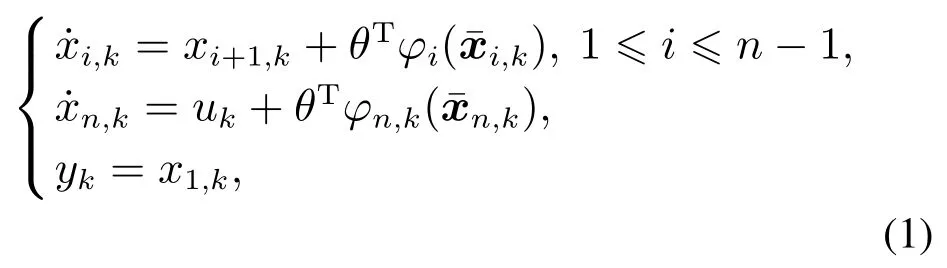
式中:k(=1，2，…)表示重复作业次数;xi，k∈R为系统状态且分别为系统输入和系统输出;θ∈Rn是未知参数;是已知光滑函数，记给定[0，T]上的参考信号r1(t)，满足1≤i≤n，且存在常数Mi，使得|ri(t)|≤Mi.

本文的控制目标是，设计学习控制器uk，使得迭代学习过程中跟踪误差囿于预设的界内，以实现系统状态约束;经过足够多次迭代，实现系统输出在指定作业区间上对参考信号的完全跟踪.

为表达简便，在不引起混淆之处，文中略去函数的时间自变量.

为了克服系统初态误差的不确定性，定义如下函数[5]:

其中:ek，εk是关于时间t的函数;是构造的期望函数，它包含用来表示误差衰减性态的函数ξ(t).对于ξ(t)的表达式，应是一连续可导的单调递减函数，且满足:1)ξ(0)=1;2)ξ(t)=0，∀t∈[t1，T]，t1＞0;3)ξ(j)(t1)=0，j=1，2.由条件1)和式(2)可知:εk(t)在t=0时，满足εk(0)=0，∀k.

对于式(2)，若ek代表误差函数，相应的可看作期望误差轨迹(函数)，它将在下一节的控制器设计中起到重要作用.

3 学习控制

为了设计约束学习控制器的需要，这里先给出二次分式型BLF函数的两种形式，具体如下:

1) 二次分式型对称BLF函数的典型形式为

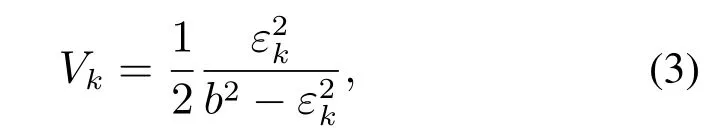
其中b ＞0.应用BLF函数(3)时，需假定实现时系统所受到的各种干扰无法使得|εk|＞b，否则会导致系统发散.

2) 二次分式型非对称BLF函数的典型形式为

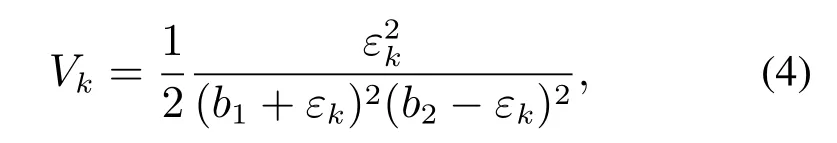
其中:b1＞0，b2＞0，且b1/=b2.

3.1 二次分式型对称BLF

针对系统(1)，本节应用对称BLF函数(3)，并结合反推技术来设计控制器:从步骤1到步骤n-1设计虚拟控制器αi，k;步骤n设计控制器uk.系统中的未知参数采用积分学习律进行估计.控制器具体设计过程如下:

定义状态误差

其中α0，k=0.

假设1存在已知的常数ηi满足

一般地，重复作业系统的复位点不一定与期望初态一致，但复位点落在以期望初态为中心的某一邻域内，这一点是可以被允许的，因此假设1是合理的.

步骤1迭代运行时，系统初态误差一般是存在的，定义跟踪误差

取虚拟控制

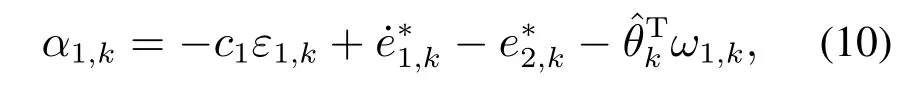
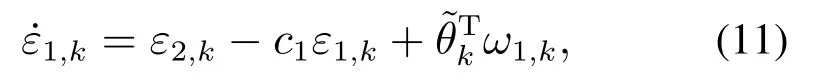
取如下对称BLF函数:

对V1，k求导，并将式(11)代入，得

步骤i(2≤i≤n-1) 类似于步骤1，定义跟踪误差

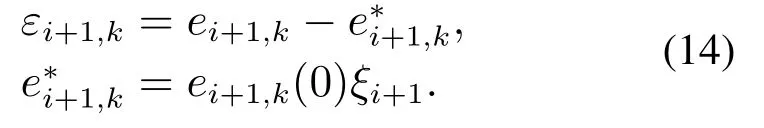
对εi，k求导，得

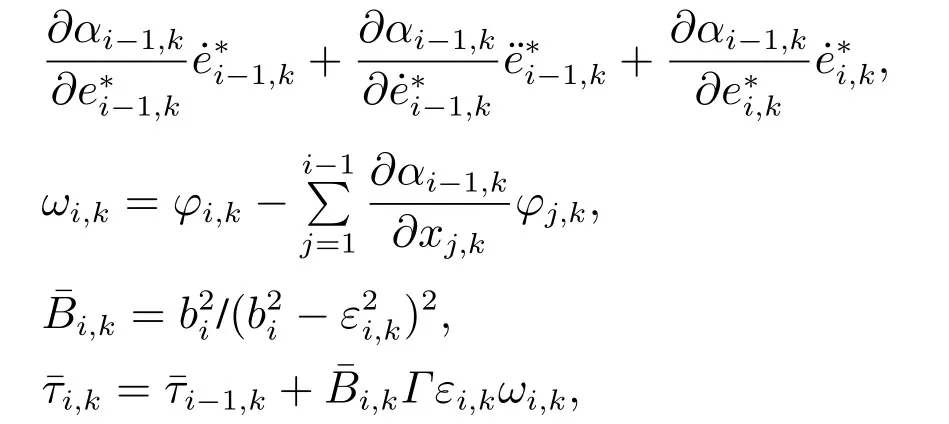
取虚拟控制

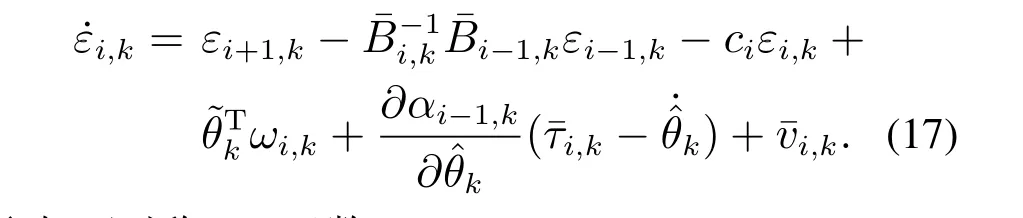
取如下对称BLF函数:

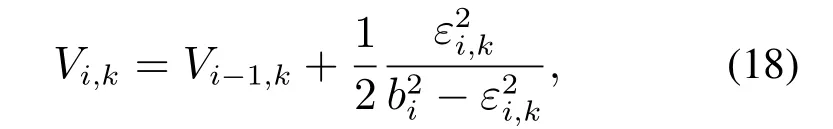
对Vi，k求导，将式(17)代入并化简，得

由于

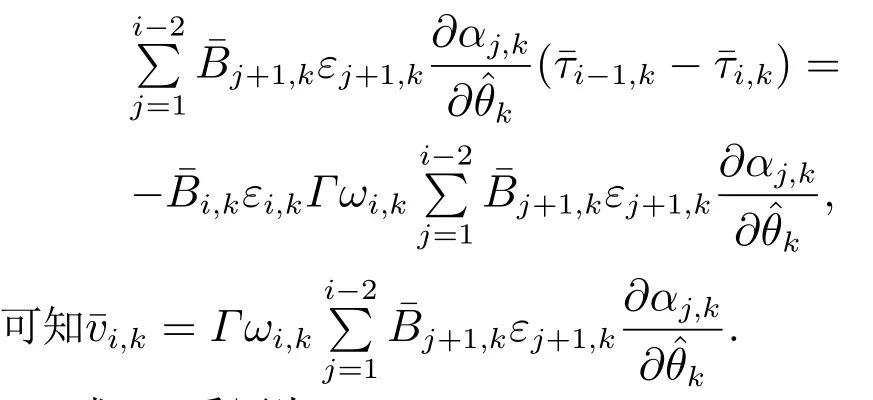
式(19)重写为

步骤n定义跟踪误差

对εn，k求导，得

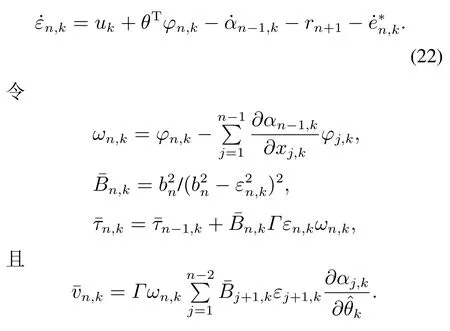
设计控制律

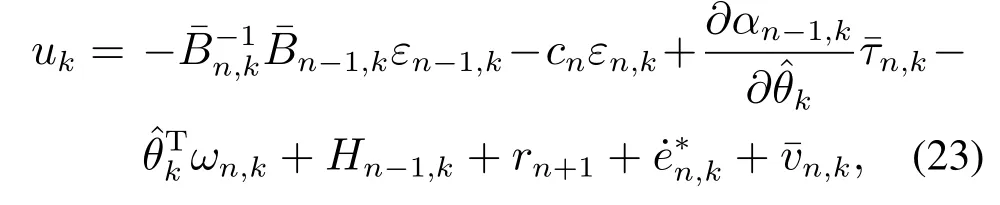
以及积分学习律

将式(23)代入式(22)，得

取如下对称BLF函数:

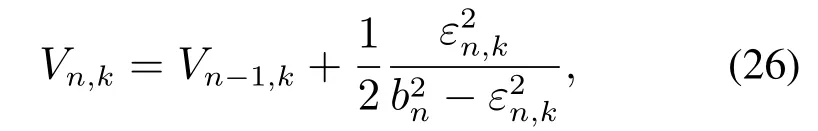
对Vn，k求导，并将式(24)-(25)代入，得

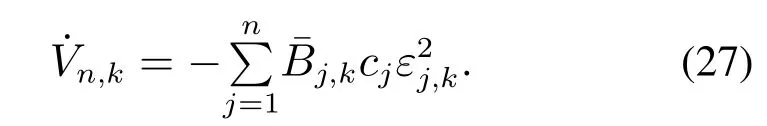
假设2对∀k，当t=0时，

定理1非线性系统(1)，满足假设1-2，采用控制律(23)以及积分学习律(24)，则系统有以下性质:

i) 系统中所有信号有界，且

ii) 保证迭代过程中，|εi，k|＜bi成立，同时系统状态有界约束始终满足.

证i) 变量有界性和系统收敛性.

根据假设2 可知‖εk(0)‖2=0≤‖εk(T)‖2，这里εk=[ε1，kε2，k… εn，k]T.由式(26)，得

把式(27)代入式(29)，并重复式(29)k次，得

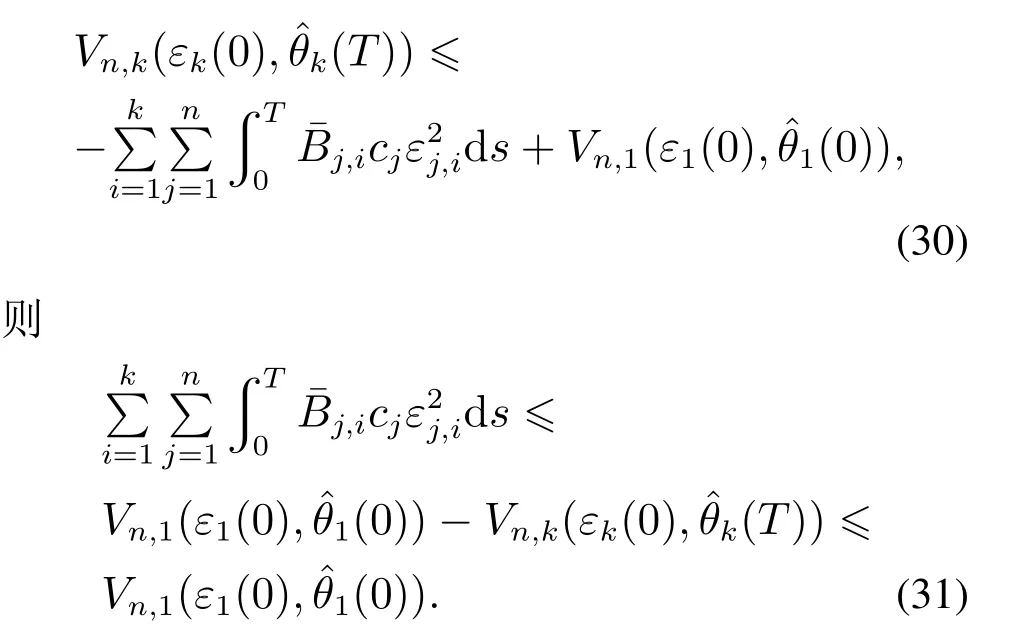
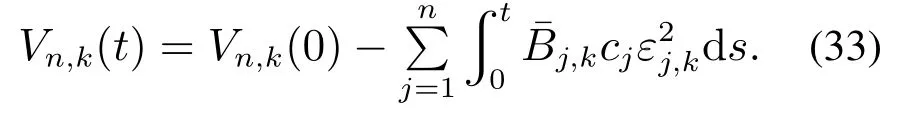
ii) 系统状态的有界约束.

根据式(27)，在各次迭代过程中，有|εi，k|＜bi.首先证明x1，k的有界约束.由于ξ1的单调递减性，由式(7)并结合假设1可知因为r1的有界性，可得

证毕.

由定理1可以看出，运用本节构造的二次分式型对称BLF函数，通过将εi，k囿于预设的界内，以实现对状态的约束.

3.2 二次分式型非对称BLF函数

被控对象中，系统状态约束不总是对称的，更多的是以非对称约束形式存在.因此，设计合适的非对称BLF函数更有实际作用.针对系统(1)，本节应用非对称BLF函数(4)，并结合反推技术来设计控制器.系统中的未知参数采用微分-差分学习律进行估计.控制器具体设计过程如下:

需要声明的是，本节控制器设计过程中使用到的一些变量标记及其含义与第3.1节的相同，此处不再重复描述，本节只写出一些不相同的变量.

步骤1令

取虚拟控制

将式(34)代入式(9)，得

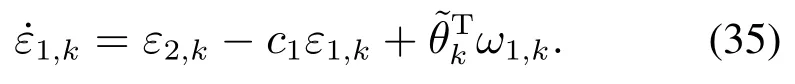
取如下非对称BLF函数:

式中 δ∈[0，1).对V1，k求导，并将式(35)代入，得

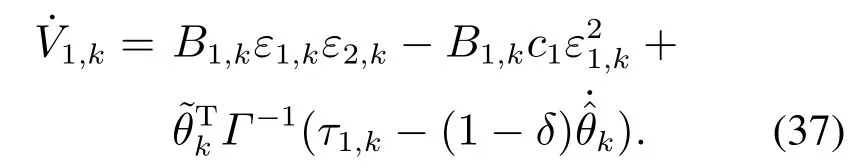
步骤i(2≤i≤n-1) 令

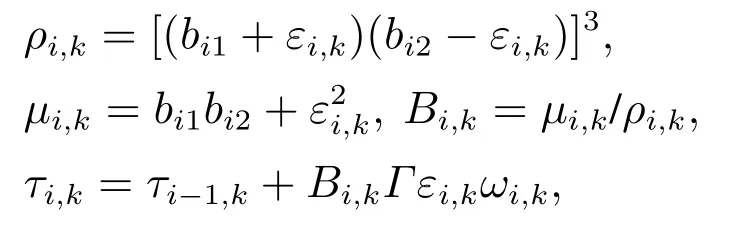
取虚拟控制

其中v2，k=0，而vi，k的设计类似于上一节的它的表达式将在下面给出.将式(38)代入式(15)，得

取如下非对称BLF函数:

对Vi，k求导，并将式(39)代入，得

要使βi，k=0，则vi，k的表达式如下:

由于

式(41)重写为

步骤n 令

设计控制律

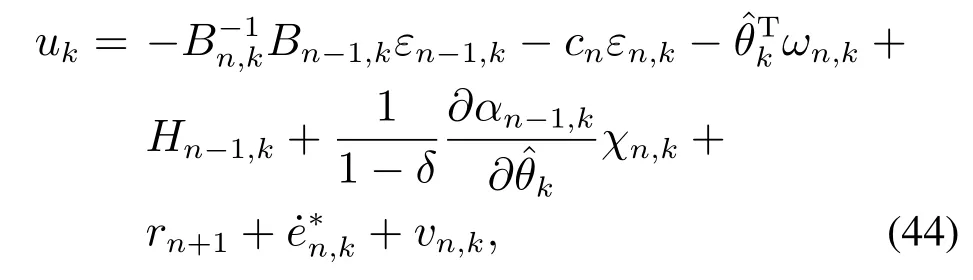
以及微分-差分学习律

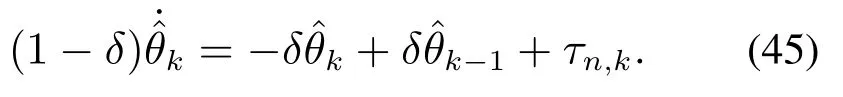
将式(44)代入式(22)，得

取如下非对称BLF函数:

对Vn，k求导，并将式(45)-(46)代入，得

定理2非线性系统(1)，满足假设1-2，采用控制律(44)以及微分-差分学习律(45)，则系统有以下性质:

i) 系统中所有信号有界，且

ii) 保证迭代过程中，-bi1＜εi，k＜bi2成立，同时系统状态有界约束始终满足.

证i) 变量有界性和系统收敛性.

选择第k次的障碍Lyapunov泛函为

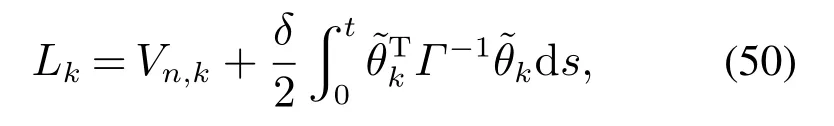
连续2次迭代周期的差分为

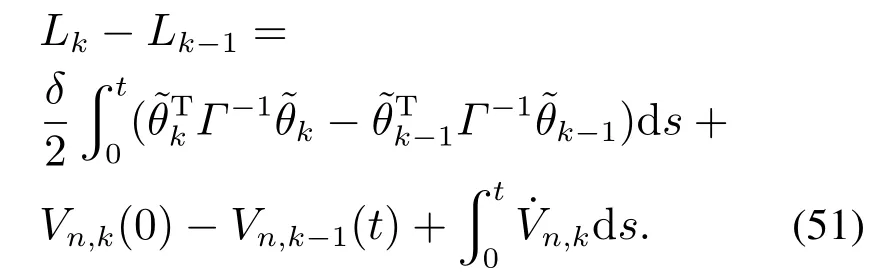
将式(48)代入式(51)，得

令t=T，重复式(52)k次，并结合Lk(T)的非负性，得

因为L1(T)有界，则由于闭环系统中的所有参数保持有界，可以得出是有界的.由于其导数一致有界，在区间[0，T]上利用Barbalat引理，可知=0.

ii) 系统状态的有界约束.

由定理2中第i)部分证明可知，在各次迭代过程中，有-bi1＜εi，k＜bi2.现在证明本定理中的状态有界约束，步骤类似于定理1中第ii)部分的证明过程.由于x1，k=可得到其中:由于xi，k=同样可以证明，其中:证毕.

可以看出，运用本节构造的二次分式型非对称BLF函数，通过将εi，k囿于预设的界内，间接地实现对状态的约束.

综上，本文通过引入期望误差轨迹来解决迭代学习系统的初值问题，且期望误差轨迹的设计方法简单.构造了二次分式型BLF函数的两种典型形式来分别设计控制器.由定理1-2的分析和证明部分可以看出，跟踪误差在迭代过程中囿于预设的界内，从而实现对系统状态的有界约束.

4 数值仿真

为验证所提算法的有效性，考虑如下二阶严格反馈非线性系统:

取i=1，2，当t∈[0，t1]时，

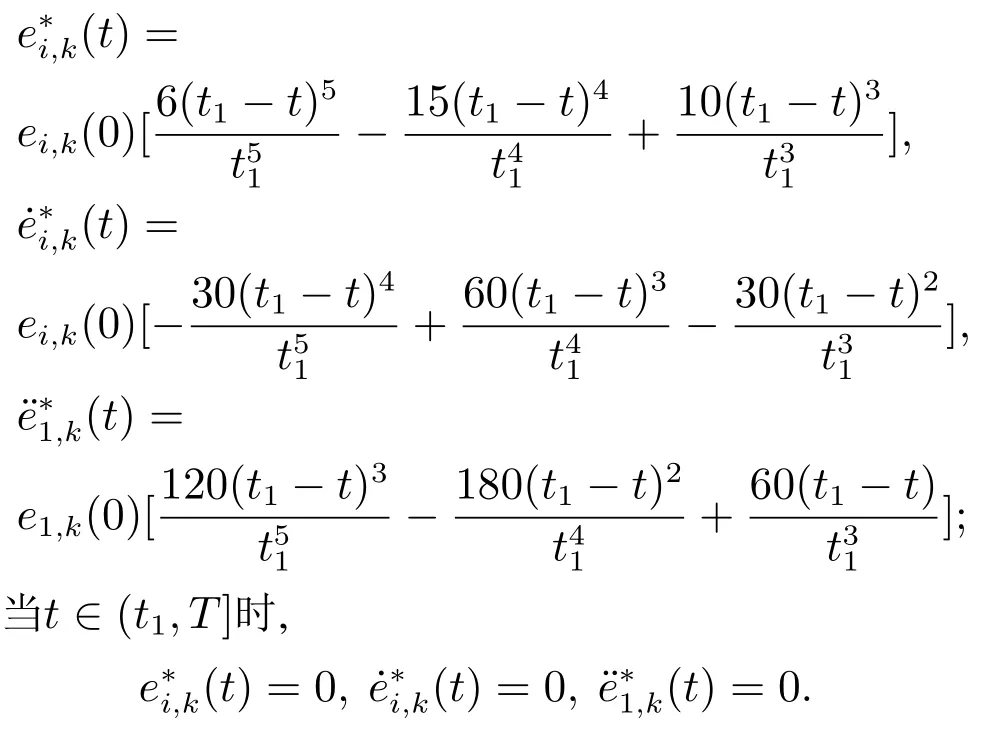
根据对称BLF函数和非对称BLF函数这两种情形，分别进行仿真:

1) 对称BLF函数情形.

设定|x1，k|＜1.61和|x2，k|＜6.78以及b1=0.01，b2=0.5.采用控制律(23)以及积分学习律(24)，迭代20次后，仿真结果如图1-4所示.

图1 情形1下的x1(t)及其期望轨迹r1(t)Fig.1 x1(t)and its desired trajectory r1(t)in Case 1

图2 情形1下的控制输入Fig.2 Control input in Case 1

图3 情形1下的e1(t)和期望误差轨迹Fig.3 e1(t)and the desired error trajectory in Case 1

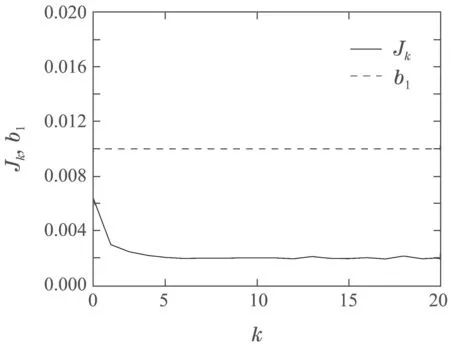
图4 情形1下的误差性能指标JkFig.4 Error performance index Jk in Case 1

2) 非对称BLF函数情形.

设定

采用控制律(44)以及微分-差分学习律(45)，迭代20次后，仿真结果如图5-8所示.

图5 情形2下的x1(t)及其期望轨迹r1(t)Fig.5 x1(t)and its desired trajectory r1(t)in Case 2

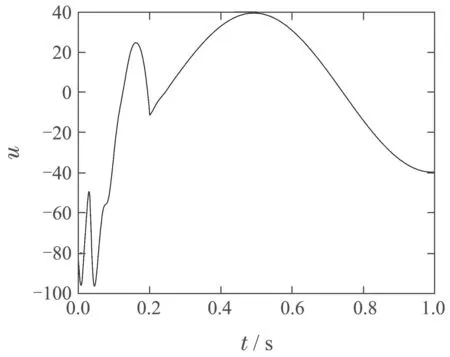
图6 情形2下的控制输入Fig.6 Control input in Case 2

图7 情形2下的e1(t)和期望误差轨迹Fig.7 e1(t)and the desired error trajectory in Case 2

图8 情形2下的误差性能指标JkFig.8 Error performance index Jk in Case 2

图1和图5表明，由t=0.2起系统输出完全跟踪上参考信号;图3和图7表明，本文提出的两种控制方案都能够在任意初值下，使得状态误差在整个作业区间上实现对期望误差轨迹的精确跟踪;图4和图8可以看出在迭代过程中，|ε1，k(t)|，t∈[0，T]被约束于[0，b1]区间内.

为了比较，采用无约束学习控制

以及积分学习律

进行仿真，期望误差轨迹的构造及各参数值选取同前.图9是控制律(55)作用下，|ε1，k|随迭代次数变化的情况.可以看出，无约束学习控制策略不能保证Jk≤b1.

图9 无约束学习控制下的Jk收敛过程Fig.9 The convergence performance of Jk without BLF

5 结论

本文给出一类严格反馈非线性系统的学习控制算法.文中构造两种形式简单的二次分式型BLF函数，并结合反推技术分别进行控制器设计，保证系统状态在各次迭代中受到约束.为了解决初值问题，引入期望误差轨迹，实现系统输出在预指定区间上精确跟踪参考信号.