陈 强，余歆祺

(浙江工业大学信息工程学院，浙江杭州 310023)

1 引言

重复控制与迭代学习控制同属学习控制，旨在利用上一周期或上一次迭代的运行数据来修正当前控制输入，进而改善系统的控制性能.不同的是，前者适用于连续、周期运行的系统，而后者适用于在有限时间区间上重复运行的对象.重复控制可以有效地跟踪周期性期望轨迹或抑制周期性扰动，且工程实现时不需要完全依赖系统参数，因此易于工程应用.

经典重复控制主要基于内模原理，在频域内进行控制器设计[1-2].文献[3]针对带有周期扰动的时延系统设计了一种重复控制器，并设计干扰观测器补偿外部周期干扰的影响.文献[4]针对非严格重复逆变器系统设计了一种自抗扰学习控制方法，可以良好地抑制短时扰动造成的输出电压周期波动，提高系统稳定性.文献[5-6]针对一类时变不确定系统，基于2维系统稳定性理论提出一种鲁棒重复控制器，保证系统的鲁棒性与稳态跟踪精度.文献[7-8]在恒压恒频脉冲宽度调制(pulse width modulation，PWM)逆变器中应用重复控制技术设计控制器，有效提高了系统跟踪精度并抑制了谐波.此外，在有源电力滤波器[9]，伺服系统[10]等场合，重复控制也得到了广泛应用.

近年来，基于Lyapunov方法的重复学习控制引起了广泛关注[11-13].重复学习控制器设计通常需要处理两类系统不确定性，即参数不确定性与非参数不确定性.其中，处理参数不确定性时，系统需满足可参数化条件，重复学习控制主要针对未知参数进行学习[14-15].然而，实际系统中存在的非参数不确定性，例如伺服电机、机器人系统中的状态相关负载转矩以及各种未建模动态等，使得系统的可参数化条件难以满足[16].因此，有必要研究非参数不确定系统的重复学习控制方法.文献[17]针对一类非参数不确定系统，设计重复学习控制器用于解决输出跟踪问题，同时引入两个状态观测器用于估计系统和参考状态信息.文献[18]针对一类期望轨迹与扰动之间无公共周期的非参数不确定系统，提出了一种双周期重复学习控制方法.文献[19]针对一类满足Lipschitz条件的非参数不确定系统设计重复学习控制器，但重复学习律的设计中并未考虑对估计值进行限幅.文献[20]针对电流反馈永磁步进电机提出一种重复学习控制方法，并通过部分限幅学习律保证估计值的有界性.然而，由于学习律中含有未限幅项，因此不能保证将估计值限制在指定的界内.针对这一问题，文献[21]提出一种全限幅学习律，但目前基于全限幅学习律的重复学习控制文献相对较少.此外，文献[18-20]处理系统不确定性时，需要已知不确定性的界，然而实际中系统不确定性的界难以直接获得.

基于以上讨论，本文针对一类非参数不确定系统，基于Lyapunov方法提出一种全限幅自适应重复学习控制方法，实现对周期性期望轨迹的高精度跟踪.本文主要工作包括:1)利用期望轨迹的周期特性，构造周期性期望控制输入设计自适应重复学习控制器，提高系统的稳态跟踪精度，且无需已知非参数不确定性的界;2)设计全限幅学习律对未知周期性期望控制输入进行估计，与已有的部分限幅学习律相比，该学习律可保证估计值被限制在指定的界内;3)通过构造完全平方式消除部分误差相关项，控制器设计中避免了使用符号函数，从而保证控制信号连续以及抑制控制器抖振问题.

2 问题描述

考虑如下非参数不确定系统[22]:

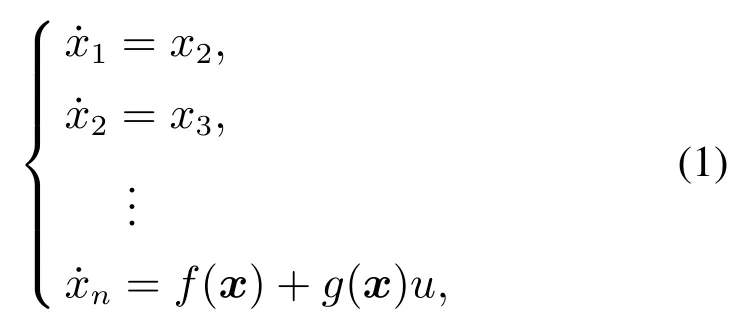
其中:x=[x1x2… xn]T∈Rn表示系统状态;u∈R表示控制输入;f(x)和g(x)均为未知有界非线性函数，其中f(x)表示系统中的非参数不确定性，g(x)表示与状态相关的控制增益.

假设1g(x)为恒正或恒负的有界函数，即存在正常数gm和gM，使得对∀x∈Rn，有gm≤|g(x)|≤gM成立.不失一般性，本文假设g(x)＞0.

假设2f(x)和g(x)均满足Lipschitz 条件，即对∀z1，z2∈Rn，有|f(z1)-f(z2)|≤lf0‖z1-z2‖和|g(z1)-g(z2)|≤lg0‖z1-z2‖成立，其中:‖·‖表示向量的2-范数，lf0，lg0＞0为未知Lipschitz系数.

本文考虑周期为T的有界期望轨迹xr=[x1rx2r… xnr]T，即xr(t)=xr(t-T)，可构造期望控制输入

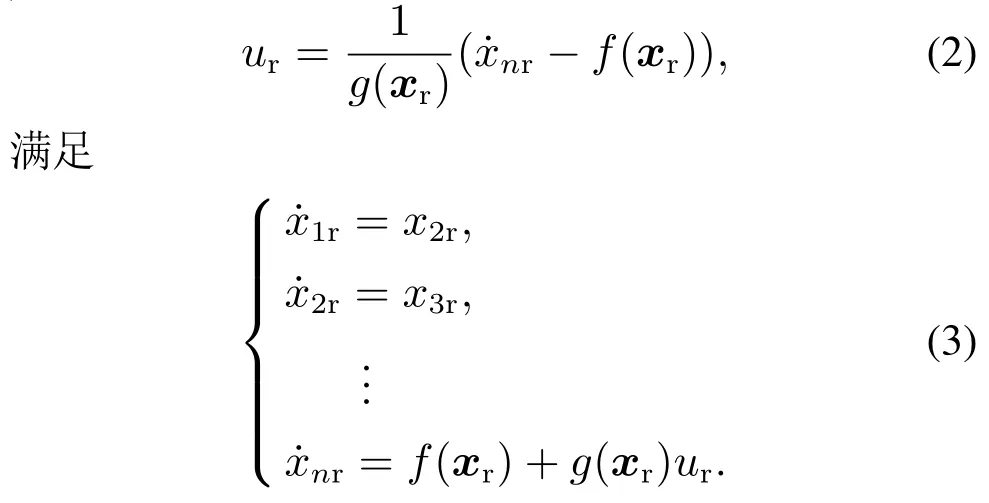
由xr的周期性可知，ur同样为周期为T的周期信号，即ur(t)=ur(t-T).

本文控制目标为，根据期望轨迹xr和期望控制输入ur的周期特性，设计自适应重复学习控制器u，实现系统状态x对期望轨迹xr的高精度跟踪.

3 自适应重复学习控制

3.1 误差动态

定义跟踪误差

根据式(1)，跟踪误差的导数满足

则式(5)可写为

定义向量a=[a1a2… an]，则式(8)可表示为

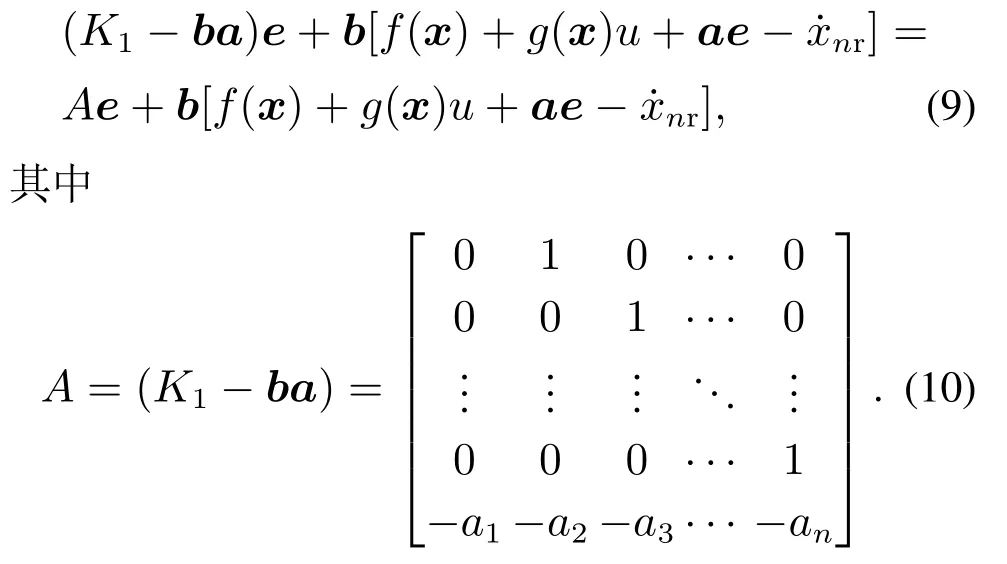
选择向量a=[a1a2… an]，使得特征多项式D(s)=sn+ansn-1+…+a2s+a1为Hurwitz多项式，保证矩阵A渐近稳定，从而对任意对称正定矩阵Q∈Rn×n，存在唯一的对称正定矩阵P∈Rn×n使得以下Lyapunov方程成立:

令λQ为矩阵Q的最小特征值，则对任意向量v∈Rn，有-vTQv≤-λQ‖v‖2成立.

重复学习控制主要用于处理系统中的周期不确定性，然而在误差动态(9)中，系统不确定性并没有表现出周期特性，因此难以直接基于式(9)设计重复学习控制器.因此，本文利用周期性期望控制输入ur改写式(9).将代入式(9)得

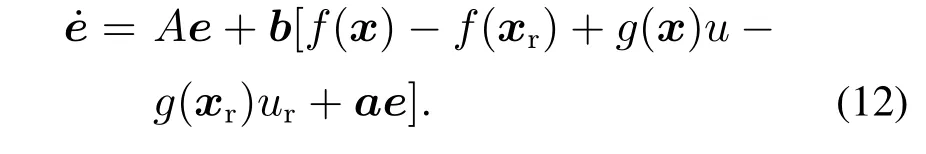
3.2 自适应重复学习控制设计

构造如下Lyapunov函数:

对V 求导可得

将式(12)代入式(14)有

其中α=bTPe.

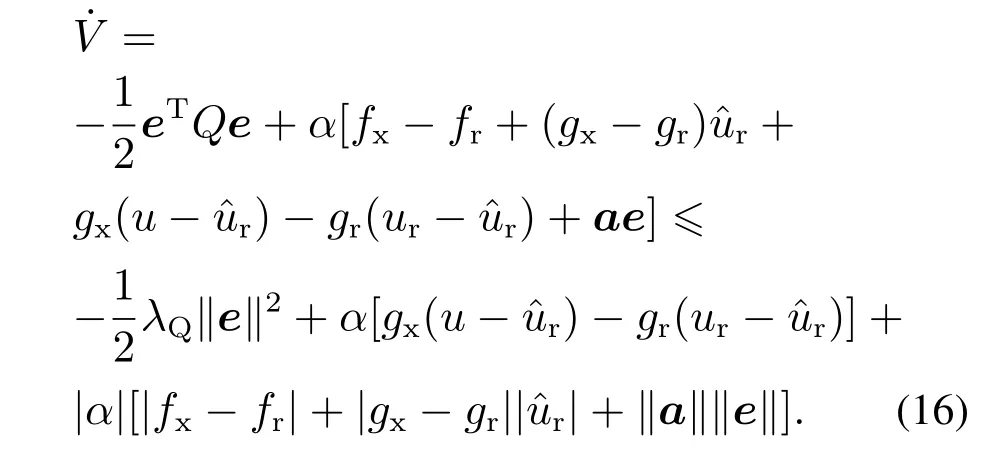
根据假设2，有|fx-fr|≤lf0‖e‖和|gx-gr|≤lg0‖e‖，代入式(16)有

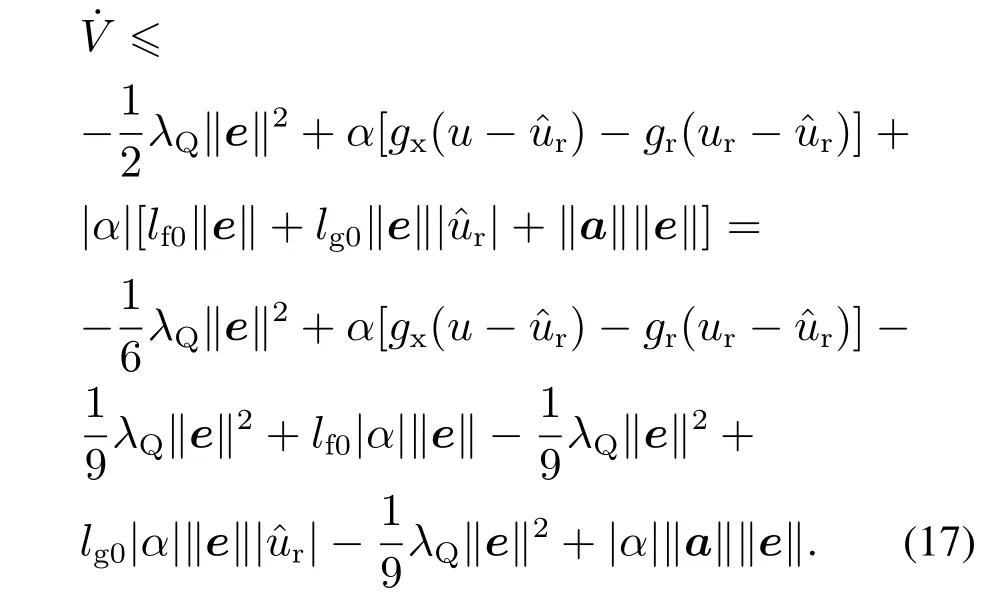
构造如下完全平方式:

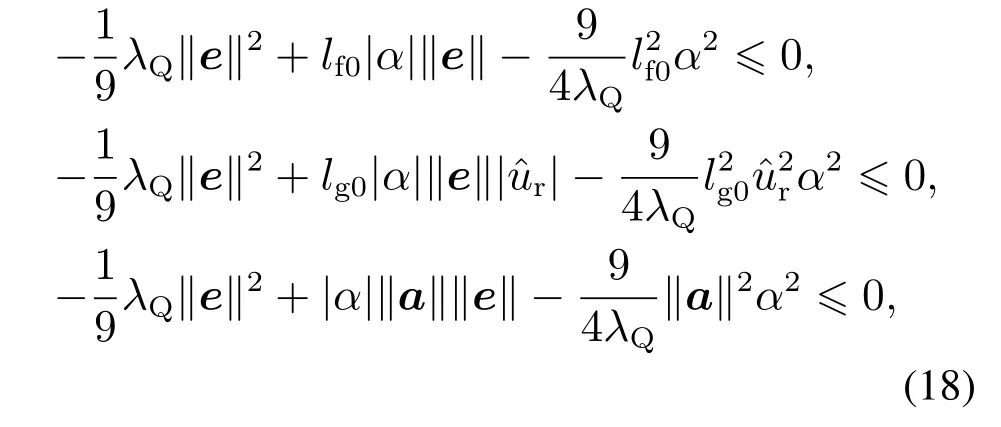
则式(17)可改写为

根据式(19)，设计自适应重复学习控制器u，表达式为

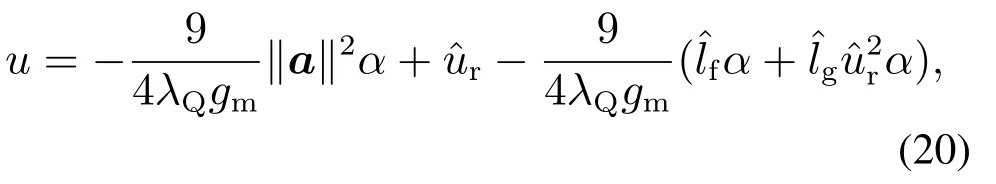
考虑未知期望控制输入ur的周期性和有界性，设计如下全限幅重复学习律用于更新

其中:μ0为学习增益，sat(·)为饱和函数，对任一标量a有

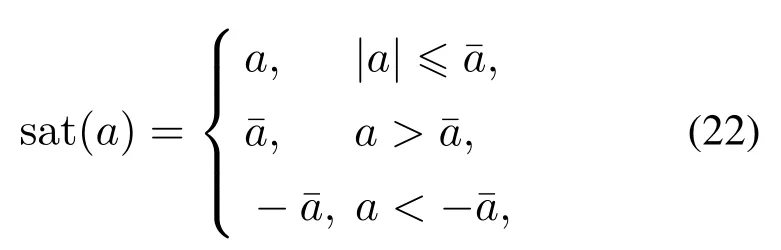
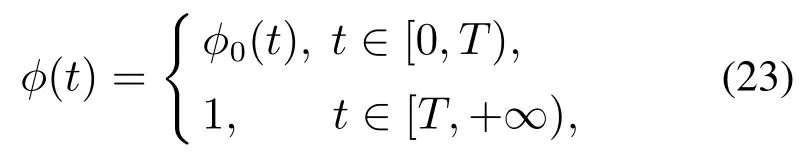
其中φ0(t)在t∈[0，T)上单调递增，且满足φ0(0)=0.

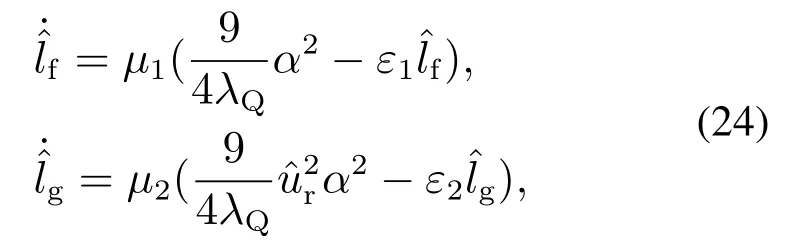
其中μ1，μ2，ε1，ε2为正常数.选择0，由式(24)可以得出

将式(20)代入式(19)可得

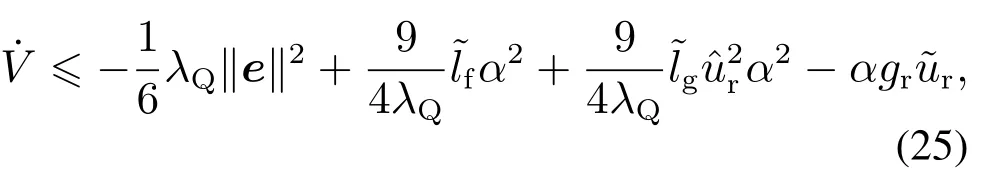
注1通过构造完全平方式(18)消除式(17)中的控制器(20)避免了使用符号函数，从而削弱控制器的抖振现象.

注2本文所设计的全限幅学习律(21)有别于常用的部分限幅学习律，即根据α的表达式，只要ei，i=1，2，…，n有界，部分限幅学习律同样可以保证有界.然而与全限幅学习律相比，部分限幅学习律由于含有未限幅项因此难以保证将限制在指定的界内.

注3式(21)中，函数φ(t)用以保证在t=iT，i=0，1，2，3，…处的连续性[14]，其中φ0(t)可选为线性或非线性形式.为便于实现，本文φ0(t)简单取为线性函数

注4根据误差动态(9)，可直接设计如下自适应鲁棒控制器(adaptive robust control，ARC)

注5本文所设计的全限幅学习律也可以用于定常参数lf，lg的估计.然而在实际工程应用中，额外的重复学习律需要使用更多的内存空间，导致硬件成本的上升.为此，本文设计自适应更新律来估计未知参数lf，lg，在不影响控制性能的前提下，更利于实际应用.

4 收敛性分析

引理1[13]给定标量a，b，假设|a|≤¯b，其中¯b为b的限幅值，有如下不等式成立:

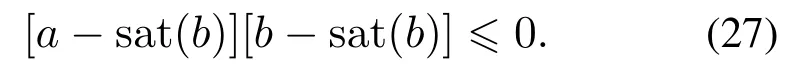
定理1给定周期性期望轨迹xr，设计重复学习控制器(20)，全限幅重复学习律(21)以及自适应更新律(24)，则系统(1)的跟踪误差2-范数收敛至原点附近的邻域内.

证构造如下类Lyapunov函数:

对式(28)求导，可得

考虑xr和ur的周期特性，即xr(t)=xr(t-T)，ur(t)=ur(t-T)，式(29)可写为

由于(a-b)2-(a-c)2=(2a-b-c)(b-c)，因此式(30)可改写为

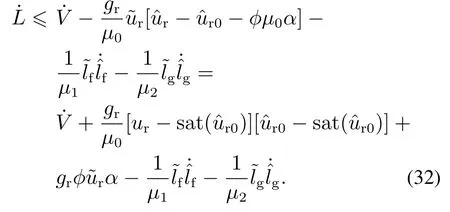
根据引理1，有不等式[ur-sat(ˆur0)][ˆur0-sat(ˆur0)]≤0成立，从而式(32)可化简为

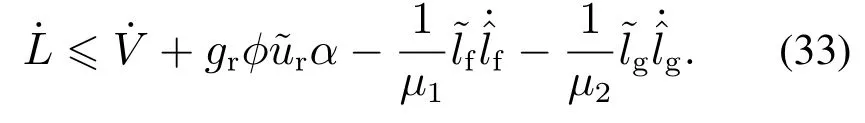
将式(25)代入式(33)可得

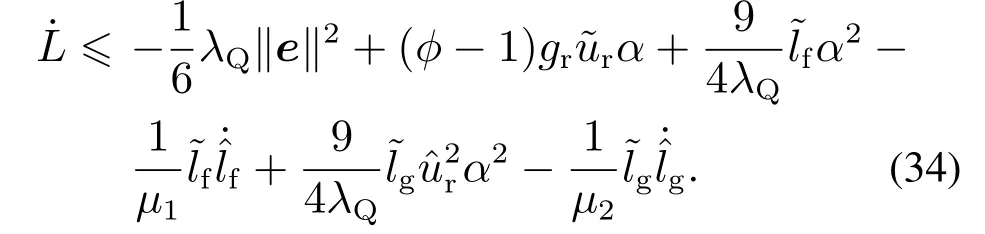
将自适应更新律(24)代入式(34)可得

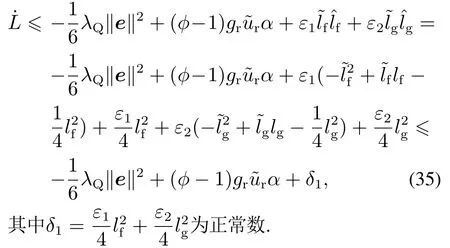
根据函数φ(t)的定义(23)，分别在t∈[0，T)以及t∈[T，+∞)两个区间上分析‖e‖的收敛性.

当t∈[0，T)时，有

当t∈[T，∞)时，由于φ ≡1，由式(35)可得

由式(38)可知，选择较小的δ1或具有较大λQ的矩阵Q，可保证‖e‖最终收敛到原点附近的邻域内，且该邻域随着δ1的减小或λQ增加而减小.证毕.

注6根据δ1的表达式可以看出，减小参数ε1和ε2可保证较小的δ1.然而由式(24)可知，过小的ε1和ε2会降低和的收敛速度.此外，由控制器(20)可以看出，过小的λQ会使得控制器增益过低，从而影响跟踪误差的收敛速度.

5 仿真结果及分析

本节通过永磁步进电机系统与三阶非线性系统两个仿真实例验证所提自适应重复学习控制(adaptive repetitive learning control，ARLC)方法的有效性.

例1在d-q坐标系下，电流反馈永磁步进电机模型表达式为[20]

其中:x1，x2分别表示转子位置、速度，J表示转动惯量，Nr表示极对数，D表示粘滞摩擦系数，TL(·)表示负载转矩，if表示永磁体等效电流，u为q轴输入电流，表示齿槽转矩，cos[(1-i)Nrx1]表示非正弦气隙磁链分布，仿真中取j=4.电机模型具体参数如表1所示.

表1 永磁步进电机模型参数Table 1 Model parameters of the permanent magnet stepper motor

对比式(1)与式(39)，可得控制增益gx表达式为

由表1可知，系统中Lmi，i=2，3，4远小于Lm1，因此存在正常数gm，满足gx≥gm.

周期性期望轨迹设为x1r=sin(0.5πt)，其中周期T=4 s.矩阵A，Q分别取为

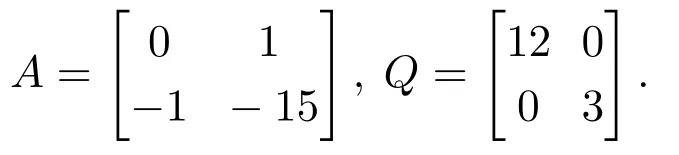
通过求解Lyapunov方程(11)得

其他控制参数设置为gm=2.8，μ0=240，μ1=0.2，μ2=80，ε1=1×10-4，ε2=1×10-5.系统初值设置为x1(0)=0.4，x2(0)=0.

仿真结果如图1-5所示，其中图1和图2分别描述了系统状态跟踪轨迹与跟踪误差的2-范数收敛轨迹.由图1和图2可以看出，本文所提的自适应重复学习控制方法对周期期望轨迹具有良好的跟踪效果，且随着系统的周期运行，跟踪误差2-范数收敛至原点附近.图3给出了期望控制输入ur的估计值及其估计误差.由图3可知，本文所设计的全限幅学习律(21)可以较准确地估计期望控制输入ur.图4给出了系统的控制输入信号，对比图3和图4可见，系统控制输入u的波形基本与期望控制输入ur波形保持一致.需要说明的是，所用的永磁步进电机系统(39)包含了大量的齿槽转矩与非正弦气隙磁链分布，因此期望控制输入ur本身含有大量的谐波成分，由于所提ARLC方法可以较准确地估计ur，因此u的曲线并不光滑，这与理论分析中保证控制信号连续的结论并不矛盾.图5给出了未知常数lf，lg的估计.由图1-5可以看出，本文所提的自适应重复学习控制方法能够实现对期望控制输入的准确估计以及对周期期望轨迹的高精度跟踪.

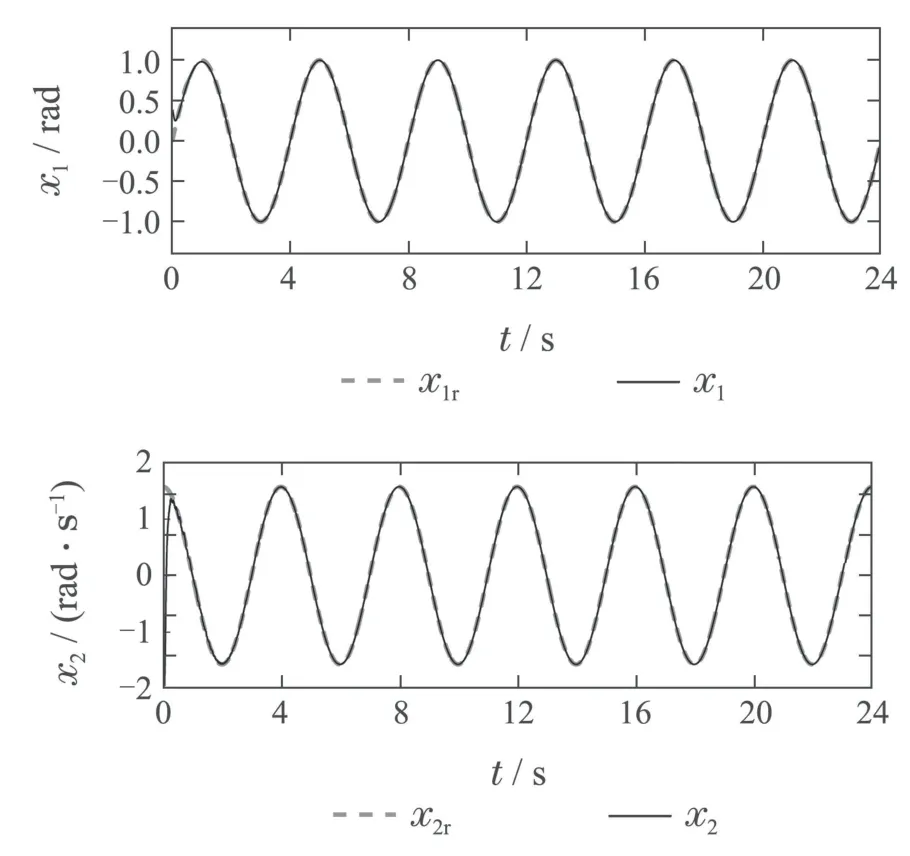
图1 状态跟踪轨迹Fig.1 States tracking trajectories

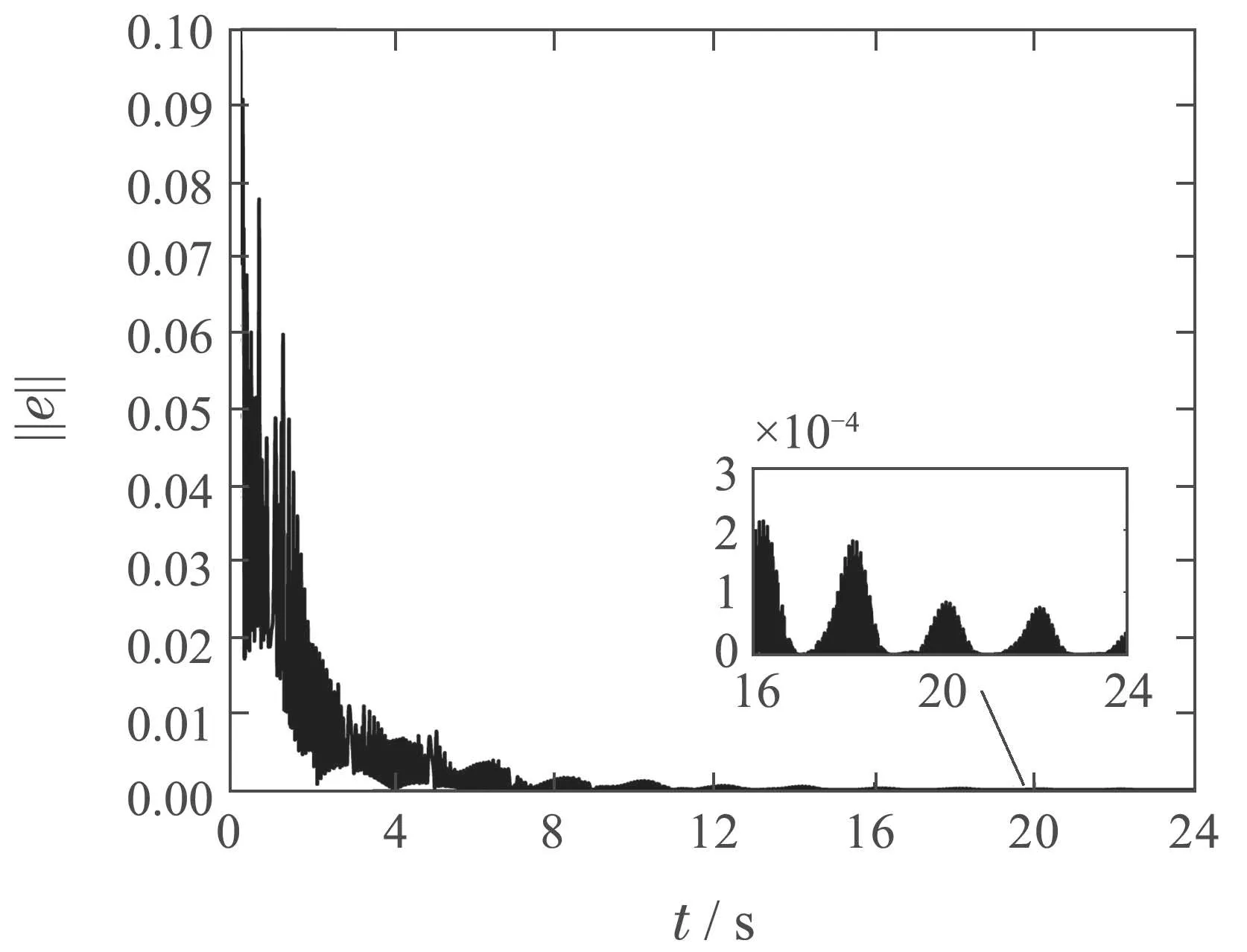
图2 跟踪误差2-范数Fig.2 2-norm of the tracking error

图3 期望控制输入的估计及其估计误差Fig.3 Estimate of the desired control input and the estimation error

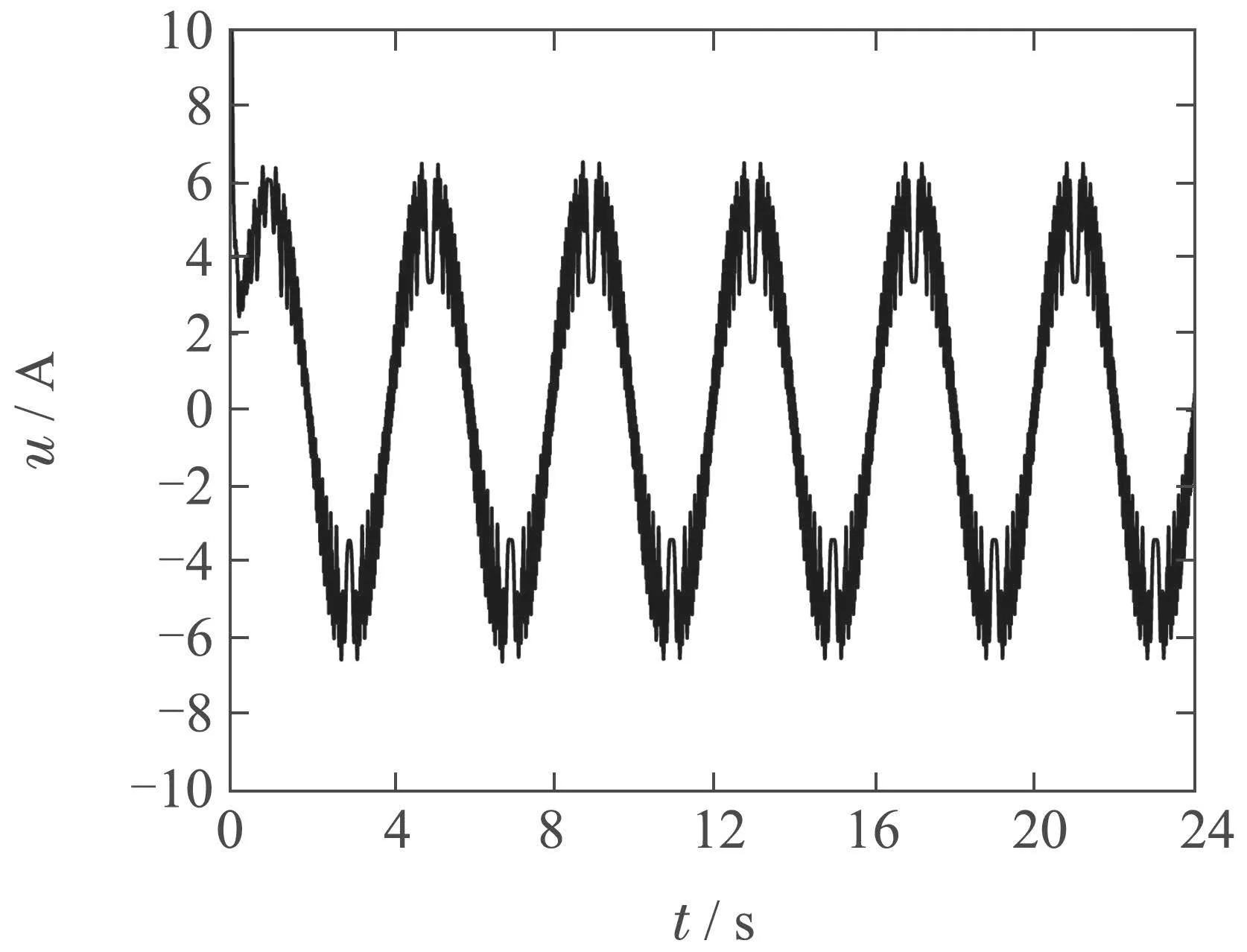
图4 控制输入Fig.4 Control input

图5 未知参数lf，lg的估计Fig.5 Estimates of the unknown parameters lf and lg

例2考虑如下三阶非线性系统:

期望轨迹设为x1r=sin(0.5πt)，周期为T=4 s，矩阵A，Q分别设为

通过求解Lyapunov方程(11)得

其他控制参数设置为gm=0.6，μ0=240，μ1=0.2，μ2=80，ε1=1×10-4，ε2=1×10-5.

为显示本文所提ARLC方法的优越性，进一步给出与自适应鲁棒控制(adaptive robust control，ARC)方法以及自适应神经网络控制(adaptive neural-network control，ANNC)方法的对比[23].其中ARC控制器形式由式(26)给出，且ˆρ的自适应更新律设计为

其中参数设置为μρ=2，ερ=7×10-2.ARC控制器(26)中gm同样设置为0.6，矩阵A，Q，P 的取值同式(42)-(43)，即与ARLC控制器相同.

ANNC控制器由文献[23]给出，具体形式如下:

虚拟控制器α1，α2和控制器u定义为

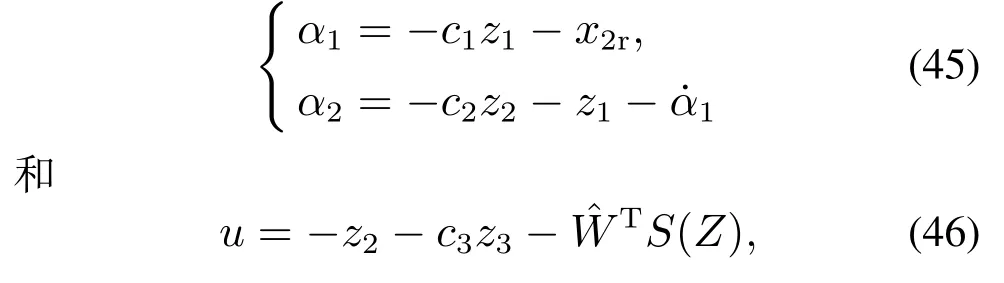
其中:c1，c2，c3为正常数;z1，z2和z3为误差变量，表达式为

S(Z)=[s1(Z) s2(Z) … sl(Z)]T，Z∈Rq为q维输入向量，l 表示神经网络节点个数.si(Z)，i=1，2，…，l取为高斯函数，表达式为

其中:μi=[μi1μi2… μiq]为聚类中心，ηi为高斯函数宽度.此外，式(46)中为神经网络权值向量的估计值，其更新律为

其中:σ为正参数，Γ为增益矩阵.

本仿真实例中，c1，c2和c3的取值根据式(43)的最后一行在一定范围内进行调节，选取跟踪效果较好的一组取值为c1=20，c2=25，c3=30.输入向量Z=神经网络节点数l=100;聚类中心μi(i=1，2，…，l)分布于[-3，3]×[-3，3]×[-3，3]×[-3，3]×[-3，3]×[-3，3]×[-3，3];高斯函数宽度取为ηi=10，i=1，2，…，l;增益矩阵Γ=2×I6，其中I6为单位矩阵;正参数σ=0.5.

仿真对比结果如图6-10所示.图6和图7给出了ARLC与ARC以及ANNC的跟踪性能对比.由图6和图7可见，在ARC或ANNC控制下系统稳态时仍存在一定的周期性跟踪误差;而在ARLC控制下，系统周期性跟踪误差随着系统运行被逐渐消除.因此，本文所提ARLC方法具有更高的周期轨迹跟踪精度.图8给出了ARLC与ARC以及ANNC的控制输入对比，由图8可以看出，ARC方法存在明显的抖振现象，而ARLC方法和ANNC方法由于在控制设计时避免了使用符号函数，有效抑制了控制器抖振问题.图9给出了期望控制输入的估计及其估计误差可以看出本文所设计的学习律(21)可实现对期望控制输入的准确估计.图10给出了未知常数lf，lg的估计.

图6 ARLC与ARC以及ANNC的跟踪轨迹对比Fig.6 Comparison of tracking trajectories among ARLC，ARC and ANNC

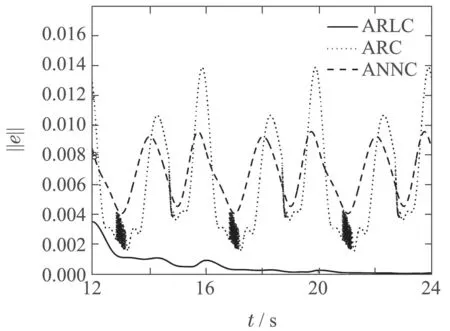
图7 ARLC与ARC以及ANNC跟踪误差2-范数对比Fig.7 Comparison of 2-norm of tracking error among ARLC，ARC and ANNC

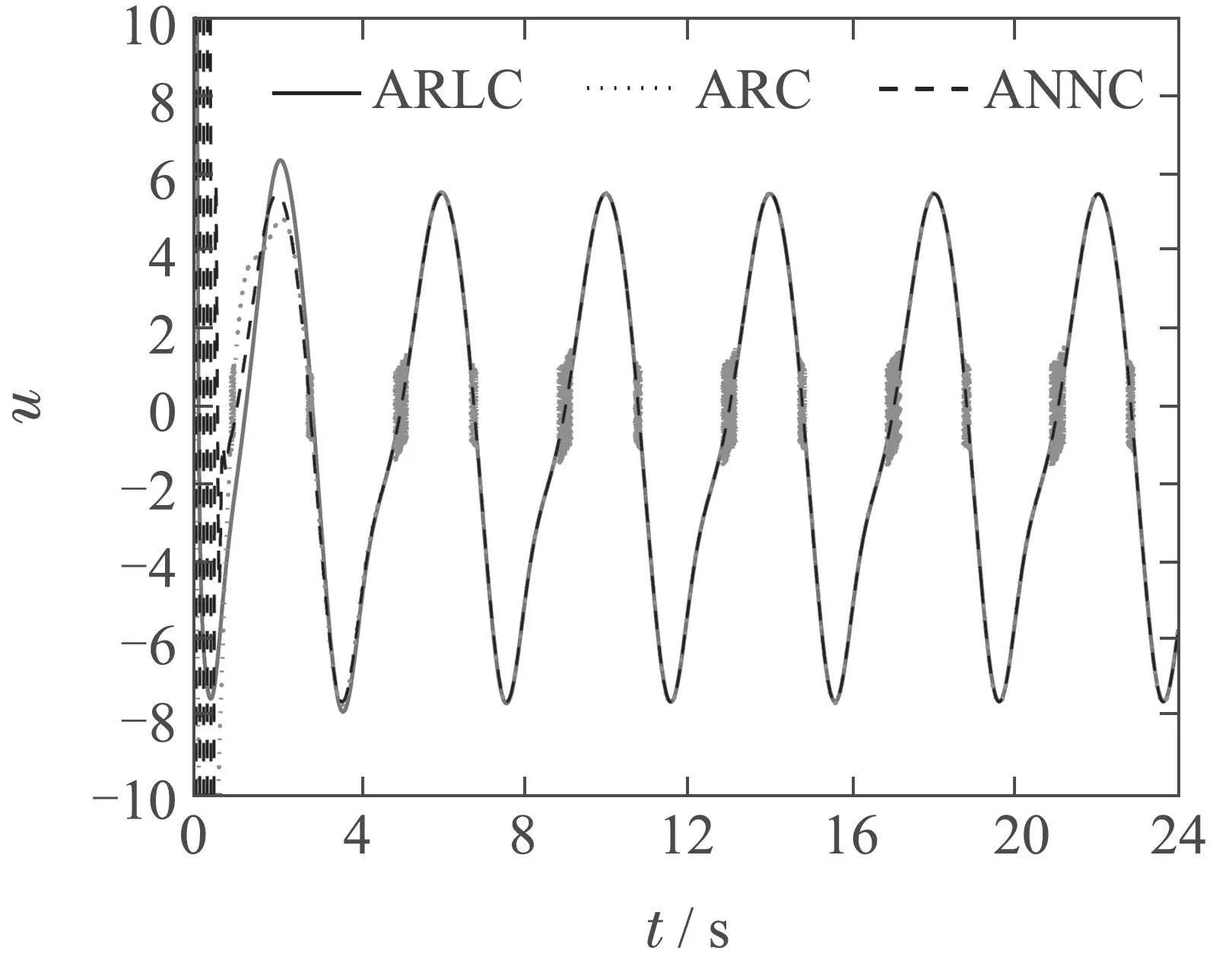
图8 ARLC与ARC以及ANNC控制输入对比Fig.8 Comparison of control inputs among ARLC，ARC and ANNC

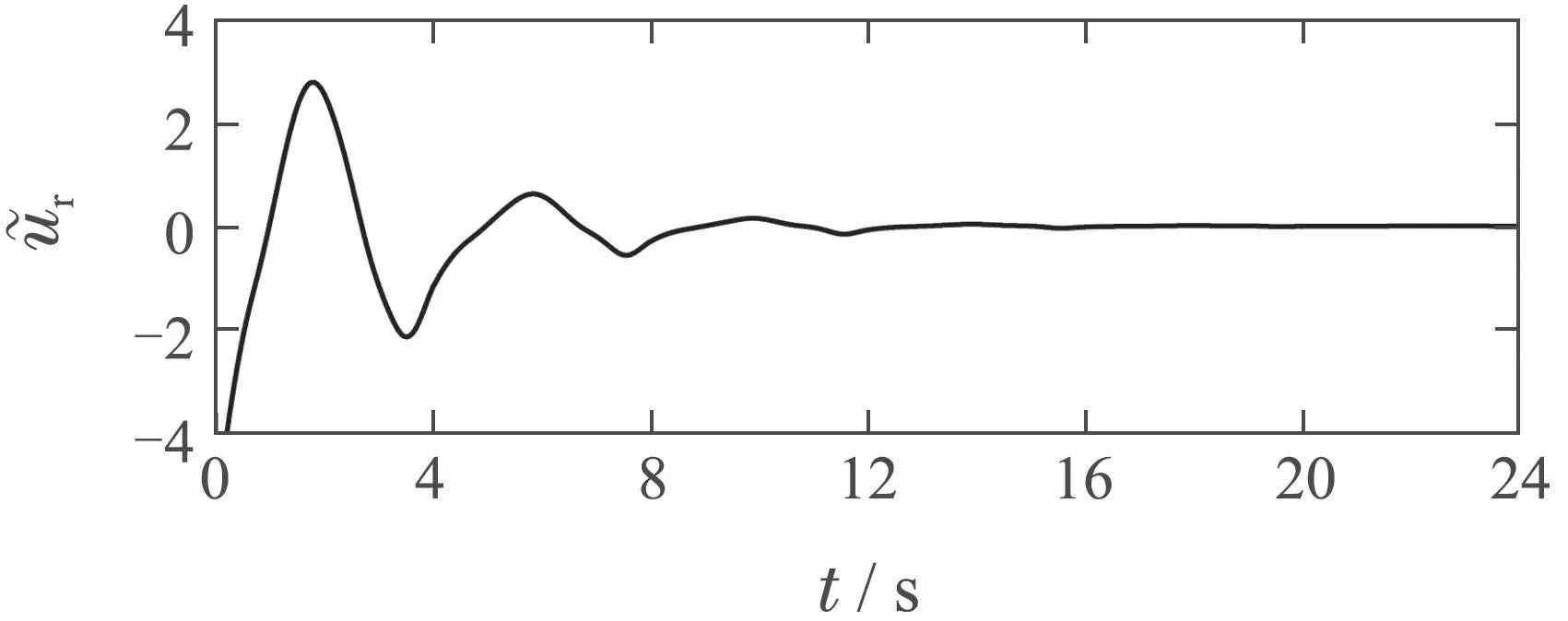
图9 期望控制输入的估计及其估计误差Fig.9 Estimate of the desired control input and the estimation error

图10 未知参数lf，lg的估计Fig.10 Estimates of the unknown parameters lf and lg

由图6-10可以看出，本文所提ARLC方法能够实现对周期轨迹的高精度跟踪以及对期望控制输入的准确估计.在消除系统周期性跟踪误差和提高系统跟踪精度的同时，能够有效抑制控制器抖振问题.

6 结论

本文针对一类非参数不确定系统，基于Lyapunov方法设计自适应重复学习控制器，实现系统对周期性期望轨迹的高精度跟踪.利用期望轨迹的周期特性，构造周期性期望控制输入，并设计全限幅学习律对其估计，保证估计值被限制在指定的界内.通过构造完全平方式消除部分误差相关项，控制器设计中可避免使用符号函数，从而保证控制信号连续.此外，对非参数不确定性界的平方设计自适应估计律，减少控制器对系统模型信息的依赖.仿真对比验证了本文所提方法的有效性.