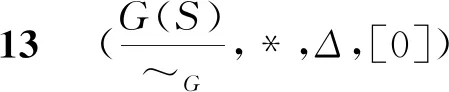邓方安

(陕西理工大学 数学与计算机科学学院，陕西 汉中 723001)

1966年，Imai等[1]和Iseki[2]提出了BCI-代数和BCK-代数的概念.众所周知，BCK-代数是BCI-代数的真子类，许多学者推广了这两类代数，引入和研究了不同类型的新代数.1983年，Hu等[3]推广了BCI-代数，引入了BCH-代数，并研究了它的性质.后来，Ahn等[4]又推广了BCH-代数，提出了一类新的代数，即BH-代数.2001年，Neggers等[5]提出了一个新的代数系统，称为Q-代数，并推广了BCI-代数和BCK-代数中的一些定理.2002年，Neggers等[6]引入了B-代数，并得出了B-代数的一些性质.2007年，Walendziak[7]提出了BF-代数，它是B-代数的推广.另外，Kim等[8]还引入了BG-代数，该代数是B-代数的推广.在此基础上，Bandaru[9]推广了BCK/BCI/BCH/Q/QS/BM代数，提出了BRK-代数的概念. 2017年，Venkateswarlu等[10]对BRK-代数进行了深入研究，定义了弱正蕴涵BRK-代数以及一些性质.

1996年，作者提出了N(2,2,0)代数概念，并系统研究了该代数的性质，得到了系列研究成果[10-11].论文将研究N(2，2,0)代数与BRK-代数的关系，并进一步刻画N(2，2,0)代数的性质.

1 预备知识

为研究方便，先引入有关BCI/BCH/BCK/Q-代数的定义.

定义1[1]BCI-代数(X,*,0)满足以下条件：∀x,y,z∈X，有

(B1) (x*y)*(x*z)≤(z*y);

(B2)x*(x*y)≤y;

(B3)x≤x;

(B4)x≤y,y≤x⟹x=y;

(B5)x*y=0,x≤y,x≤0⟹x=0.

注：如果将(B5)替换为(B6)，即0≤x，则该代数称为BCK代数.由文献[1]知，每个BCK-代数都是一个BCI-代数，反之不然.

定义2[2]一个BCH-代数(X,*,0)是满足条件(B3),(B4)，(B7)，(B7)即(x*y)*z=(x*z)*y的代数.

注：每个BCI-代数都是一个BCH-代数，反之则不然.

定义3[5]一个Q-代数(X,*,0)是满足(B3),(B7),(B8)，(B8)即x*0=x的代数.如果一个Q-代数满足(B9)，即(x*y)*(x*z)=z*y，则称Q-代数为QS-代数.

注：每个BCH-代数都是一个Q-代数，反之则不然.

定义4[6]一个B-代数(X,*,0)是满足(B3),(B8),(B10)，(B10)即(x*y)*z=x*(z*(0*y))，∀x,y,z∈X的代数.如果对于任意a,b∈X,a*(0*b)=b*(0*a)，B-代数是非交换的，则B-代数和Q-代数是不同的概念.

定义5[7]一个BF-代数(X,*,0)是满足(B3),(B8),(B11)，(B11)即0*(x*y)=y*x的代数.

注：每一个B-代数都是BF-代数，反之则不然.

定义6[9]一个BM-代数(X,*,0)是满足(B8),(B12)，(B12)即(x*y)*(x*z)=z*y的代数.

定义7[4]一个BH-代数(X,*,0)是满足(B3),(B4),(B8)的代数.

定义8[8]一个BG-代数(X,*,0)是满足(B3),(B8),(BG)，(BG)即(x*y)*(0*y)=x的代数.

2 BRK-代数及基本性质

下面给出BRK-代数定义，并研究它与其他几种代数之间的关系.

定义9[9]定义X为非空集合，常数为0，如果满足二元运算(*)

(B8)x*0=x;

(B13) (x*y)*x=0*y,这里x,y∈X.

则称(X,*,0)构成的代数为BRK-代数.

例1定义非空集合A=R-{n}，0≠n∈Z+，满足二元运算“*”

显然，(A,*,0)为BRK-代数.

例2定义非空集合A={0,1,2}，满足如表1所示的二元运算“*”.

表1 集合A满足的二元运算

显然代数(A,*,0)满足(B8)，可以验证满足(B13)，即(x*y)*x=0*y，有

当y为0时，(x*0)*x=0*0=0；

当y为1时，(x*1)*x=0*1=2；

当y为2时，(x*2)*x=0*2=2.

故∀x,y∈A，有(x*y)*x=0*y成立，则代数(A,*,0)为BRK-代数.

定理1[9]如果(X,*,0)是一个BRK-代数，那么对任意x,y∈A，满足：

(1)x*x=0；

(2)x*y=0⟹0*x=0*y.

定理2[9]在每个BRK-代数(X,*,0)中，∀x,y∈X，满足

0*(x*y)=(0*x)*(0*y),x,y∈X.

定理3[9]每个满足x*(x*y)=x*y,x,y∈X的BRK-代数是一个平凡的BRK代数.

定理4[9]每个满足(x*y)*(x*z)=z*y,x,y,z∈X的BRK-代数是一个BCI-代数.

定理5[9]每一个非交换的B-代数是一个BRK-代数.

定理6[9]设(X,*,0)为BRK-代数，对任意的x,y∈X，则下面的条件成立：

(1)设(x*y)*[0*(0*y)]=(x*y)*y,则0*[0*(0*y)]=0*y；

(2) (x*y)*(0*y)=(x*y)*y⟹0*(0*y)=0*y；

(3)x*(y*x)=x*[0*(x*y)]⟹0*(y*x)=0*[0*(x*y)].

3 N(2,2,0)代数与BRK-代数

定义10[11]设S是含常元0的集合，在S中定义两个二元运算*和Δ，∀x,y,z∈S，若满足以下公理：

(F1)x*(yΔz)=z∈(x*y)；

(F2) (xΔy)*z=y*(x*z)；

(F3) 0*x=x.

则称(S,*,Δ,0)是一个N(2,2,0)代数.

定理7[11]在N(2,2,0)代数(S,*,Δ,0)中，∀x,y,z，恒有下列等式成立：

(F4)x*y=yΔx；

(F5) (x*y)*z=x*(y*z),(xΔy)Δz=xΔ(yΔz)；

(F6)x*(y*z)=y*(x*z),(xΔy)Δz=(xΔz)Δy．

推论1[11]若(S,*,Δ,0)是一个N(2,2,0)代数，则(S,*,0)和(S,Δ,0)都是半群.

记ES为半群(S,*,0)的幂等元集合.

定理8设(S,*,Δ,0)是一个N(2,2,0)-代数，若∀x∈S,x*x=0成立，则(S,*,0)是一个BRK-代数.

证明若∀x∈S，x*x=0⟹x*0=x*(x*x)=(x*x)*x=0*x=x，则(B8)成立；

又若∀x,y∈S，x*x=0， 则

(x*y)*x=(x*y)*(x*0)=x*((x*y)*0)=x*(x*y)=(x*x)*y=0*y，

因此(B9)成立.于是(S,*,0)是一个BRK-代数.

由文献[12]中定理1.2.9和定理1.2.10不难看出，一个BRK-代数不一定是N(2,2,0)-代数，但一个幂零的N(2,2,0)代数一定是BRK-代数.

定义11设(S,*,Δ,0)是一个N(2,2,0)代数，对于S的任意一个子集Q，定义

T(Q)={x∈Q|x*0=x}.

特殊地，如果Q=S，则称T(Q)是一个N(2,2,0)代数的T-部分.

定理9设(S,*,Δ,0)是一个N(2,2,0)代数，若∀x∈S,x*x=0 成立，则在T(S)中右消去律成立.

证明∀a,b,c∈T(S)，满足a*c=b*c，则由定理7知，∀a∈S,a*a=0⟹a*0=a，于是

a*c=b*c⟹a*c*c=b*c*c⟹a*0=b*0⟹a=b.

定理10设(S,*,Δ,0)是一个N(2,2,0)代数，若∀x∈S,x*x=0 成立，则(T(S),*,0)是一个阿贝尔群.

证明在(T(S),*,0)中，∀x,y∈T(S), 则

x*y=x*(y*0)=y*(x*0)=y*x，

于是0是(T(S),*,0)的一个单位元，由文献[13]中定理1.2.11知,T(S)的每一个元素都是自身的逆元, 因此(T(S),*,0)是一个阿贝尔群.

4 N(2,2,0)代数的理想与滤子

在一个N(2,2,0)-代数(S,*,Δ,0)中，称集合

G(S)={x∈S|x*0=0}

为S的一个p-根.

如果G(S)={0}，则称N(2,2,0)-代数(S,*,Δ,0)的半群(S,*,0)是p-半单的.

根据N(2,2,0)-代数的性质易知，若N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)是一个交换半群，则该半群(S,*,0)是p-半单的.

可以证明:G(S)⊆ES.事实上,有

∀x∈G(S)⟹x*0=0⟹(x*0)*x=0*x⟹x*(0*x)=x⟹x*x=x⟹x∈ES，

于是G(S)⊆ES.

显然，G(S)∩T(S)={0}.

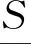
定义13设(S,*,Δ,0)是一个N(2,2,0)代数，A是S的一个非空子集，称A为S的一个理想，如果满足：

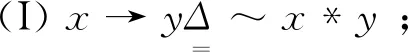
(II)x∈A，x*y∈A⟹y∈A.

定义14设(S,*,Δ,0)是一个N(2,2,0)代数，F是S的一个非空子集，称F为S的一个滤子，如果满足：

(I) 0∈F；

(II)x*y∈A,y∈A⟹x∈A.

定理11在N(2,2,0)-代数(S,*,Δ,0)中，G(S)={x|x*0=0}既是S的子代数，也是S的理想和滤子.

证明(1) 显然0∈G(S)，∀x,y∈G(S)，则

x*0=0,y*0=0⟹(x*0)*(y*0)=0⟹y*((x*0)*0)=

0⟹y*(x*0)=0⟹(y*x)*0=0⟹y*x∈G(S)，

类似可得x*y∈G(S)，因此G(S)是S的一个子代数.

(2) 显然0∈G(S)，∀x,y∈G(S)，x∈G(S)， 则

因此G(S)为S的一个理想.

类似可证G(S)为S的一个滤子.

在N(2,2,0)-代数(S,*,Δ,0)的子代数G(S)上定义一个关系“～G”如下

∀x,y∈G(S),x～Gy⟺(x*y)*0=0.

定理12在N(2,2,0)-代数(S,*,Δ,0)的G(S)={x|x*0=0}上，如果∀x∈G(S),x*x=0成立，则关系“～G”是G(S)上的一个等价关系.

证明(1) 由x*x=0⟹(x*x)*0=0⟹x～Gx，于是关系“～G”满足自反性.

(2) 由(x*y)*0=0⟹x*(y*0)=0⟹y*(x*0)=0⟹(y*x)*0=0，于是关系“～G”满足对称性.

(3) 若x～Gy,y～Gz，则

(x*y)*0=0,(y*z)*0=0⟹((x*y)*0)*((y*z)*0)=0*0=0，

即

((x*y)*(y*z))*0=0⟹(x*(y*y)*z)*0=0⟹(x*0*z)*0=0⟹(x*z)*0=0，

于是x～Gz，从而关系“～G”满足传递性.

因此，关系“～G”是G(S)上的一个等价关系.

设∀x,y,z,t∈G(S)，假定x～Gy,z～Gt，则

因此，关系“～G”是G(S)上的一个同余关系.

将x所在的等价类记为

规定

[x]*[y]=[x*y],[x]Δ[y]=[xΔy]，

则有定理13.