金诚杰 王昊 陈峻

摘要：通过课堂实验进行博弈论教学，能够有效促进学生对知识的理解。但在以往的实践中，此类实验通常只进行一次，效果不够显著。因此尝试在连续几周的课堂上开展博弈论实验，并在每次实验之间讲解前一次实验结果，对学生进行集体训练。连续实验结果表明，第一次实验不可能达到纳什均衡点，但在三周实验之后，学生的集体选择会逐渐接近均衡点，并且如果继续重复下去，最终可以达到目标。这一过程有效地强化了学生对博弈论原理的认识。同时通过博弈论知识的学习，交通专业的学生也进一步加深了对交通分配中Wardrop第一和第二原理本质的理解。

关键词：博弈论;课堂实验;纳什均衡;Wardrop原理

中图分类号：G642.0     文献标志码：A     文章编号：1674-9324（2020）15-0378-04

一、引言

博弈论是研究理性人互动的理论。1928年，冯-诺依曼证明了博弈论的基本原理，宣告了博弈论的诞生。1944年，他和摩根斯坦合著的《博弈论与经济行为》将二人博弈的情况推广到多人博弈结构，并且将博弈论系统应用于经济领域，奠定了这一学科的理论体系。在1950年，纳什用不动点定理证明了均衡点的存在，为博弈论的一般化奠定了基础。到今天，博弈论已经成为社会科学的通用方法论，对于理解各种社会现象具有非常重要的价值[1]。

为此，我国高校中很多专业都开展了博弈论知识的教学。由于博弈论的数学模型非常复杂，公式和符号抽象，学生通常不易理解，因此近年来很多学者开始在传统课堂讲授的基础上，引入博弈论实验的手段[2-6]。这种互动的教学模式更加有趣，有利于学生理解博弈的基本思想，也有助于活跃课堂气氛和提高教学效率，是值得广泛推广的。但在以往的博弈论课堂实验中[2-6]，基本上都只进行了一次实验，内容过于简单。有些学者在期末考试中引入了实验内容[7]，它的效果也等同于单次实验。事实上在一学期的连续多周课程里，完全有条件开展连续多次的重复课堂实验，从而更深入地揭示博弈论原理，进一步强化学习效果。因此我们针对这一点展开了尝试，取得了较好的效果，具体过程将在下文详述。

二、第1轮实验：初尝试

我们设计的实验内容如下：

在0—100之间选取一个数字，当所有学生的数字收上来之后，计算所有数字的平均数。选取数字最接近大家平均数2/3的学生是赢家，可以得到10元钱奖励。如果有多个赢家，则每人都有10元钱奖励。你将如何选择这个数字？

实验说明：

1.共有42名实验参与者，均为东南大学交通学院一年级研究生，大部分学生专业为交通运输规划与管理，少数为道路、载运、ITS等专业，均无相关实验经验，也从未学习过博弈论知识。

2.实验时间为15分钟，在实验过程中不允许和别人交谈，也不允许上网查找资料，完全独立完成。

3.参与者在白纸上写上自己的姓名，学号，选择的数字和理由。

这一实验内容和文献[6][7]描述的实验基本一致，主要区别在于文献[7]在期末考试中进行，将实验内容设定为试题，而文献[6]中要求为“数字最接近大家平均数1/2的学生是赢家”。在这次实验过程中，学生非常投入，很多人在时间结束时仍然在反复思考和推算。实验结束后，学生们对这个实验表达出了强烈的兴趣，例如下课时有学生表示希望能当场统计，当场出结果。

课后我们将42名学生的结果进行统计分析，按照每10个数为1个区间的方式进行划分，结果如表1所示。由于没有学生填写80以上的数字，所以表格中的最大区间为（71，80]。在42个数字中，最小值为0，最大值为75，平均值为28.53，它的2/3为19.02。由于无人选择19，所以最终赢家为2名选择20的学生。

这一实验存在着纳什均衡点0或者1，具体的分析和推导过程可参见文献[6]，本文不再赘述。此处主要讨论实验中发现的一些现象：

1.67以上的选择肯定是非理性的，因为即便平均值为100，它的2/3也只有66.7。本次实验中仍然有一名学生填写了75，并且说理由是“我喜欢”，可以看到即便对于一年级的工科研究生而言，仍然有少数人不具备基本的理性思维能力。

2.有的学生虽然给出了理论上可能的数值，但理由很不充分，事实上他们并未进行合理的分析。例如一名学生填写了61，理由是“我觉得大部分人会往黄金分割点靠近”。还有学生填写了50或40，理由是“我猜的”。

3.一些学生努力地进行了推理演绎，并且接近了最终的答案。例如在42人中，有多达10名学生选择了22，其中有代表性的理由是：

“如果没有假设条件，平均分布的结果应该是50，则50*2/3=33。可能大家都会想到这一角度，所以答案平均值会接近于33，则2/3应该为33*2/3=22”。

4.也有学生在22的基础上进一步演绎，继续乘以2/3，并得到了14或者15的结果。但即便是考虑到了“无限循环”的情况，他们也并未选择更小的数字（本次实验中无人选择1—10的数字）。

5.总共有2名学生选择了0，他们分析出了纳什均衡点，意识到在“无限循环”后，确实结果会趋向于0。但在这次实验中，写0事实上是一种非理性行为，因为如果大多数人未考虑到这一步的话，平均值必然远大于0，写0的人根本不可能成为最后的赢家。

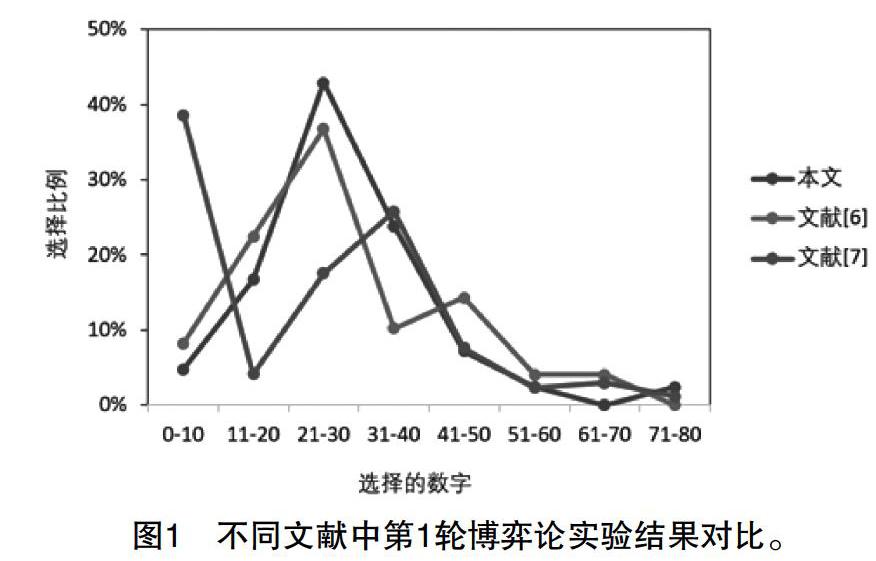
此处还可以将本文的实验结果与前人的实验结果进行对比。我们采集了文獻[6]和[7]的统计数据，并呈现在图1中作比较。可以看到当选择的数字较大（N>30）时，3次实验的结果非常接近，尤其是N>50时几乎完全一样。在数字较小时，本文结果和文献[6]的结果仍然基本一致，但文献[7]呈现出不同的状态，明显有较多学生选择了0-10这一区间，即更为接近纳什均衡点。另外从平均数而言，本文实验的结果为19.0，也明显大于文献[7]中的平均数14.6。

通过分析学生背景，可以发现文献[7]中的实验参与者是选修课逻辑与科学方法基础的学生，并且这一实验是期末考试中的一道题。此门课程的教师曾经以讲座的形式给他们讲授过博弈论知识，所以他们经历过一定的训练，具备了更强的思维能力。而本文和文献[6]的实验参与者，在实验前并未系统学习过博弈论，相对而言思维能力较弱，所以能考虑到纳什均衡点的学生明显较少。

三、第2轮实验：训练的效果

如前文所述，第1轮实验过程事实上与文献[6][7]几乎一样，并无多少创新之处。为了进一步加强学生对博弈论的理解，教师决定接下来进行更多更深入的实验。

首先，在第2周的课堂上，教师对第1轮实验的结果进行了介绍，包括公布了选择不同区间的人数比例和最终平均值，并且向学生具体分析了实验原理，指出选择0是纳什均衡点，但事实上在第1次实验中选0不可能成为赢家等等。此时学生开始对博弈论有了基本的认识，初步具备了策略性思维的能力，并且学习兴趣得到了进一步加强。

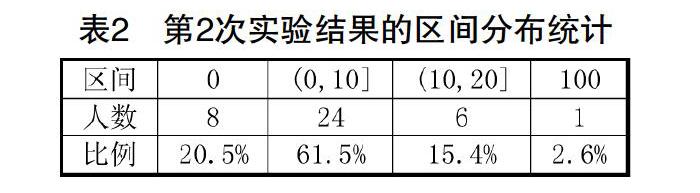
然后，教师立即在课堂上开展了第2轮实验，并且实验内容、过程和第1轮完全一样。但因为参加实验的学生经过了一次训练和学习，效果必然会有所不同。这次实验的结果如图2所示■，可以看到在了解了原理之后，大家的选择普遍更接近于0，平均值比第1次实验小了很多，并且有更多的学生（8名）直接选择了纳什均衡点。其中有2名学生在选择理由中直接指出，所有人选择0会导致系统最优，即“这样每个人都是赢家，每个人都可以获得10元钱奖励”。但与此同时，仍然有很多人考虑到“参与者不可能绝对理性，不可能大家都选0”，所以大多数学生（24名）选择了1—10之间的数字，并且有少数人（6名）选择了11—20之间的数字。这种对他人的普遍怀疑导致第2轮实验仍然没有出现系统最优的结果，平均值最终为7.76，2/3结果为5.17，最终赢家为2名选择5的学生。

值得一提的是，这次实验中有一名学生选择了数字100，并且在理由中写道：“反正我拿到钱的概率很小（或者说没有概率），就来做个不理性的破坏者吧。”由于他在平时是一个做事认真细心、守规矩、学习成绩比较好的学生，做出这样的行为可以说是令人意外的。但其实在生活中，我们也经常能观察到类似于“损人不利己”的非理性行为;一个人在分析过形势之后，感觉自己完全没有胜算，于是选择和对手“同归于尽”，道理上也算是说得通。这一情形充分体现出博弈论的一些基本假设、例如假设“参与者是绝对理性的”往往与事实不符，这一点和前人研究结论[1，7]一致。可以说我们的实验结果也是复杂人性的一次鲜活的体现。

四、第3轮实验：接近纳什均衡点

在第3周的课堂上，教师首先对第2周的实验结果进行了介绍，公布了选择不同区间的人数比例和最终平均值，并对大家的选择做了进一步分析。学生们对实验结果同样非常感兴趣，并且针对这轮实验中有人故意选择100的意外情况展开了热烈的讨论。

然后，教师在课堂上开展了第3轮实验，并且实验内容、过程和第1第2轮完全一样。此时学生们已经意识到，这个实验的最佳策略是所有人合作，全部选择0，这样所有人都是赢家，所有人都可以获得10块钱奖励。但同时，由于“前车之鉴”的存在，大家也会担心是否又有人搞破坏。在这两项因素的综合作用下，这次实验的结果比上一次更加接近于纳什均衡点，但并没有达到。具体结果如表3所示，这次的平均值为3.67，2/3结果为1.97，最终赢家为4名选择2的学生。

在第3次实验中，虽然有几名学生在写理由时谈到可能会有人搞破坏，甚至有学生预测说“这轮一定有更多的人捣乱，我猜应该有5—6个人”，但最后并没有出现这种情形：这次的最大值只有16，并且选择（11，20]的人只有2名。事实上正如另一名学生所预测的那样，“本次会有更多的人写得更小，搞破坏的人在一次之后会觉得无聊，不会增加多少”。

总的来说，通过这次实验我们可以观察到，系统在逐渐向纳什均衡点靠近，但这个靠近速度是很慢的。例如选择0的学生数量只从8增加到了10，并且有4名上一轮选择0的学生基于对整体的判断，这次反而选择了略大一些的数字。另外，已经有很多学生逐渐意识到了多轮重复实验的意义所在，例如有学生在理由中分析到“想问的是，到底要经历多少次实验才会实现共赢呢”。

五、未进行的下一轮实验：最后的讨论

在第4周的课堂上，同样地，教师首先对第3周的实验结果进行了介绍，公布了选择不同区间的人数比例和最终平均值，并对大家的选择做了进一步分析。虽然学生仍然对实验本身有兴趣，但对于是否还要继续重复相同实验，已经有些争议。事实上在第3次实验的结果中，已经有不止一名学生写到“对实验失去兴趣”或者“无法分析”。

显然，当学生对实验内容失去兴趣时，这个实验就无法再促进教学了。因此这次课上，教师先请学生们针对“是否要继续做第4轮实验”举手表决，结果发现大约80%的学生都认为没必要再做，并且大家普遍相信，假如继续做下去最终必然会达到纳什均衡点，所有人都会写0。唯一的悬念是还需要几轮才能达到，但这一轮数似乎并不重要。到此时，博弈论实验可以说圆满结束了：通过连续4周的学习和讨论，学生亲身体验了决策过程，在与集体的互动中深刻领会了博弈论的含义与乐趣，实现了较好的教学效果。

六、与交通工程知识的联系：以Wardrop原理为例

前文所述的几次博弈论实验，虽然非常有意义，但和交通工程领域并无直接联系。对于交通运输规划与管理的学生而言，还需要学以致用，能够将博弈论知识用于自己的专业领域。事实上很多交通问题都属于博弈论的范畴，只是由于交通参与者通常数量较多，往往难以使用博弈论直接求解。但使用博弈论的思维方式，仍然可以解释一些交通现象，加深学生的理解和认识。

此处我们以交通分配中的Wardrop原理为例，进行简单的诠释。Wardrop第一原理认为，网络上的交通分布结果，会使得所有使用的路线都比没有使用的路线费用小。Wardrop第二原理認为，车辆在网络上的分布，使得网络上所有车辆的总出行时间最小。如果交通分配模型满足Wardrop第一、第二原理，则该模型为平衡模型，并且满足第一原理的模型称为使用者优化平衡模型（User—Optimized Equilibrium），满足第二原理的模型称为系统优化平衡模型（System—Optimized Equilibrium）。如果模型不满足这两条原理，而是采用了模拟方法，则被称为非平衡模型。

交通工程教科书上[8]会指出，非平衡模型在实际工程中得到了广泛应用，效果良好，但却没有具体说明为何平衡模型使用效果不佳，为何Wardrop原理经常失效，导致学生往往并不明白其中原因。但如果结合博弈论和纳什均衡，则可以给出解释：

Wardrop第一原理基于用户的理性假设，认为用户总是尽可能地最小化自己的通行时间，所有的用户都如此选择的结果形成了用户均衡。Wardrop第二原理假设用户是合作的，最终使得系统总的通行时间最少。然而从纳什均衡的结果来看，Wardrop第一和第二原理之间根本不存在关联性，并且很多时候恰好相反：当所有用户试图满足Wardrop第一原理时，经常导致Wardrop第二原理得不到满足，系统的总时间会变大。这在著名的“囚徒困境”中有充分的体现：每个囚徒都会选择坦白，从而导致所有人都坐牢更长时间。而在我们的课堂实验中，会有很多学生在认真思考后仍然选择较大的数字，从而提升整体平均值，延缓系统达到均衡点的速度。更特殊的是，在少数时候，用户甚至不满足Wardrop第一原理：例如在我们的课堂實验中有学生故意选择100，干扰大家的结果。另外即便有教师指导，在大家经过3轮的集体学习和训练之后，仍然只是接近、而未达到系统均衡点，换言之系统的收敛速度没有之前想象中快。由此可以看出，要想在现实中让交通分配结果同时满足第一和第二原理，根本是不可能的，这也就是非平衡模型更实用的原因。

当我们在课堂教学中分析了这一点之后，学生普遍感觉到了学习博弈论对解决交通问题的帮助，同时也对交通分配方法和Wardrop原理有了更深刻的认识。

七、结论

为了提升教学效果，克服单次实验的缺陷，本文通过开展连续多次的课堂实验进行博弈论教学。结果表明，第一次博弈论实验不可能达到纳什均衡点，但在三周实验之后，学生的集体选择会逐渐接近均衡点，并且如果继续重复下去，最终可以达到。通过这一系列的实验，学生充分地了解了博弈论的基本原理，亲身体会了决策过程，学习兴趣得到了充分的激发。另外通过博弈论知识的学习，交通专业的学生也加深了对交通分配中Wardrop第一和第二原理本质的理解。在今后的教学实践中，我们计划针对更多的学生开展类似的实验，比较各次实验结果之间的相同点和不同点，进一步促进学生对博弈论和相关知识的理解和掌握。

注释：

（1）由于少数学生请假和旷课的缘故，第2次实验只有39名学生参加，第3次实验有40名学生参加，但这种差异对实验结果的影响基本可以忽略不计.

（2）为保护隐私，选择100的学生姓名并未公布，大家只是知道班里有一个人做出了这样的行为.

参考文献：

[1]刘晓丽.博弈实验对博弈论的方法论意义[J].学术探索，2013，（3）：24-28.

[2]李军军，黄茂兴.课堂实验在理论经济学教学中的应用与创新[J].福建师范大学学报：自然科学版，2011，27（3）：110-113.

[3]李太龙.博弈论公选课的教学内容与方法探析[J].教育探索，2012，（1）：42-44.

[4]乔磊.实验教学在经济学课堂教学中的应用[J].教育教学论坛，2012，（7）：218-219.

[5]李攀艺，周伍阳.经管类本科专业博弈论课程教学探悉[J].科教导刊-电子版（中旬（，2014，（7）：59.

[6]王新辉，黄莺，彭怡.博弈论策略性思维的课堂教学实现[J].西南民族大学学报：自然科学版，2015，41（3）：345-34.

[7]刘晓丽.从博弈实验看博弈论作为社会科学方法论的局限性[J].东南大学学报：哲学社会科学版，2012，14（4）：20-22.

[8]王炜，过秀成，等.交通工程学[M].南京：东南大学出版社，2003.