陈 龙，黄天立

(中南大学土木工程学院，湖南，长沙 410075)

在钢筋混凝土桥梁的服役过程中，常常受到服役恶劣环境侵蚀、材料自然老化、车辆荷载作用、维护措施不当等因素的影响，其服役性能随时间不断退化[1—2]。针对服役的钢筋混凝土桥梁，管理部门通常制定有定期的检测、评估计划，并根据检测结果评定桥梁的服役状态，进而制定相应的维修措施[2]，以确保桥梁结构的长寿命安全运营。因此，如何基于检测数据评估在役桥梁的安全性能，并根据评估结果准确地预测桥梁未来的服役状态，已成为世界各国桥梁工程界研究的热点问题之一。

采用合理的数学模型准确描述在役桥梁的抗力退化过程，是进行桥梁性能评估的前提和核心问题。国内外学者多采用仅考虑混凝土碳化、钢筋锈蚀等单一损伤因素的确定性衰减函数描述钢筋混凝土桥梁的性能退化过程[3—7]。此外，抗力退化过程受到多种因素影响且各影响因素之间相互耦合，导致抗力退化过程实质上属于一种非平稳随机过程，如采用确定性的衰减函数对退化过程进行描述，将有可能产生难以接受的分析误差[8]。

研究表明[9]，结构因磨损、疲劳、腐蚀、裂纹扩展、侵蚀、消耗、蠕变等原因产生的抗力退化本质上是一种累积损伤过程，并且有着不确定性、难以量化等特点。因此，为了更好地描述抗力退化过程中的不确定性和时间变异性，有研究学者引入具有独立增量性质的随机过程来描述退化过程，如维纳过程(Wiener process)和伽马过程(Gamma process)是最常采用的两种描述结构性能退化的随机过程[9—13]。基于伽马随机过程的退化模型，因其独立、非负增量的特性和对性能退化随机性和变异性的良好的适应性，近年来多被用于钢筋混凝土构件的退化建模。黄天立等[10—11]采用伽马过程描述了钢筋混凝土的纵筋锈蚀退化和钢结构疲劳裂缝长度增长随机过程。Strauss等[12]采用伽马随机过程描述了预应力混凝土在长期运营过程中出现的徐变收缩问题。Li等[13]以基于伽马随机过程的抗力退化模型为基础，建立了在役结构的时变可靠度的分析框架。

应该指出，一个合理的随机退化模型，既要考虑退化机制，还要考虑能够将实时监测信息融入模型，在退化机制决定退化函数整体形状的基础上，实时监测信息的融入可以减少原退化机制模型的不确定性。因此，描述抗力退化过程采取的随机过程模型应能够结合实时监测的结构退化信息，开展相应的更新工作，以得到与结构实际退化状态更匹配的退化模型。

最近，Wang和 Xu[14]提出逆高斯过程(Inverse Gaussian Process，IGP)可用于描述结构的性能退化过程。Peng等[15]采用逆高斯过程描述结构的性能退化，建立了一种基于贝叶斯分析融入实时监测结构退化信息，更新逆高斯随机退化过程模型的理论框架。Zhang等[16]借助逆高斯过程，建立了基于检测数据的地下能源管道腐蚀缺陷深度增长特征模型，并利用层次贝叶斯，考虑了不同信息来源的不确定性。

本文分别采用逆高斯随机过程和复合泊松过程建立桥梁抗力退化和车辆荷载效应模型，建立了基于抗力-荷载效应双随机过程模型的桥梁构件时变可靠度分析方法，推导了相应的时变可靠度计算公式。进一步，结合检测数据，采用贝叶斯分析和期望最大化(Expectation Maximization，EM)算法，对基于逆高斯过程的抗力退化模型参数进行更新，提出了在役钢筋混凝土桥梁构件可靠度的动态预测方法。以一座钢筋混凝土 T梁桥为例，采用其40 年服役期的抗力退化数据，分别在服役时间为18年、26年、34年和40年四个时刻对基于逆高斯过程的抗力退化模型参数进行了更新，演示了基于贝叶斯更新逆高斯随机抗力退化过程的桥梁可靠度动态预测方法。

1 抗力退化模型

1.1 逆高斯随机过程

假设随机变量 Y服从逆高斯分布，即y ～ IG(a,b)，参数 a、b均为正数，分别为分布的位置和形状参数，其均值为a，方差为a3/b，其概率密度函数(PDF)为：

其累计分布函数(CDF)为：式中，Φ[·]为标准正态分布的累计分布函数。图1给出了参数 a、b不同取值时逆高斯分布的概率密度函数。从图1中可以看出，位置参数a描述了分布峰值大致位置；形状参数b描述了数据分布的离散程度，b值越大，数据分布越分散，反之，数据分布越集中。

图1 参数a、b不同取值时逆高斯分布的概率密度函数Fig.1 The probability density functions of inverse Gaussiandistribution with different parameter values a and b

若随机过程{Y(t);t ＞ 0 }满足以下三个条件，则该随机过程为逆高斯过程：

1) Y(0)=0；

2) Y(t)是独立增量过程；

3) 增量ΔY(t)服从逆高斯分布，记作

式中： I G(μ ΔΛ,λ ΔΛ2)表示均值参数为μ，方差参数为λ的逆高斯分布； Δ Y (t) = Y (t + Δt )-Y(t)；ΔΛ ( t) = Λ ( t + Δt ) - Λ (t)；Λ(t)为形状函数，是一个非负的右连续非递减函数，且Λ(0)=0。当Λ(t)为线性函数时，逆高斯过程为平稳随机过程；当Λ(t)为非线性函数时，对应的逆高斯过程为非平稳随机过程。图2给出了简单逆高斯过程的15条演化曲线，其中μ=0.5，λ=0.5， Λ (t ) =t2。从图2中可以看出，对于所描述的随机过程{Y(t);t ＞ 0 }，其演化过程具有明显的随机性，每条演化曲线表示一种特定的演化路径。在给定阈值的情况下，变量t服从某个特定的概率分布，图2显示了阈值 Y (t) = 4 0时变量t的概率密度函数。

图2 简单逆高斯过程演化曲线Fig.2 The evolution curves of a simple inverse Gaussian process

1.2 基于逆高斯随机过程的抗力退化模型

由于恶劣环境和车辆荷载的作用，服役桥梁的服役性能总是不断退化，其抗力R(t)总是随时间递减。目前，通常采用抗力系数G(t)描述结构的退化状态进行，在特定时刻t，结构的抗力为：

式中：R0为初始抗力；G(t)为t时刻的抗力系数，当不考虑维修时，抗力系数总是从1开始单调递减。相应地，1-G(t)表示截止至t时刻时，抗力系数的累积退化量。

抗力系数G(t)可采用确定性函数来描述，如Mori和Ellingwood[7]提出的幂函数抗力系数：

式中，θ和q为表征幂函数形状参数。应该指出，幂函数形式的退化模型只适用于结构退化总体趋势受环境影响的退化过程。实际上，不仅限于幂函数，任何只要满足非增性质并能够较好描述结构因特定因素产生的退化现象的函数，均可作用于描述退化过程的基本函数。

应该指出，由于钢筋混凝土桥梁结构抗力退化过程具有不确定性和难以量化的特点，利用确定性函数表示退化过程并不合适。Wang和Xu[14]指出，逆高斯过程可用于建模结构在随机环境下的退化过程。考虑到结构退化本质是一种微小损伤的累积过程，因此，本文采用具有独立、非负退化增量的逆高斯随机过程描述抗力系数累积退化量Ys(t) = 1 - G (t )。

针对桥梁结构的退化总体趋势受环境影响，本文采用van Noortwijk和Klatter[17]建议的幂函数形状函数，即 Λ ( t) = tq。此时，描述抗力系数累积退化量的逆高斯过程为， Ys(t) ～ IG[ μ Λ(t ) , λ Λ2(t )]，μ,λ ＞ 0 。其概率密度函数为：

表1给出了钢筋混凝土结构不同退化类型情况下指数参数q的取值。在结构退化检测数据足够多的情况下，直接通过统计分析获得q的取值，是最合适的方法。然而，由于土木工程结构服役周期长，相应的抗力退化监测数据不足，难以完全基于统计分析获取q的取值。van Noortwijk和Klatter[17]指出，在对退化过程具有足够工程认知的前提下，指数参数q的取值可采用常数，并且该常数值可根据所考虑的退化过程适当调整。因此，本文在对检测数据进行拟合的基础上，综合工程经验，适当调整了指数参数q的取值，参数μ、λ的估计及更新方法见第4节。

表1 不同退化类型情况下指数参数q的取值Table 1 Values of the exponential parameter q of different degradation types

2 基于复合泊松过程的车载模型

桥梁结构承受的荷载主要包括恒载和活载两部分，其中恒载由桥梁自重产生，且通常认为恒载基本不随时间变化。本文将恒载H视为服从正态分布的随机变量[18]，即 H ～ N (1 . 0418Gk,0.0437Gk)，Gk为恒载标准值。

一般情况下，桥梁活载主要考虑车辆荷载，其本质上属于非平稳随机过程。文献[18]指出，密集分布的车辆荷载出现在桥梁上的持续时间非常短，而且出现的时间间隔可以认为服从指数分布，因此，本文车辆荷载采用复合泊松过程描述。根据复合泊松过程模型，在任一时间长度区间τ内，通过车辆荷载的次数N()τ为n次的概率为[19]：

式中：n = 0 ,1,2,3,4…；γ为单位时间内车辆荷载发生的次数，即到达率。对桥梁进行可靠度分析时，主要关心产生最不利荷载效应的荷载组合。假设在时间段τ内出现n次最不利荷载Sj(j=1,2,…,n)，且Sj服从同一分布类型，且相互独立，其分布函数取为时间长度区间τ内相应的最大概率分布函数Fsj(s)，如图3所示。本文采用极值Ⅰ型分布来研究桥梁的荷载效应[18]。

图3 基于抗力-荷载双随机过程的时变可靠度计算模型Fig.3 Calculation models for time-dependent reliability of bridges using resistance and load effect stochastic process

3 时变可靠度计算

分别采用逆高斯过程和复合泊松过程描述桥梁抗力退化过程和车辆荷载效应，基于抗力-荷载双随机过程，结合式(3)定义结构的功能函数 Z （t）为：

式中：S(t)为车辆荷载；G(t)为抗力退化系数；H为恒载。由此得到t时刻结构的瞬时失效概率为：

当不考虑初始抗力R0和恒载H的随机性时，由式(8)卷积积分计算得到瞬时失效概率：

假设桥梁抗力和荷载效应相互独立，则式(9)可表示为：

对z进行积分：

式中：fs(s;t)为活载的概率密度函数； fG(t)(y;t)和FG(t)(y;t)分别表示抗力系数G(t)的概率密度函数和累积分布函数。特别说明，抗力系数G(t)的随机分布由抗力系数累积退化量[1-G(t)]服从逆高斯分布确定，即：

由于式(12)积分式的上下限都是无穷，特别在后文考虑抗力和恒载的随机性时，数值积分较为困难，因此本文首先对其进行参数变换[20]，即令u = FG(t)(y;t )，则 y ∈ (-∞ ,+∞ )等效于u∈(0,1)，使其积分上下限变为(0,1)，由此，瞬时失效概率可由式(14)计算：为推导相关的可靠度计算公式，引入危险函数概念[13]，其定义为结构在[0,t]时间范围内没有失效的条件下，在[t,t+dt]时间范围内的失效概率，危险函数h(t)与可靠度函数R(t)之间的关系为：

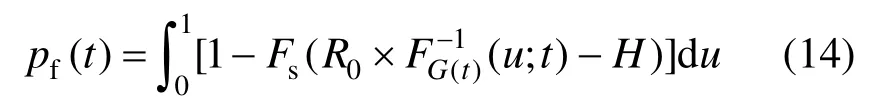
若已知危险函数，则结构可靠度函数为：

假设在时间范围[0,T]内，在时刻t1,t2,t3,… tn上出现n个独立的最不利荷载事件如图3所示，此时危险函数h(t)可表示为：

式中：Tf为结构失效时间随机变量；P(t ≤ Tf≤ t + dt )表示结构在时间范围[t,t+dt]内的失效概率； P (Tf≤t)表示结构直到时刻t都不会失效的概率。如前所述，最不利荷载Sj出现的次数服从泊松过程，根据泊松过程的相关性质可得：

将式(18)代入式(17)可得：

则时变可靠度函数表示为：

当考虑初始抗力R0和恒载H的随机性时，时变可靠度函数为：

4 基于贝叶斯更新和逆高斯过程的可靠度动态预测

近年来，随机过程因对不确定问题的良好适用性而被广泛应用于钢筋锈蚀、钢结构疲劳、磨耗等退化问题的随机建模。然而，研究工作主要集中在对退化过程初始模型的参数估计[10—11,13]，很少结合实时监测获得的数据对模型参数进行更新。本节采用桥梁服役过程中获取的承载力检测评估数据，联合贝叶斯分析和期望最大化算法，建立了针对逆高斯过程抗力退化模型参数估计的更新方法，进而给出了基于贝叶斯更新和逆高斯过程的在役钢筋混凝土桥梁构件动态可靠度预测方法的框架流程。

4.1 基于Bayesian更新和EM算法的逆高斯过程模型参数估计

如前所述，逆高斯过程抗力退化模型中包含三个参数μ、λ和q，其中指数参数q可通过拟合实际检测数据和工程经验共同确定，而退化参数μ和λ需根据实际检测数据进行统计分析确定。研究表明[21]，对于特定退化系统，基于随机系数回归模型建模监测数据，意味着退化路径的确定化；若在获得退化监测数据后，通过 Bayesian更新，可以对模型的随机参数进行后验估计。但是，对于退化模型中非随机的未知参数，仅依靠单一路径数据无法进行标定。均值参数对于退化轨迹的期望值有很大影响，而方差参数只刻画退化过程的不确定性。因此，本文采用基于Bayesian更新与EM算法的模型参数估计方法对退化模型进行更新[21—22]，其中将均值参数μ视为随机参数，方差参数λ视为非随机参数。

假设某钢筋混凝土桥梁在其服役时间段内有连续的检测时间点1,2,3,in记ttt…t…t，每个时间点对应的退化数据记为，代表到时刻tk的退化数据集。设为时刻ti-1到ti的退化增量，对随机参数μ采用贝叶斯后验估计，在给定参数μ的情况下，退化数据集的联合分布为：

首先，假设随机参数1/μ的先验分布服从正态分布 N (α,β2) ，由贝叶斯理论可知1/μ的后验分布为：

由式(24)、式(25)可知1/μ的后验分布也服从正态分布族，如式(26)、式(27)所示，因此参数1/μ的共轭先验分布是正态分布，其先验分布的选取是合理的。

由于随机参数μ为含有隐变量的随机变量，无法采用极大似然估计，本文采用EM算法进行估计。EM 算法的标准计算框架由期望步(Expectation step，E-step)和最大化步(Maximization step，M-step)交替组成。在期望步构建针对隐变量的对数似然函数，然后再取期望。

将模型参数记为 Ω = ( α,β2,λ)，由EM算法第j次迭代产生的模型参数估计结果为(α(j), β2(j),λ(j))，若1/μ可观测，则有对数似然函数：

4.2 基于贝叶斯更新和逆高斯过程的动态可靠度预测

依照上述参数估计方法，本文旨在结合桥梁在服役过程中的检测数据，构建一种桥梁构件可靠度动态分析框架，能够准确地预测桥梁的剩余使用寿命。其主要流程分三大部分：

1) 获取检测数据，对桥梁进行抗力评定，收集抗力系数数据集

2) 结合收集的检测数据，利用贝叶斯和EM算法对逆高斯抗力退化模型进行实时更新。

3) 联系荷载模型，通过式(23)进行时变可靠度分析，并对桥梁构件的剩余寿命进行预测。

综上分析，图5给出了基于贝叶斯更新和逆高斯过程的在役钢筋混凝土桥梁构件可靠度动态预测流程图。

图4 基于Bayesian更新与EM算法的逆高斯过程模型参数估计流程图Fig.4 Flowchart for estimating parameters of inverse Gaussian process model using Bayesian updating and EM algorithm

图5 基于贝叶斯更新和逆高斯过程的在役钢筋混凝土桥梁构件可靠度动态预测流程图Fig.5 Flowchart of the dynamic prediction procedure for reliability of existing RC bridge members using Bayesianupdating and inverse Gaussian process (IGP)

5 算例分析

某钢筋混凝土T型梁桥建于1966年，共6跨，计算跨径为15 m，其跨中截面如图6所示，本文对其中一根T梁跨中截面的抗弯承载力进行可靠度分析和预测。载效应的随机性。初始抗弯承载力 R0=1 703 k N·m，恒载效应 H = 3 57.1 kN·m ，设计使用年限T=100

图6 某T梁桥跨中截面 /cm Fig.6 Mid-span cross-section of a T-girder bridge

针对T梁跨中截面弯矩承载力，本文不考虑初始抗力和恒载的随机性，仅考虑抗力退化和车辆荷年内最大车辆荷载效应为均值 4 34.2 kN·m ，标准γ= 1，年均最大车辆荷载效应均值为189.21 kN·m。

桥梁构件抗力随服役时间增加而逐渐退化，由于该桥修建年代较早，没有完整的连续性的抗力退化检测数据。为验证所提方法的可行性，本文采用文献[23]的桥梁确定性抗力退化模型，假设该T梁桥每两年检测一次，首先每间隔两年生成一系列抗力退化系数数据，然后在这些数据中加入10%的随机误差(考虑桥梁构件抗力退化过程的随机性)，最终得到一系列模拟的抗力退化系数数据，当作该T梁桥的实际检测数据，如图7所示。

基于图7所示该T梁40年服役期的抗力退化数据，采用本文提出的逆高斯过程抗力退化模型，可以模拟得到构件在剩余年限内的退化过程。在桥梁服役t=34年后，图8给出了基于逆高斯过程抗力退化模型模拟得到的15条抗力退化系数演化曲线。图9给出了抗力系数累积退化量[1-G(t)]的概率密度函数随时间的变化规律。

融入桥梁服役期间获得的结构退化信息，对桥梁构件可靠度进行分析和动态预测，可更为准确地差68.12 kN·m的极值 I型分布，单位时间到达率评估构件的现状，预测其未来服役状态，进而更准确地估计桥梁构件的剩余使用寿命。

图7 T梁桥40年服役期抗力退化系数数据Fig.7 Degradation data of a T-girder bridge in 40 years

图8 基于逆高斯过程的抗力系数演化曲线Fig.8 The simulated resistance coefficient evolution curves using the IGP

图9 抗力系数累积退化量的概率密度函数Fig.9 The probability density function of the cumulative degradation loss of resistance coefficient

针对此服役40年的钢筋混凝土T型梁桥，采用获得的服役期抗力退化数据，分别选择在四个时间点(即服役期分别为18年、26年、34年和40年时)，根据图4给出的基于Bayesian更新与EM算法的逆高斯过程模型参数估计流程，分别获得此四个时刻更新的逆高斯过程抗力退化模型参数，如表2所示。从表2中可以看出，随桥梁服役时间增加，指数参数q从1.0增加到2.0，这主要是考虑到钢筋混凝土中钢筋锈蚀产生锈胀裂缝将加速钢筋混凝土桥梁的抗力退化的工程经验，并结合实际检测的抗力退化数据综合确定的。

表2 更新的逆高斯过程抗力退化模型参数Table 2 Updated parameters of the IGP-based resistance degradation model

基于图5的流程图，预测得到该T梁分别在服役期为18年、26年、34年和40年时的失效概率曲线，如图 10所示，图中横坐标表示从预测的服役时刻开始，再继续服役的年限。从图 10中可以看出，随桥梁服役时间增加，T梁的失效概率不断增大。当设定T梁的目标失效概率为 1 × 1 0-6时，分别根据服役期为18年、26年时预测得到的失效概率曲线，可判定该T梁桥满足设计使用寿命100年的要求；分别根据服役期为34年、40年时预测得到的失效概率曲线，可推断该T梁桥再服役48年、40年失效，即该T梁桥的预期使用寿命分别为82年、80年，不满足设计使用寿命100年的要求。

对比图10所示服役期为18年、26年时预测的失效概率曲线和服役期为34年、40年预测的失效概率曲线可知，前两条曲线与后两条曲线的上升速率不同，这与影响钢筋混凝土桥梁退化的主要因素不同有关。在钢筋混凝土梁桥服役前期，其性能退化的主要因素是混凝土碳化和钢筋锈蚀，钢筋锈蚀还没有在混凝土表面产生锈胀裂缝，由此检测的抗力退化信息中不包含裂缝对桥梁的影响，因此，在服役期为18年、26年时预测得到失效概率曲线上升速率较小。随着钢筋混凝土梁桥服役时间增长，混凝土表面出现锈胀裂缝，裂缝的出现将加快钢筋锈蚀，从而引起结构抗力的加速退化，因此，在服役期为34年、40年时预测得到失效概率曲线上升速率较大。对比服役期为26年、34年时预测的失效概率曲线，发现两条曲线的上升速率差别较大。从抗力退化模型分析，主要是由于服役期为 26年和 34年时预测失效概率曲线所采用的指数参数 q取值不同，其取值分别为1.5和2.0。从混凝土结构退化机理来说，可能是由于锈胀裂缝的出现时间刚好在服役期为26年至34年之间，由于锈胀裂缝的出现，各种混凝土退化因素相互影响，共同作用，加剧了桥梁的损伤，导致了桥梁抗力退化速率的突变。

图10 不同服役时刻预测的T梁桥失效概率曲线Fig.10 The predicted failure probability curves of the T-girder bridge at four different service time

6 结论

(1) 针对确定性退化模型无法准确描述钢筋混凝土桥梁构件抗力退化过程不确定性和时间变异性的不足，引入逆高斯随机过程描述其抗力退化过程，同时采用复合泊松过程描述车辆荷载效应，建立了基于抗力-车辆荷载效应双随机过程的在役钢筋混凝土桥梁构件时变可靠度分析方法。结合检测数据，采用贝叶斯分析和期望最大化算法，对逆高斯过程抗力退化模型参数进行更新，提出了在役钢筋混凝土桥梁可靠度的动态预测方法。

(2) 以一座钢筋混凝土T梁桥为例，采用其40年服役期抗力退化数据，分别在服役时间为18年、26年、34年和40年四个时刻对基于逆高斯过程的抗力退化模型参数进行了更新，演示了提出的可靠度动态预测方法，预测了这四个服役时刻该T梁桥的失效概率曲线。算例结果表明：给定桥梁失效概率目标值时，基于服役期为18年、26年时预测的可靠度判定该T梁桥满足设计使用寿命100年的要求；而基于服役期为34年、40年时预测的可靠度判定该T梁桥的预期使用寿命分别为82年、80年，不满足设计使用寿命100年的要求。

(3) 逆高斯随机过程可更合理地描述钢筋混凝土桥梁构件抗力退化过程中的不确定性和时间变异性；融入桥梁服役期间的退化数据后，可更准确地预测桥梁构件未来的可靠度服役状况和估计桥梁的剩余使用寿命。

(4) 针对钢筋混凝土桥梁的性能退化，本文采用的是简单幂函数形式抗力退化模型，可进一步考虑从材料的退化机理出发，采用考虑锈蚀、开裂等影响因素的抗力退化模型，则研究结论将更符合钢筋混凝土桥梁的实际。