姚 忠，陈超倩，王 瑞，徐保成

(西北机电工程研究所，陕西咸阳 712099)

0 引言

现代海战的节奏不断加快，海战对抗强度空前加剧，这对舰炮火控系统实时性与精确性提出了更高的要求[1]。诸元解算是火控系统的核心任务之一，求解方法主要有射表法与外弹道法。但射表法严重依赖射表数据，且解算精度不高，算法的通用性较差，设计过程繁杂，已无法满足现代海战对火控系统的要求。随着现代计算机技术的发展，运算速度及存储能力不断提升，为了最大限度提升火控系统性能，外弹道实时解算必将成为今后的发展趋势。

国内外学者已对外弹道数值解算开展了一系列研究。现行解算方法中，较为典型的是引入二分法求根思想，求解火炮外弹道方程组决定射击诸元[2-3]。此外，遗传算法(GA)、粒子群算法(PSO)等智能优化算法也逐渐引入弹道解算中，如刘彦君[4]基于改进的GA，动态缩小搜索区域，对诸元求解问题进行了研究；崔静等[5]提出了一种基于改进的PSO算法与周氏迭代修正公式的外弹道解算方法，减小了弹道解算时间。万有引力搜索算法(GSA)是由Rashedi于2009年首次提出，研究表明，GSA算法在收敛性及全局优化能力方面均优于GA与PSO[6-12]。因此，文中将GSA算法引入舰炮射击诸元解算求解中，以提高诸元解算的实时性，缩短解算周期。

1 外弹道模型及解命中算法

1.1 外弹道模型

外弹道模型是射击诸元解算的基础，当前常用的两类外弹道模型为质点弹道模型与刚体弹道模型。文中以某型舰载火炮为例，采用后者建立弹丸外弹道模型如式(1)所示[13]。

(1)

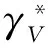
1.2 解命中算法

由于弹丸外弹道模型是基于地面坐标系进行积分，因此解命中问题亦选在地面坐标系进行求解。同时，忽略延时时间、基线修正等因素，给出解命中问题方程组如下：

(2)

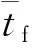
解命中问题的本质即是求解式(2)，一般采用迭代法对其进行求解。为了提高收敛速度，并扩大收敛区域，引入弦截法求解该式[14-15]。

设S(j)为待定的迭代权系数，可得弹丸飞行时间与目标运动时间之间的迭代关系为：

(3)

(4)

I(A)为特征值参数，其物理意义为命中点的目标距变率与弹丸末速度的比值。

(5)

(6)

2 基于GSA算法的射击诸元解算

将GSA算法引入射击诸元解算问题中[6-7]，则诸元解算可看做一定射角约束条件下的二维优化问题：

minf(α)

(7)

式中:f(α)为目标函数，其物理意义为弹着点与目标提前点的距离；α为由高低角α1与方向角α2构成的二维决策向量。

GSA算法采用粒子的空间位置表示待优化问题的解，第i个粒子的空间位置定义为：

(8)

在t时刻，第j个粒子对第i个粒子的引力作用表示为：

(9)

式中:d=1,2为空间维度；Mi(t)与Mj(t)为粒子的惯性质量；Rij(t)=‖αi(t),αj(t)‖2为两个粒子间的欧式距离；G(t)为t时刻的引力常数，定义如下:

G(t)=G0exp(-λn/nmax)

(10)

式中:G0为引力常数初值；λ为引力常数的衰减速率；n为当前迭代数；nmax为迭代总数。

t时刻第i个粒子在d维上的合力为：

(11)

式中：N为粒子数量；k-best表示种群中质量较大的粒子，且随t线性衰减，使算法在搜索空间中仅有代表最优解的粒子去作用其余粒子；randj为[0,1]间的随机数。

GSA算法中用适应度函数值来表示粒子的惯性质量，显然惯性质量越大，粒子的引力越强，运动越慢，优化问题有更优的解。粒子惯性质量根据适应度的计算为：

(12)

(13)

式中，fitnessi(t)为适应值，通过外弹道解算获得；best(t)与worst(t)定义如下:

(14)

(15)

根据牛顿第二运动定律给出粒子i在第d维上的加速度为：

(16)

(17)

(18)

此外，为提高射角的收敛速度，利用弹道刚性原理[16]对初始射角进行预估，并在初始射角附近随机生成N个粒子。根据上述原理，可以得到基于GSA的射击诸元解算流程见图1。

图1 射击诸元解算流程

3 仿真分析

根据前文建立的基于GSA算法的舰炮射击诸元解算模型，以某大口径舰炮为研究对象，在标准条件下对该算法进行仿真分析，并与文献[3]中基于二分法的诸元解算方法进行对比验证。

选取弹丸直径为d、质量为m、气动阻力系数按照43年阻力定律获取、重力加速度为9.8 m/s2。假设目标沿某条航路作匀速直线运动，运动速度v=[0 0 17.5]T，单位m/s，初始位置坐标为M0=[10 0]T，单位km。

为选取合适的引力常数初值G0及引力常数衰减速率λ，需分析以上两个参数对解算精度的影响。GSA算法中，种群数量为35，分别改变G0与λ，得到弹着点偏差变化曲线如图2、图3所示。

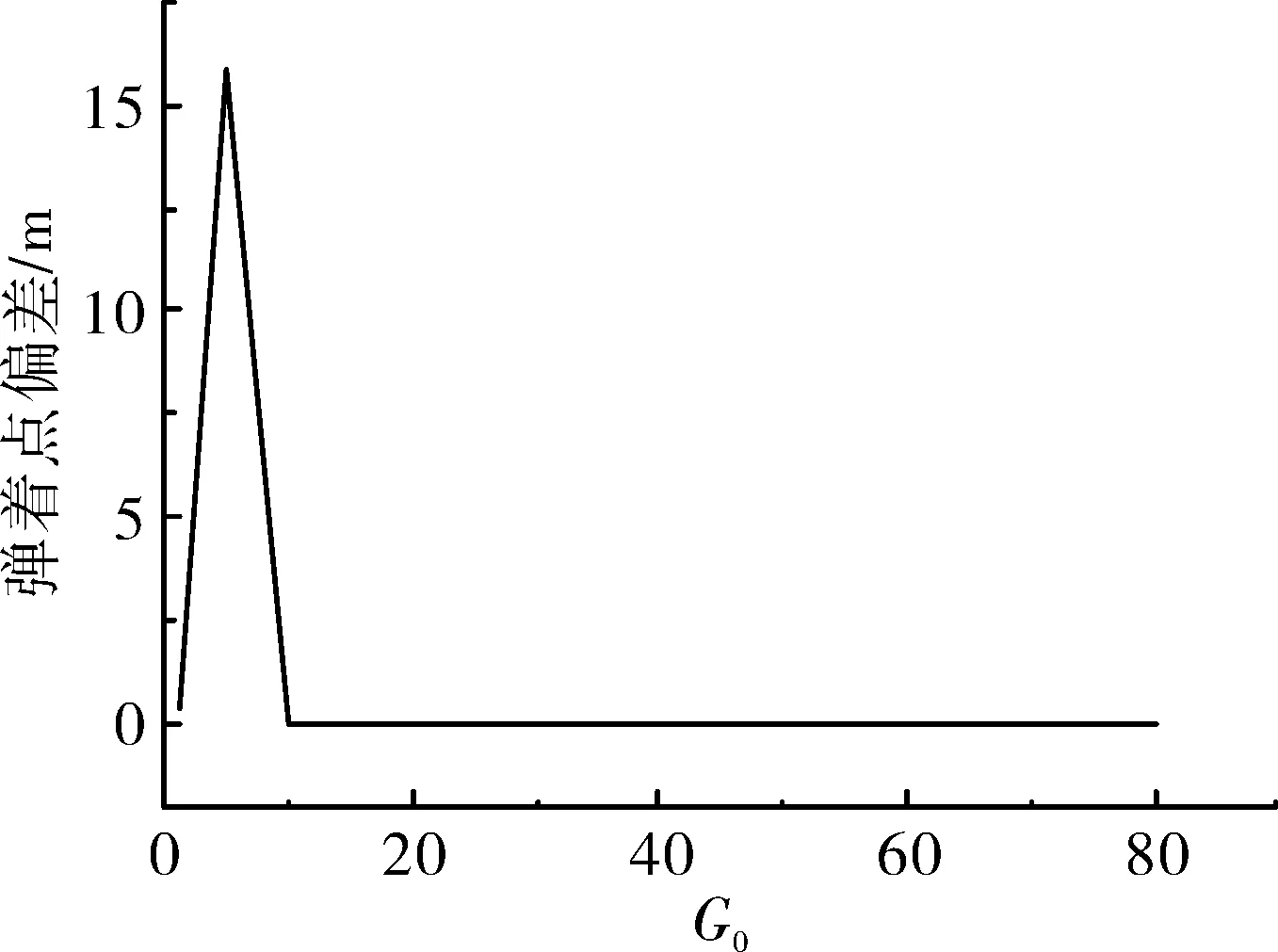
图2 弹着点偏差随G0变化曲线

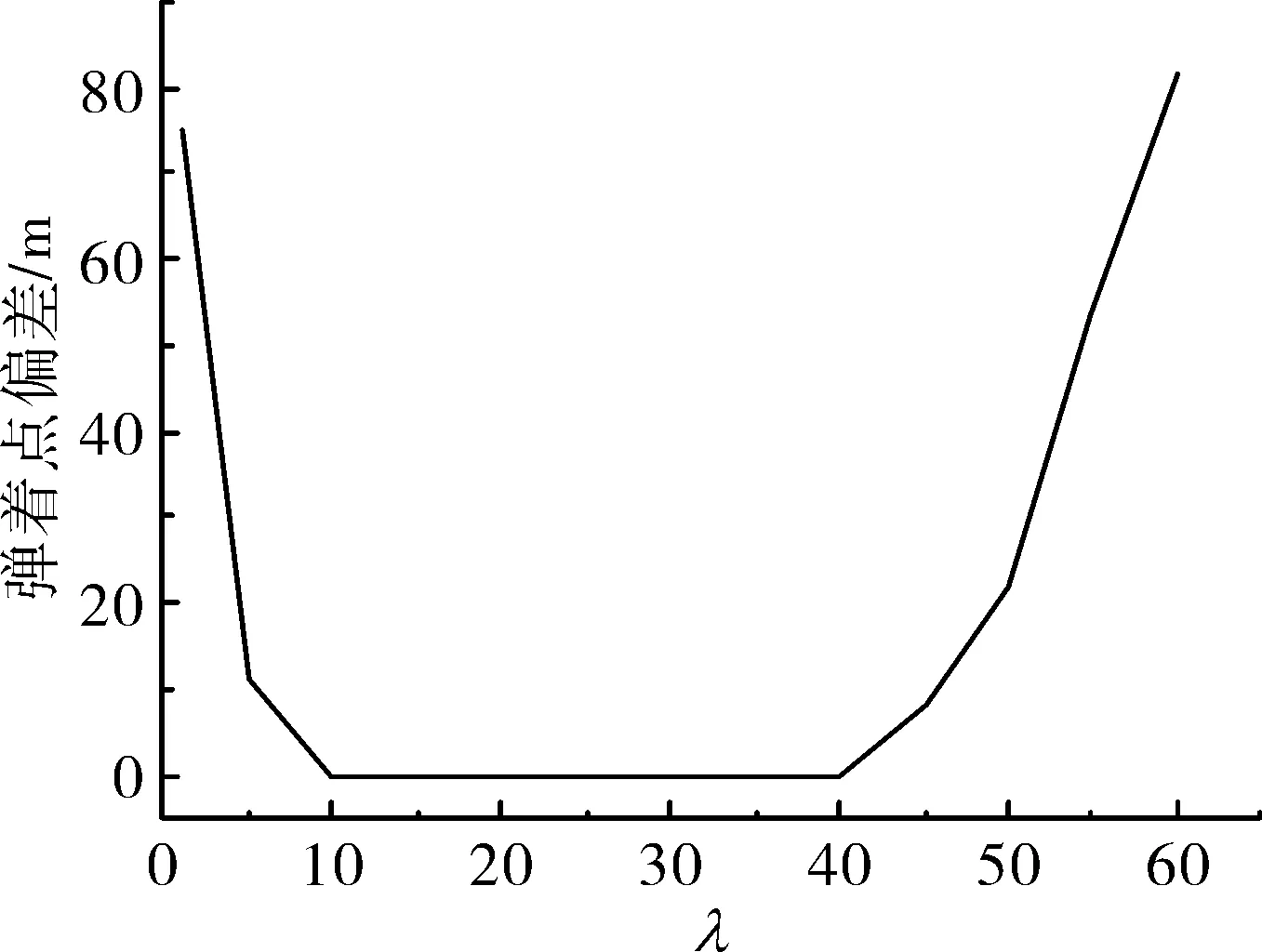
图3 弹着点偏差随λ变化曲线

从图2可以看出，随着引力常数初值G0逐渐增大，弹着点偏差在G0约为5时达到峰值，随后迅速降低至10-5量级，并持续保持稳定；同时，由图3可知，弹着点偏差随引力常数衰减速率λ的不断增大，呈现先减小后增大的U型趋势，当λ取值处于10～40之间时，偏差达到10-3量级。

通过多次仿真实验，综合G0与λ对弹着点偏差的影响，同时考虑尽量减少解算时间，选取G0=26，λ=15。

采用上述算法参数，针对基于二分法与GSA的两种解算方法分别进行仿真，得到表1所示的射击诸元解算结果。

通过对表1仿真结果的分析可以看出，文中采用的基于GSA算法的诸元解算方法在保证解算精度的同时，所消耗的解算时间明显小于现行的二分法。这是由于弹道刚性原理的引入大幅缩小了射角的搜索范围。与此同时，GSA算法中各粒子具有相互独立性，可充分发挥计算机多核并行计算的优势，有效提高计算效率，缩短解算周期。

表1 射击诸元解算结果对比

4 结论

通过对GSA算法在舰炮射击诸元求解问题方面的应用研究，得到以下结论：

1)引入GSA算法，提出了一种新型舰炮射击诸元求解算法，仿真结果表明了该算法的正确性与有效性；

2)与现行诸元解算方法相比，文中提出的算法具有较好的通用性，在保证计算精度的同时，有效提高了解算效率，解算周期明显缩短，具有更好的实时性。